感知机、梯队下降、激活函数、损失函数
神经网络语言模型(NNLM)涉及的概念
神经网络语言模型(NNLM),通过神经网络训练语言模型可以得到词向量。
1. 感知机
感知机就是一个将两类物体分开的一条直线(一个超平面)。我们将一些参数输进感知机,感知机就能告诉我这个点属于“芝士”还是“巧克力”。在机器学习中,这样的点称为“数据”,而各个维度的坐标大小称之为“特征”。而可以对点分类的感知机就是神经网络的一个神经元。
例如,确定给二维世界原住民分类的方案,并且知道怎么来使得随着数据的输入让模型变得越来越接近真实情况。而这种模型就叫感知机模型。
而感知机有一个非常明显的特征——它是线性的,只能分辨出一条直线两边各一种蛋糕。这儿先来给出一个结论: 线性模型不可分类异或问题。
我们知道二维世界的每个人都具有一个标签,就像身份证一样,那就是它们的坐标。假设你给它们分类的时候不是直接在里面画一条直线,直线一侧的是一类,另一侧的是另一类;而是以它们的(x,y)(x,y)坐标值来分类,xx,yy值相同的为一类,不同的为另一类,那么小C还能用上面的方法分类吗?显然是不可能的,而这个问题就属于异或问题,异或问题就属于线性不可分问题。
现在我们知道用感知机来解决分类问题是有限制的,也就是不能解决线性不可分问题,因此在应用感知机模型之前需要判断该问题是否是线性不可分的。
那么遇到非线性可分的数据集又会怎么办呢?例如,在四拼蛋糕中,分辨出你想要的巧克力蛋糕,一个感知机显然是不够的,这个时候就需要多个感知机一起来工作。
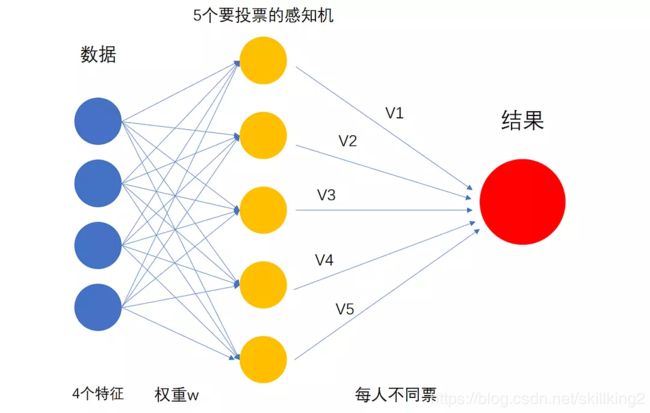
如果这群感知机的数量足够多而且每个感知机的想法都不太一样,将它们结合到一起,就能够找到最适合的结果。由于感知机的分辨能力各不相同,分辨能力越强的感知机判断结果所占的权重也越大。V1~V5就是五位感知机手里的票数,也就是它们的权重,将他们的结果按照权重加起来,再和0比较(扔进sign函数),就可以分辨出你想要的蛋糕了。在机器学习中,这种通过构建并结合多个学习器来完成学习的方法叫“集合学习(Aggregation)”。这种多个感知机集合在一起做投票的模型就是神经网络,数据输入的一列神经元称为输入层(Input Layer),中间的神经元属于是隐藏层(Hidden Layer),而最后输出结果的则是输出层(Output Layer)。
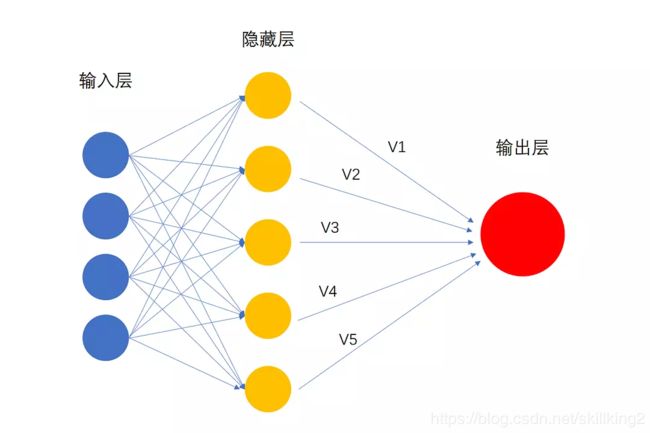
神经网络的每一层的神经元数量都可以改变的,隐藏层中神经元数量增加的会让神经网络的学习能力变得更强大,如果输出层不只有一个神经元,那么这个神经网络就可以做多元分类,如下图输出层有两个神经元的神经网络,就可以输出[1 1],[1 -1],[-1 1],[-1 -1]四种可能,那么就可以做四元分类了。
实际上,在神经网络中我们不用sign函数,因为sign函数没有办法做微分,这会对我们优化神经网络时造成极大的困难,一般来说我们在神经网络中使用的是可以微分的tanh函数(或者sigmoid函数)。
2、梯度下降法
怎么能让神经网络更快速的分辨蛋糕呢?这里介绍一种训练方法叫——梯度下降法。通过分配正确的权重给机智的感知机,让它们带领神经网络走向胜利。
以二维数据作为例子,这两维的权重是Θ0和Θ1,,我们将神经网络犯错的数量表达成一个函数J(损失函数Cost Function)。J越大,证明犯错越多,就像红色的山峰;J越小,证明犯错越少,例如蓝色的山脚所在点。在梯度下降中,不断地改变Θ0,Θ1的值,使得J(Θ0,Θ1)变小,直到找到J的最小值或许是局部最小值。
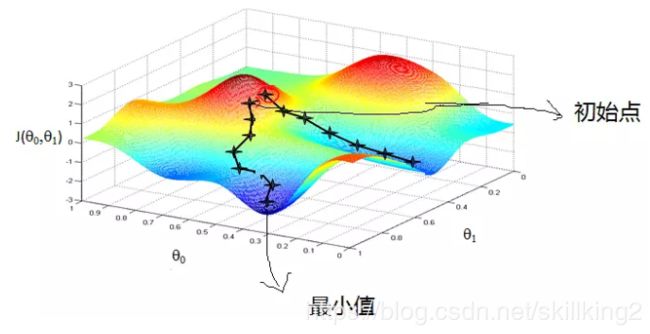
例如,我们要借助GPS下山,Θ0和Θ1对应的是经度和维度,而J则是高度,在安全的前提下,走越陡峭的路就能越快下山。下面我们介绍如何找这个最陡的方向,我们对J求每一个权重Θj的偏导数,即梯度
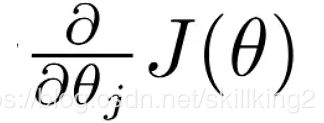
然后我们对在这个最陡的方向走α步,即
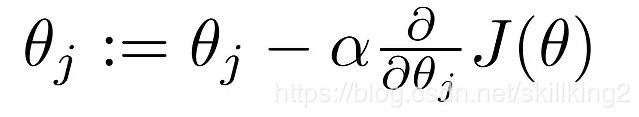
走完之后,停下来,找到新的最陡的方向,再走α步,一直到我们走到了山脚。
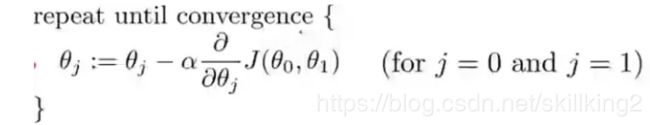
这样我们就找到了最优化的权重。
梯度下降法有时会陷入局部最优化的危险,但是大多数我们需要解决的问题大多都是局部最优化=全局最优化的,所以也并不需要太担心。
3. 深度神经网络
我们刚刚谈到,每一层的神经元数量是可以变化的,那么其实隐藏层的数量也是可以变化的,多隐藏层的神经网络其实就是深度神经网络。
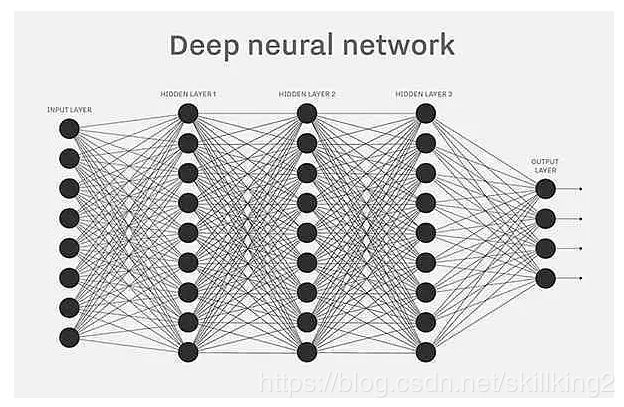
我们怎么去理解多层神经网络呢?就像在你的脑海里,经过一层又一层的筛选,最终找到最爱的那一块蛋糕。深度神经网络比浅层的神经网络具有更强的学习能力,能提供更复杂的模型,相比于浅层神经网络,深度神经网络能学到更多的“意义”。
越深层的神经网络,能够学习到更抽象的“概念”,比如狗狗、花、鸟等,浅层神经网络只懂得简单的线条,这证明了,深度神经网络才能够挑选出符合人工神经网络胃口的最终蛋糕。
但是深层的神经网络需要训练的时间更长,需要的数据量也更大,而且往往会陷入过拟合的危险中。所以如何训练出一个优秀的神经网络成为了众多工程师亟待解决的问题。
过拟合: 过拟合是机器学习专家们一直为之头痛的问题。过拟合的意思是模型在训练样本上做得太好了以至于实际用上的时候表现非常差。
对于解决过拟合的办法,我们往往会做正则化(Regularization)。举个例子,我们会在神经网络的损失函数J中加入regularizer,如Θ^2,去惩罚过于复杂的模型,避免过拟合。

3. 激活函数
所谓激活函数(Activation Function),就是在人工神经网络的神经元上运行的函数,负责将神经元的输入映射到输出端。
如果不用激励函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合,这种情况就是最原始的感知机(Perceptron)。
如果使用的话,激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。
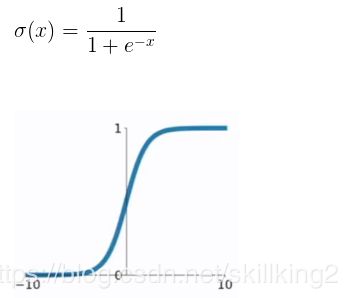
1).Sigmoid函数:
在sigmod函数中我们可以看到,其输出是在(0,1)这个开区间内,否则变量范围为(−∞,+∞ ), 不方便计算。这点很有意思,可以联想到概率,但是严格意义上讲,不要当成概率。sigmod函数曾经是比较流行的,它可以想象成一个神经元的放电率,在中间斜率比较大的地方是神经元的敏感区,在两边斜率很平缓的地方是神经元的抑制区。
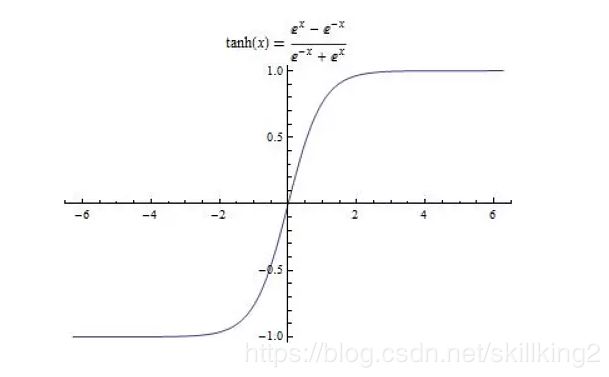
2).tanh函数
tanh是双曲正切函数,tanh函数和sigmod函数的曲线是比较相近的,咱们来比较一下看看。首先相同的是,这两个函数在输入很大或是很小的时候,输出都几乎平滑,梯度很小,不利于权重更新;不同的是输出区间,tanh的输出区间是在(-1,1)之间,而且整个函数是以0为中心的,这个特点比sigmod的好。
一般二分类问题中,隐藏层用tanh函数,输出层用sigmod函数。不过这些也都不是一成不变的,具体使用什么激活函数,还是要根据具体的问题来具体分析,还是要靠调试的。
3). softmax
Softmax函数,或称归一化指数函数,是逻辑函数的一种推广。它能将一个含任意实数的K维向量 Z “压缩”到另一个K维实向量 Θ(Z) 中,使得每一个元素的范围都在(0, 1)之间,并且所有元素的和为1。
4). sign函数
sign(x)或者Sign(x)叫做符号函数,在数学和计算机运算中,其功能是取某个数的符号(正或负):
当x>0,sign(x)=1;
当x=0,sign(x)=0;
当x<0, sign(x)=-1;
4. 损失函数
是用来估量你模型的预测值f(x)与真实值Y的不一致程度,它是一个非负实值函数,通常使用L(Y, f(x))来表示,损失函数越小,模型的鲁棒性就越好。
5. 平滑算法
在自然语言处理中,经常要计算单词序列(句子)出现的概率估计。我们知道,算法在训练时,语料库不可能包含所有可能出现的序列。因此,为了防止对训练样本中未出现的新序列概率估计值为零,人们发明了好多改善估计新序列出现概率的算法,即数据平滑算法。
本文参考并摘自
https://www.douban.com/note/647214569/
https://blog.csdn.net/yxhlfx/article/details/79093456