OpenCV4学习笔记(22)——轮廓发现
本次要记录的内容是轮廓的相关内容,由于内容比较杂乱,就一点一点地根据代码来整理吧。
- 轮廓发现:
Mat connected_image = imread("D:\\opencv_c++\\opencv_tutorial\\data\\images\\contours.png");
imshow("connected_image", connected_image);
Mat connected_image_gray;
cvtColor(connected_image, connected_image_gray, COLOR_BGR2GRAY);
Mat connected_image_gaus;
GaussianBlur(connected_image_gray, connected_image_gaus, Size(), 1, 1);
Mat connected_image_binary;
threshold(connected_image_gaus, connected_image_binary, 0, 255, THRESH_BINARY | THRESH_OTSU);
imshow("connected_image_binary", connected_image_binary);
vector<vector<Point>> contours;
vector<Vec4i> hierarchy;
findContours(connected_image_binary, contours, hierarchy, RETR_TREE, CHAIN_APPROX_SIMPLE, Point());
首先读入一张图像并进行预处理操作,包括转灰度图、高斯模糊去除噪声、二值化处理得到二值图像,然后就可以通过OpenCV中提供的寻找轮廓APIfindContours(connected_image_binary, contours, hierarchy, RETR_TREE, CHAIN_APPROX_SIMPLE, Point())来寻找二值图像中的轮廓,其参数解释如下:
第一个参数image:输入的需要寻找轮廓的二值图像;
第二个参数contours:获取的轮廓集合,每个轮廓是一系列轮廓上的点集合,使用vector来定义该参数;向量contours中的每个元素,都是一个轮廓,每个轮廓都是一个点向量;contours向量内每个元素保存了一组由连续的Point构成的点的集合的向量;
第三个参数hierarchy:轮廓层次信息的集合,每个轮廓的层次信息是一个Vec4i类型的元素,使用vector来定义该参数;每个轮廓的层次信息按顺序包括:同层下一个轮廓的索引、同层上一个轮廓的索引、下一层第一个子轮廓的索引(子节点)、父轮廓的索引(父节点);如果当前轮廓没有对应的同层下一个轮廓、同层上一个轮廓、父轮廓和下一层第一个子轮廓,则相应的hierarchy[i][*]被置为-1( * 取值为0~3);
第四个参数mode:表示输出的轮廓结构,常用的有:
(1)RETR_EXTERNAL:只输出最外层轮廓;
(2)RETR_TREE:输出轮廓树结构,也就是以树的形式输出所有轮廓;
(3)RETR_LIST:输出所有的轮廓,但每个轮廓相互独立,没有父子等级限制,所以hierarchy[i][2]和hierarchy[i][3]会被置为-1;
(4)RETR_CCOMP: 输出所有的轮廓,但所有轮廓只建立两个等级关系,外围为顶层,若外围内的内围轮廓还包含了其他的轮廓信息,则内围内的所有轮廓均归属于顶层;也就是说父层为顶层,子层为底层,子层的子层也为父层;
第五个参数method:表示获取轮廓点集合的不同算法,常见的是: CHAIN_APPROX_SIMPLE链式编码方法,仅保存轮廓的拐点信息,把所有轮廓拐点处的点保存入contours向量内,拐点与拐点之间直线段上的信息点不予保留;
第六个参数offset:所有的轮廓信息相对于原始图像对应点的偏移量,相当于在每一个检测出的轮廓点加上该偏移量,并且Point可以是负值。
到这里就实现了对图像中轮廓的发现。
- 轮廓绘制
接着我们就可以对找到的轮廓进行进一步操作,例如计算轮廓的面积和周长,并且绘制出轮廓,相关代码如下:
for (int i = 0; i < contours.size(); i++)
{
double contour_area = contourArea(contours[i], false);
double contour_length = arcLength(contours[i], true);
if (contour_area < 100 || contour_length < 100)
{
continue; //如果该轮廓面积或者长度小于100,则跳过该轮廓
}
//绘制轮廓
drawContours(connected_image, contours, i, Scalar(0, 255, 0), 1, 8);
}
首先通过for循环来遍历轮廓点集中的每一个轮廓,使用contourArea(contours[i], false)这个API来计算轮廓的面积,其返回值就是该轮廓的面积。其第一个参数是输入的需要计算的轮廓,第二个参数oriented是一个轮廓面向区域标识符,若为true,该函数返回一个带符号的面积值,其正负取决于轮廓的方向(构成轮廓的节点顺序是逆时针或顺时针),根据这个特性我们可以根据面积的符号来确定轮廓的位置,该参数有默认值false,表示面积以绝对值返回,不带符号。
在使用arcLength(contours[i], true)或计算轮廓的周长,其返回值就是该轮廓的周长,其第一个参数是输入轮廓,第二个参数closed是用于指示曲线是否封闭的标识符,为布尔类型,若为true则表示曲线封闭。
当获取了轮廓的面积和周长,就可以通过轮廓的面积与周长来实现对不同大小对象的过滤,寻找到感兴趣的ROI区域。随后就可以将保留下来的轮廓进行可视化绘制了,相关API是drawContours(connected_image, contours, i, Scalar(0, 255, 0), 1, 8),其参数解释如下:
第一个参数image:输入输出图像,表示在该图像上进行轮廓绘制;
第二个参数contours:需要绘制的轮廓集合;
第三个参数contoursIdx:要绘制的某个轮廓的索引,如果是负数就绘制所有轮廓;
第四个参数hierarchy:层次信息;只有绘制部分轮廓时才使用;
第五个参数maxLevel:绘制轮廓的最高级别,这个参数只在使用参数hierarchy时才生效;
若maxLevel=0,绘制与输入轮廓属于同一层次的所有轮廓即绘制输入轮廓和与其相邻的轮廓;
若maxLevel=1, 绘制与输入轮廓同一层次的所有轮廓与其下一层的第一个子轮廓(子节点);
若maxLevel=2,绘制与输入轮廓同一层次的所有轮廓与其下一层第一个子轮廓(子节点)以及子节点的子节点;
第六个参数offset:绘制的轮廓信息相对于原始图像对应点的偏移量,相当于在每一个绘制的轮廓点加上该偏移量,并且Point可以是负值。
通过遍历轮廓for循环,就可以将图像中寻找到的轮廓中符合面积和周长要求的逐个绘制出来。
- 轮廓外接矩形
轮廓外接矩形有很多个,其中重要的有最小外接正矩形和最小外接旋转矩形,这两种矩形包含了轮廓的某些信息。
其中最小外接正矩形可以用boundingRect(contours[i])这个API来实现,其输入参数array是一个输入轮廓,可以为包含轮廓点的向量(vector),计算完成后返回一个包含轮廓的最小外接正矩形,然后通过矩形绘制 API就可以将其可视化出来。
Rect max_rect = boundingRect(contours[i]);
rectangle(connected_image, max_rect, Scalar(0, 0, 255), 1, 8, 0);
最小外接旋转矩形是所有轮廓外接矩形中面积最小的一个,也叫最小外接矩形,可以使用minAreaRect(contours[i])来获取。其输入参数为需要求取最小外接旋转矩形的轮廓,然后返回一个RotatedRect类的对象,该类表示平面上的旋转矩形,该矩形的顶点坐标是浮点类型,需要使用Point2f来获取。
当获取了最小外接矩形的宽和高后,选择其中较小者除以其中较大者,就可以计算最小外接旋转矩形的横纵比,通过不同大小的横纵比可以来筛选或者过滤部分轮廓,减少干扰。
当需要绘制最小外接旋转矩阵时,需要获取其四个顶点和宽高,然后分别绘制四条直线来连接成一个封闭的矩形区域。rectangle()只适用于绘制正矩形,无法用来绘制旋转矩形。
RotatedRect min_rect = minAreaRect(contours[i]);
Point2f min_rect_4points[4];
min_rect.points(min_rect_4points); //获取最小外接斜矩形的四个顶点
int min_rect_width = min_rect.size.width;
int min_rect_height = min_rect.size.height;
float radio = min(min_rect_width, min_rect_height) / max(min_rect_width, min_rect_height);
for (int j = 0; j < 4; j++)
{
//对四个点依次连线形成矩形
//取余是为了将四个点连成封闭矩形
line(connected_image, min_rect_4points[j % 4], min_rect_4points[(j + 1) % 4], Scalar(255, 0, 0), 1, 8, 0);
}
Point2f min_rect_center = min_rect.center;
而且上述求得的最小外接正矩形和最小外接旋转矩形,它们都具有一个中心坐标,当时需要注意的是,这些中心坐标是外接矩形的中心坐标,而不是轮廓本身的质心坐标。
当我们需要获取轮廓本身的质心坐标时,需要先计算轮廓的几何矩,再通过输出的几何矩求取质心坐标,代码如下:
Moments moment;
moment = moments(contours[i]);
int cx = moment.m10 / moment.m00;
int cy = moment.m01 / moment.m00;
circle(connected_image, Point(cx, cy), 2, Scalar(0, 255, 255), -1, 8, 0);
通过moments(contours[i])来计算轮廓的几何距,其第一个参数是为输入的轮廓,第二个参数表示是否将输入图像进行二值化,默认值是false,该参数只在第一个参数为非二值图像时生效。
函数返回值是一个Moments对象,其中包含了轮廓的几何距(m…)、中心距(mu…)、归一化矩(nu…),可以通过轮廓的几何矩来求取轮廓的质心坐标,也就是使用x和y方向的两个一阶几何分别矩除以零阶几何矩。还可以根据几何矩输出结果来计算胡矩,这个后续再做整理。
这样就得到了我们需要的轮廓质心坐标。
- 轮廓拟合多边形
有时候需要知道轮廓的大致形状,就可以通过轮廓拟合多边形来进行粗略的判断。OpenCV中提供了approxPolyDP(contours[i], approxCurve, 4, true)这个API来进行轮廓拟合多边形,其参数解释如下:
第一个参数curve:输入的轮廓点集;
第二个参数approxCurve:输出的拟合多边形的顶点集,使用Mat对象来定义,每一行为拟合多边形的一个顶点坐标;
第三个参数epsilon:拟合的点集和输入点集的对应点之间的最大距离,该距离越小,越逼近真实轮廓;
第四个参数closed:若为true,则拟合形状是闭合的;若为false,则拟合形状是断开的。
进行多边形拟合后,就可以通过输出的approxCurve中包含的顶点数,也就是行数来判断拟合出的形状具有几个顶点、是几边形。假如输出结果有三行数据也就是三个顶点,那么轮廓大致为三角形;如果输出结果有四行数据也就是四个顶点,那么轮廓大致为矩形。具体代码如下:
Mat approxCurve;
approxPolyDP(contours[i], approxCurve, 4, true);
if (approxCurve.rows == 3) //输出的拟合多边形顶点集有三行,也就是三个顶点
{
putText(connected_image, "triangle", min_rect_center, FONT_HERSHEY_COMPLEX_SMALL, 0.6, Scalar(255, 255, 255), 1, 8, false);
}
if (approxCurve.rows > 10) //顶点数多于10,相当于圆形
{
putText(connected_image, "circle", min_rect_center, FONT_HERSHEY_COMPLEX_SMALL, 0.6, Scalar(255, 255, 255), 1, 8, false);
}
if (approxCurve.rows == 4) //4个顶点判断为矩形
{
putText(connected_image, "rectangle", min_rect_center, FONT_HERSHEY_COMPLEX_SMALL, 0.6, Scalar(255, 255, 255), 1, 8, false);
}
}
imshow("connected_image", connected_image);
本文中所有代码的运行效果如下:
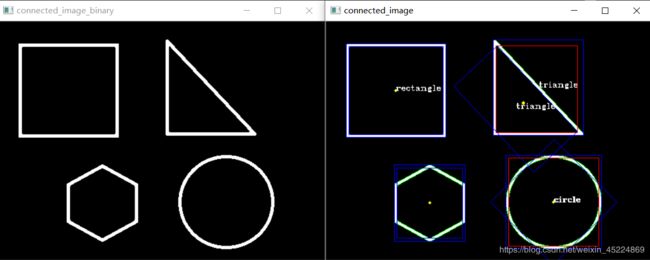
效果图中绘制了几何形状的轮廓、轮廓质心、内外轮廓的最小外接正矩形、最小外接旋转矩形,以及标识出了该轮廓的拟合多边形判断结果。
好的本次整理记录到此结束,感谢阅读~
PS:本人的注释比较杂,既有自己的心得体会也有网上查阅资料时摘抄下的知识内容,所以如有雷同,纯属我向前辈学习的致敬,如果有前辈觉得我的笔记内容侵犯了您的知识产权,请和我联系,我会将涉及到的博文内容删除,谢谢!