- 从 How 到 What:探索命令式与声明式编程的哲学
Vitalia
编程范式&语言艺术开发语言
编程范式是程序员用来构建程序的基本风格或方法。在众多编程范式中,命令式编程和声明式编程是最常见的两种。它们的主要区别在于程序员如何描述程序的逻辑和行为。文章目录命令式编程:指示程序如何改变状态1.过程式编程(ProceduralProgramming)2.面向对象编程(Object-orientedProgramming,OOP)特点示例声明式编程:只说结果,不说过程1.函数式编程(Functio
- vue 启动项目报错Cannot read properties of undefined (reading ‘parseComponent‘)
知道的越多越难受
vuevue.jsjavascript前端
如果出现如下报错大概率是因为install时中途出现异常导致vue-template-compiler依赖没有正常安装导致的,重新安装即可SyntaxError:TypeError:Cannotreadpropertiesofundefined(reading'parseComponent')Youmayusespecialcommentstodisablesomewarnings.Use//es
- Linux下使用poll函数编写UDP客户端、服务器程序
崔杰城
linuxudp网络协议网络
一、UDP服务器与客户端的区别对于UDP服务器与客户端,两者都可以通过sendto和recvfrom函数收发数据,它们的主要区别是:1.服务器一般是等待并响应来自客户端的请求,客户端则是主动发送请求并且等待服务器的响应。2.服务器端要将地址和端口号绑定,如果不绑定就无法使用recvfrom函数接受数据(也就是说服务器需要调用bind函数将一个套接字与一个地址绑定,而客户端不需要)。所以对于UDP,
- 非线性动力学笔记C2.1-2.2 一维流动中的不动点和稳定性
阿北Ben
笔记
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档文章目录前言C2一维流动(flowonaline)引言2.1几何思考方式2.不动点(fixedpoint)与稳定性(stability)Appendix1前言提示:这里可以添加本文要记录的大概内容:参考书《Nonlineardynamicsandchaos》StevenH.Strogatz本节重点Note第二章内容的引言的1-2小节,
- 每周论文精读05-A2J:AnchortoJointRegressionNetwork for 3D ArticulatedPoseEstimation from a SingleDepthImage
Jason_____Wang
精读笔记python计算机视觉卷积手势识别深度学习
https://download.csdn.net/download/Jason_____Wang/16502249论文精读——A2J:Anchor-to-JointRegressionNetworkfor3DArticulatedPoseEstimationfromaSingleDepthImage标题比较长,已经打不完了。。所以题目格式有些变形,望谅解。上周尝试做了一下代码复现的方向,因为生活
- k8s 中的 service 如何找到绑定的 Pod 以及如何实现 Pod 负载均衡
「已注销」
kubernetes负载均衡docker
前言Service资源主要用于为Pod对象提供一个固定、统一的访问接口及负载均衡的能力。service是一组具有相同labelpod集合的抽象,集群内外的各个服务可以通过service进行互相通信。当创建一个service对象时也会对应创建一个endpoint对象,endpoint是用来做容器发现的,service只是将多个pod进行关联,实际的路由转发都是由kubernetes中的kube-pr
- Leetcode 712. Minimum ASCII Delete Sum for Two Strings
小白菜又菜
Leetcode解题报告动态规划(DP)leetcode算法
ProblemGiventwostringss1ands2,returnthelowestASCIIsumofdeletedcharacterstomaketwostringsequal.AlgorithmDynamicProgramming(DP):similarasLongestCommonSubsequence(LCS).Ifs1[i]!=s2[j]:F(i,j)=min(F(i−1,j)
- Qt QComboBox 下拉列表偏移问题探究:多屏幕与高 DPI 环境下的 bug
吃面不喝汤66
Qtqtbug开发语言
一、问题背景与重现步骤现象描述:在Qt应用程序中,主界面包含QComboBox控件,并且启用了高DPI支持(例如在main()中调用QCoreApplication::setAttribute(Qt::AA_EnableHighDpiScaling))。当用户将窗口拖动到不同DPI的屏幕上,点击QComboBox弹出下拉列表时,下拉列表的位置与预期不符,出现明显偏移,从而影响用户体验。重现步骤:在
- Apache ZooKeeper 分布式协调服务
slovess
分布式apachezookeeper
1.ZooKeeper概述1.1定义与定位核心定位:分布式系统的协调服务,提供强一致性的配置管理、命名服务、分布式锁和集群管理能力核心模型:基于树形节点(ZNode)的键值存储,支持Watcher监听机制生态地位:Hadoop/Kafka等生态核心依赖,分布式系统基础设施级组件1.2设计目标强一致性:所有节点数据最终一致(基于ZAB协议)高可用性:集群半数以上节点存活即可提供服务顺序性:全局唯一递
- Android Preference隐藏,删除方式
码点
androidframworkAndroid底层知识androidjavaapache
在Android系统开发中,经常需要去掉或者隐藏原生设置的一些条目。一、隐藏Preference方法@VisibleForTestingstaticfinalStringENABLE="enable";Preferenceenable=findPreference(ENABLE);enable.setVisible(false);R.xml.main&l
- Ollama容器+打造DeepSeek-R1-7B大模型
码哝小鱼
AI大模型docker运维语言模型
1、获取Ollama官方镜像1.1在线拉取镜像#dokcerpullollama/ollama:0.5.71.2导入离线镜像#tar-zxfollama0.5.7_x86.tar.gz#dokcerload-iollama0.5.7.tar2、执行以下命令创建与启动ollama#dockerrun-dp8880:11434--nameollama\-eOLLAMA_HOST=0.0.0.0:114
- DPlayer + vue3 使用
是晓周哦
javascriptvue.js前端视频typescript
帮助文档https://dplayer.diygod.dev/zh/guide.html#special-thanks安装pnpminstalldplayer--savepnpminstall@types/dplayer--save-dev使用方法import{ref,onMounted,onBeforeUnmount}from'vue';importDPlayerfrom'dplayer';im
- qt UI架构之MVD
yaofei2006
ui架构
在Qt中,MVD(Model-View-Delegate)是一种用于分离数据、显示和用户交互的设计架构。它是MVC(Model-View-Controller)的变体,特别适合用于处理复杂的数据显示和编辑场景(如表格、列表、树形结构等)。1.MVD架构的核心组件MVD架构由以下三个核心组件组成:1.1Model(模型)负责管理数据。提供数据的访问接口(如data()和setData())。通知视图
- python M3U8转换为MP4
会飞的鱼—
python
importosimportasyncioimportrandomimportshutilimportaiohttpimportffmpegfromconcurrent.futuresimportThreadPoolExecutor#M3U8文件的URL#m3u8_url='********************.m3u8'#临时存储TS文件的文件夹ts_folder='ts_files'os.
- Springboot整合AWS s3 存储
宁漂打工仔
Java#AWSspringbootawsjava
依赖com.amazonawsaws-java-sdk-s31.11.543Awsyaml配置amazon:aws:access-key-id:AKIATaccess-key-secret:Tv7Cks3:default-bucket:region:endpoint:https://.com/Configimportcom.amazonaws.auth.AWSCredentials;importc
- [Ubuntu 20.04]Realtek ALC294无声音解决
CatTomCSDN
ubuntulinux
本文首发于本人博客:[Ubuntu20.04]RealtekALC294无声音解决目录环境问题解决附:查看你使用的声卡型号参考环境ASUSFL8000UUbuntu20.04问题RealtekALC294声卡在Ubuntu20.04下外放/耳机无声音估计这个问题应该只要是ASUS都可能会遇到,不论笔记本还是主板…解决修改/etc/modprobe.d/alsa-base.conf在文件的最后添加o
- Netty UDP 客户端发消息后接收服务器信息
一顿敲代码的小朋
nettyjava
在本站大神的文章的基础上,加入了我的项目需求,当客户端用UDP给服务端发送消息后,接收到服务端返回的消息再关闭客户端。UdpServer.javaimportio.netty.bootstrap.Bootstrap;importio.netty.channel.ChannelOption;importio.netty.channel.EventLoopGroup;importio.netty.ch
- i510300h和i78750h参数对比哪个好
妙龙
笔记本
i510300H是笔记本平台的标准电压处理器,为四核心八线程,主频2.5GHz,睿频4.5GHz,45WTDP,8M三级缓存,passmark跑分为9026分。我的笔记本就是活动时8折抢购的https://list.jd.com/list.html?i7-8750H的规格是6核心12线程,coffcelake架构,主频2.2GHz,单核最大睿频4.1GHz,六核最大睿频3.9GHz,L3缓存9MB
- Pinia入门
qincjun
前端学习指南pinia
一、铺垫pinia官网:https://pinia.vuejs.org/zh/getting-started.html以下的内容全部来自官网;只不过有时候访问官网上不去;只能自己扒下来;pinia的前端使用非常简单;只需要掌握几个步骤就可以二、套路1.用你喜欢的包管理器安装pinia:yarnaddpinia#或者使用npmnpminstallpinia2.创建一个pinia实例(根store)并
- 入手评测 i71165g7和i711390H选哪个好
m0_51380603
cpucpu
i711390H属于TigerLake-H35系列为4核心8线程,三缓12MB,不过基频更高,达到了3.39GHz,。i7-11390H单核睿频最高可达5GHz,TDP在28-35W之间选i711390h还是i71165g7这些点很重要http://www.adiannao.cn/dyi7-1165G7处理器相关参数:4核8线程,主频2.8GHz,睿频4.7GHz,12MB三级缓存。
- Java-数据结构-(TreeMap & TreeSet)
爱是小小的癌
Java数据结构数据结构算法java
一、搜索树①搜索树的概念搜索树是一种数据结构,用于高效的存储和查询数据,它通过树形结构组织数据,使得搜索、插入和删除操作的时间复杂度较低,这次我们来介绍比较常见的搜索树:"二叉搜索树"二叉搜索树的性质:有序性:对于树中的每个节点:左子树的所有节点值都小于该节点的值右子树的所有节点值都大于该节点的值它的左右子树也分别为二叉搜索树高效操作:搜索:比较目标值与当前节点值,决定向左或向右子树搜索,时间复杂
- wps配置deepseek
养码哥
wpsdeepseek
wps配置deepseekhttps://e6jy62bip4.feishu.cn/docx/R09IdpU5HoADyDxcgfQcjpR8nnb
- 找不到gpedit.msc 的解决方法
大写字母E
计算机配置window
通常打开本地组策略编辑器,只需要win+R在运行里输入gpedit.msc就可以打开。但是,在windows家庭版和学生版里,会提示找不到路径。可以用以下办法解决:新建一个文本文档,名字随便取,编辑以下批处理内容,保存后将后缀名改为.bat,右键使用管理员权限执行:@echooffpushd"%~dp0"dir/bC:\Windows\servicing\Packages\Microsoft-Wi
- 【cmd】Win10家庭版找不到 gpedit.msc (组策略)的解决方法
顾三殇
Win服务器部署/cmd命令组策略
目录一、创建cmd文件二、以“管理员身份”运行“gpedit.cmd”文件三、运行“gpedit.msc”命令查看组策略一、创建cmd文件(1)新建一个文件名为“gpedit.txt”的txt文本文档:(2)文本中写入以下内容:@echooffpushd"%~dp0"dir/bC:\Windows\servicing\Packages\Microsoft-Windows-GroupPolicy-C
- 找不到“本地策略”,没有“本地策略”的解决办法
Bawei_
windows
本文提供找不到本地策略的解决办法只需4步,结果如下图:1.首先打开记事本,并输入以下内容@echooffpushd“%~dp0”dir/b%systemroot%\Windows\servicing\Packages\Microsoft-Windows-GroupPolicy-ClientExtensions-Package~3*.mum>gp.txtdir/b%systemroot%\servi
- HTTP 协议的基本格式
a添砖Java
http网络协议网络
HTTP协议("超文本传输协议"),是一个被广泛使用应用层协议,自1991年正式发布HTTP协议以来,HTTP协议就一直在更新,目前已经更新到3.0版本,但是目前主流的依旧是1.1版本,但依旧是一个最主流使用的应用层协议。HTTP协议一般是基于TCP协议实现的,当时知道HTTP3.0开始支持UDP协议实现传输,使用TCP相比较UDP虽然安全,但是速度却相差很多,从3.0版本开始支持UDP协议,为了
- 【计算机网络】传输层数据段格式
菜萝卜子
计算机网络计算机网络网络tcp/ip
在计算机网络中,数据段(Segment)是传输层协议(如TCP或UDP)使用的数据单元。TCP和UDP的数据段格式有所不同,以下是它们的详细说明:1.TCP数据段格式TCP(传输控制协议)是一种面向连接的、可靠的协议,其数据段格式包含多个字段,用于实现可靠传输、流量控制、拥塞控制等功能。TCP数据段的格式如下:字段长度(比特)说明源端口号16发送方的端口号,用于标识发送应用程序。目的端口号16接收
- UDP反射放大攻击.c
金猪报喜-阿尔法
网络安全c语言
#include#include#include#include#include#include#include#include#include#include#defineMAX_PACKET_SIZE8192#definePHI0x9e3779b9#definePACKETS_PER_RESOLVER5staticuint32_tQ[4096],c=362436;structlist{stru
- 网络通信(TCP/UDP协议 三次握手四次挥手 )
羊十一
网络
三、TCP协议与UDP协议1、TCP/IP、TCP、UDP是什么TCP/IP协议是一个协议簇,里面包括很多协议的,UDP只是其中的一个,之所以命名为TCP/IP协议,因为TCP、IP协议是两个很重要的协议,就用他两命名了,而TCP和UDP是位于TCP/IP模型中传输层的两个协议,他们代表着TCP/IP模型所具备的两种通信模式。TCP(TransmissionControlProtocol)传输控制
- TCP/UDP协议特性及TCP三次握手四次挥手详细过程
多谢我很好
tcp/ipudp网络
一、TCP/UDP协议特性1.TCP特性:工作在传输层、面向连接的、可靠的、全双工的、有错误检查的、有半关闭状态的、将数据打包成段、有排序确认机制、有数据恢复重传、流量控制、滑动窗口的传输协议2.UDP特性:工作在传输层、不面向连接的、不可靠的、有限的错误检查、传输性能高、无数据恢复特性的传输协议二、TCP三次握手与四次挥手1.为什么是三次握手和四次挥手三次握手的原因:因为二次握手不能够建立连接而
- 安装数据库首次应用
Array_06
javaoraclesql
可是为什么再一次失败之后就变成直接跳过那个要求
enter full pathname of java.exe的界面
这个java.exe是你的Oracle 11g安装目录中例如:【F:\app\chen\product\11.2.0\dbhome_1\jdk\jre\bin】下的java.exe 。不是你的电脑安装的java jdk下的java.exe!
注意第一次,使用SQL D
- Weblogic Server Console密码修改和遗忘解决方法
bijian1013
Welogic
在工作中一同事将Weblogic的console的密码忘记了,通过网上查询资料解决,实践整理了一下。
一.修改Console密码
打开weblogic控制台,安全领域 --> myrealm -->&n
- IllegalStateException: Cannot forward a response that is already committed
Cwind
javaServlets
对于初学者来说,一个常见的误解是:当调用 forward() 或者 sendRedirect() 时控制流将会自动跳出原函数。标题所示错误通常是基于此误解而引起的。 示例代码:
protected void doPost() {
if (someCondition) {
sendRedirect();
}
forward(); // Thi
- 基于流的装饰设计模式
木zi_鸣
设计模式
当想要对已有类的对象进行功能增强时,可以定义一个类,将已有对象传入,基于已有的功能,并提供加强功能。
自定义的类成为装饰类
模仿BufferedReader,对Reader进行包装,体现装饰设计模式
装饰类通常会通过构造方法接受被装饰的对象,并基于被装饰的对象功能,提供更强的功能。
装饰模式比继承灵活,避免继承臃肿,降低了类与类之间的关系
装饰类因为增强已有对象,具备的功能该
- Linux中的uniq命令
被触发
linux
Linux命令uniq的作用是过滤重复部分显示文件内容,这个命令读取输入文件,并比较相邻的行。在正常情 况下,第二个及以后更多个重复行将被删去,行比较是根据所用字符集的排序序列进行的。该命令加工后的结果写到输出文件中。输入文件和输出文件必须不同。如 果输入文件用“- ”表示,则从标准输入读取。
AD:
uniq [选项] 文件
说明:这个命令读取输入文件,并比较相邻的行。在正常情况下,第二个
- 正则表达式Pattern
肆无忌惮_
Pattern
正则表达式是符合一定规则的表达式,用来专门操作字符串,对字符创进行匹配,切割,替换,获取。
例如,我们需要对QQ号码格式进行检验
规则是长度6~12位 不能0开头 只能是数字,我们可以一位一位进行比较,利用parseLong进行判断,或者是用正则表达式来匹配[1-9][0-9]{4,14} 或者 [1-9]\d{4,14}
&nbs
- Oracle高级查询之OVER (PARTITION BY ..)
知了ing
oraclesql
一、rank()/dense_rank() over(partition by ...order by ...)
现在客户有这样一个需求,查询每个部门工资最高的雇员的信息,相信有一定oracle应用知识的同学都能写出下面的SQL语句:
select e.ename, e.job, e.sal, e.deptno
from scott.emp e,
(se
- Python调试
矮蛋蛋
pythonpdb
原文地址:
http://blog.csdn.net/xuyuefei1988/article/details/19399137
1、下面网上收罗的资料初学者应该够用了,但对比IBM的Python 代码调试技巧:
IBM:包括 pdb 模块、利用 PyDev 和 Eclipse 集成进行调试、PyCharm 以及 Debug 日志进行调试:
http://www.ibm.com/d
- webservice传递自定义对象时函数为空,以及boolean不对应的问题
alleni123
webservice
今天在客户端调用方法
NodeStatus status=iservice.getNodeStatus().
结果NodeStatus的属性都是null。
进行debug之后,发现服务器端返回的确实是有值的对象。
后来发现原来是因为在客户端,NodeStatus的setter全部被我删除了。
本来是因为逻辑上不需要在客户端使用setter, 结果改了之后竟然不能获取带属性值的
- java如何干掉指针,又如何巧妙的通过引用来操作指针————>说的就是java指针
百合不是茶
C语言的强大在于可以直接操作指针的地址,通过改变指针的地址指向来达到更改地址的目的,又是由于c语言的指针过于强大,初学者很难掌握, java的出现解决了c,c++中指针的问题 java将指针封装在底层,开发人员是不能够去操作指针的地址,但是可以通过引用来间接的操作:
定义一个指针p来指向a的地址(&是地址符号):
- Eclipse打不开,提示“An error has occurred.See the log file ***/.log”
bijian1013
eclipse
打开eclipse工作目录的\.metadata\.log文件,发现如下错误:
!ENTRY org.eclipse.osgi 4 0 2012-09-10 09:28:57.139
!MESSAGE Application error
!STACK 1
java.lang.NoClassDefFoundError: org/eclipse/core/resources/IContai
- spring aop实例annotation方法实现
bijian1013
javaspringAOPannotation
在spring aop实例中我们通过配置xml文件来实现AOP,这里学习使用annotation来实现,使用annotation其实就是指明具体的aspect,pointcut和advice。1.申明一个切面(用一个类来实现)在这个切面里,包括了advice和pointcut
AdviceMethods.jav
- [Velocity一]Velocity语法基础入门
bit1129
velocity
用户和开发人员参考文档
http://velocity.apache.org/engine/releases/velocity-1.7/developer-guide.html
注释
1.行级注释##
2.多行注释#* *#
变量定义
使用$开头的字符串是变量定义,例如$var1, $var2,
赋值
使用#set为变量赋值,例
- 【Kafka十一】关于Kafka的副本管理
bit1129
kafka
1. 关于request.required.acks
request.required.acks控制者Producer写请求的什么时候可以确认写成功,默认是0,
0表示即不进行确认即返回。
1表示Leader写成功即返回,此时还没有进行写数据同步到其它Follower Partition中
-1表示根据指定的最少Partition确认后才返回,这个在
Th
- lua统计nginx内部变量数据
ronin47
lua nginx 统计
server {
listen 80;
server_name photo.domain.com;
location /{set $str $uri;
content_by_lua '
local url = ngx.var.uri
local res = ngx.location.capture(
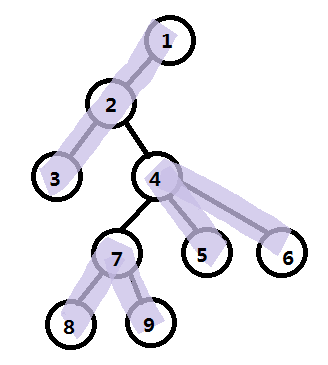
- java-11.二叉树中节点的最大距离
bylijinnan
java
import java.util.ArrayList;
import java.util.List;
public class MaxLenInBinTree {
/*
a. 1
/ \
2 3
/ \ / \
4 5 6 7
max=4 pass "root"
- Netty源码学习-ReadTimeoutHandler
bylijinnan
javanetty
ReadTimeoutHandler的实现思路:
开启一个定时任务,如果在指定时间内没有接收到消息,则抛出ReadTimeoutException
这个异常的捕获,在开发中,交给跟在ReadTimeoutHandler后面的ChannelHandler,例如
private final ChannelHandler timeoutHandler =
new ReadTim
- jquery验证上传文件样式及大小(好用)
cngolon
文件上传jquery验证
<!DOCTYPE html>
<html>
<head>
<meta http-equiv="Content-Type" content="text/html; charset=utf-8" />
<script src="jquery1.8/jquery-1.8.0.
- 浏览器兼容【转】
cuishikuan
css浏览器IE
浏览器兼容问题一:不同浏览器的标签默认的外补丁和内补丁不同
问题症状:随便写几个标签,不加样式控制的情况下,各自的margin 和padding差异较大。
碰到频率:100%
解决方案:CSS里 *{margin:0;padding:0;}
备注:这个是最常见的也是最易解决的一个浏览器兼容性问题,几乎所有的CSS文件开头都会用通配符*来设
- Shell特殊变量:Shell $0, $#, $*, $@, $?, $$和命令行参数
daizj
shell$#$?特殊变量
前面已经讲到,变量名只能包含数字、字母和下划线,因为某些包含其他字符的变量有特殊含义,这样的变量被称为特殊变量。例如,$ 表示当前Shell进程的ID,即pid,看下面的代码:
$echo $$
运行结果
29949
特殊变量列表 变量 含义 $0 当前脚本的文件名 $n 传递给脚本或函数的参数。n 是一个数字,表示第几个参数。例如,第一个
- 程序设计KISS 原则-------KEEP IT SIMPLE, STUPID!
dcj3sjt126com
unix
翻到一本书,讲到编程一般原则是kiss:Keep It Simple, Stupid.对这个原则深有体会,其实不仅编程如此,而且系统架构也是如此。
KEEP IT SIMPLE, STUPID! 编写只做一件事情,并且要做好的程序;编写可以在一起工作的程序,编写处理文本流的程序,因为这是通用的接口。这就是UNIX哲学.所有的哲学真 正的浓缩为一个铁一样的定律,高明的工程师的神圣的“KISS 原
- android Activity间List传值
dcj3sjt126com
Activity
第一个Activity:
import java.util.ArrayList;import java.util.HashMap;import java.util.List;import java.util.Map;import android.app.Activity;import android.content.Intent;import android.os.Bundle;import a
- tomcat 设置java虚拟机内存
eksliang
tomcat 内存设置
转载请出自出处:http://eksliang.iteye.com/blog/2117772
http://eksliang.iteye.com/
常见的内存溢出有以下两种:
java.lang.OutOfMemoryError: PermGen space
java.lang.OutOfMemoryError: Java heap space
------------
- Android 数据库事务处理
gqdy365
android
使用SQLiteDatabase的beginTransaction()方法可以开启一个事务,程序执行到endTransaction() 方法时会检查事务的标志是否为成功,如果程序执行到endTransaction()之前调用了setTransactionSuccessful() 方法设置事务的标志为成功则提交事务,如果没有调用setTransactionSuccessful() 方法则回滚事务。事
- Java 打开浏览器
hw1287789687
打开网址open浏览器open browser打开url打开浏览器
使用java 语言如何打开浏览器呢?
我们先研究下在cmd窗口中,如何打开网址
使用IE 打开
D:\software\bin>cmd /c start iexplore http://hw1287789687.iteye.com/blog/2153709
使用火狐打开
D:\software\bin>cmd /c start firefox http://hw1287789
- ReplaceGoogleCDN:将 Google CDN 替换为国内的 Chrome 插件
justjavac
chromeGooglegoogle apichrome插件
Chrome Web Store 安装地址: https://chrome.google.com/webstore/detail/replace-google-cdn/kpampjmfiopfpkkepbllemkibefkiice
由于众所周知的原因,只需替换一个域名就可以继续使用Google提供的前端公共库了。 同样,通过script标记引用这些资源,让网站访问速度瞬间提速吧
- 进程VS.线程
m635674608
线程
资料来源:
http://www.liaoxuefeng.com/wiki/001374738125095c955c1e6d8bb493182103fac9270762a000/001397567993007df355a3394da48f0bf14960f0c78753f000 1、Apache最早就是采用多进程模式 2、IIS服务器默认采用多线程模式 3、多进程优缺点 优点:
多进程模式最大
- Linux下安装MemCached
字符串
memcached
前提准备:1. MemCached目前最新版本为:1.4.22,可以从官网下载到。2. MemCached依赖libevent,因此在安装MemCached之前需要先安装libevent。2.1 运行下面命令,查看系统是否已安装libevent。[root@SecurityCheck ~]# rpm -qa|grep libevent libevent-headers-1.4.13-4.el6.n
- java设计模式之--jdk动态代理(实现aop编程)
Supanccy2013
javaDAO设计模式AOP
与静态代理类对照的是动态代理类,动态代理类的字节码在程序运行时由Java反射机制动态生成,无需程序员手工编写它的源代码。动态代理类不仅简化了编程工作,而且提高了软件系统的可扩展性,因为Java 反射机制可以生成任意类型的动态代理类。java.lang.reflect 包中的Proxy类和InvocationHandler 接口提供了生成动态代理类的能力。
&
- Spring 4.2新特性-对java8默认方法(default method)定义Bean的支持
wiselyman
spring 4
2.1 默认方法(default method)
java8引入了一个default medthod;
用来扩展已有的接口,在对已有接口的使用不产生任何影响的情况下,添加扩展
使用default关键字
Spring 4.2支持加载在默认方法里声明的bean
2.2
将要被声明成bean的类
public class DemoService {