纪中暑假集训 2020.07.17【NOIP提高组】模拟 反思+题解

昨天刚辉煌一天，今天就……题目个人认为难度还是可以的，82分 （打得烂得一批） ，第19，还是要多加练习！

T1：【NOIP2017模拟8.14A组】亲戚

Description

Input

Output

Sample Input

4
0 1 1 0

Sample Output

8

Data Constraint

反思&题解

比赛思路： 懵，只能暴力
正解思路： 这道题有两种方法：
1. 据各位大佬说很明显是树形DP……（为啥我看不出来）
首先要我们建一个编号为0的根，$f[i]$处理完第i个节点以及他的子孙时的方案数，很显然最后输出$f[0]$
设$size[i]$为以$i$为根的子树的节点个数，x是当前遍历到的点，v是它的儿子
这里先给出转移方程：
$f[x]=((f[x]\ast f[v])\ast C(min(size[x]-1,size[v]),size[x]-1+size[v]))$
首先，$f[x]\ast f[v]$是根据乘法原理先匹配，之后用组合数公式求出放儿子子树节点的个数的方案数
而下一个难搞的地方就是组合数取模，首先，众所周知组合数的公式为：

$C_m^n=\frac{m!}{n!(n-m)!}$

我们一开始可以把阶乘预处理好，之后由于要模1000000007，所以我们就需要用到逆元，求逆元有非常多的方法，但是由于我只会费马小定理认为费马小定理比较简单，所以就用这个
首先我们知道费马小定理：（在p为质数且与a互质得情况下）

$a^{p-1}\equiv 1$ $($$mod$ $p$$)$

从这可以推出：

$a/b=a\ast b^{p-2}$ $(mod$ $p)$

如果想深入理解的话，可以参考这篇博客
2. 一种很奇妙的方法：首先还是要弄一个编号为0的根
如果不考虑任何规矩，那么n个点的排序个数就是$n!$
之后我们去看每一个子树，设子树x有m个节点，我们假设除了根节点以外其他$m-1$个节点都放好了位置，那么根节点就有m个位置可以放，
但是因为题目的要求，只有放在1个位置是也就是第1个位置合法的，其他$m-1$个位置都是不合法的，
所以对于每个子树来说合法的个数就是 $\frac{1}{m}$，
然后由乘法原理得，全部子树总共的合法方案就是$\frac{1}{m_1}\ast$$\frac{1}{m_2}\ast \dots \ast$$\frac{1}{m_n}$
最后再用$n!$乘/除一下就行了
之后还是要用逆元……（别想了，逃不掉的，主要是出题人想搞事情）
反思： 还是对于树的知识点要加强……

CODE

方法1：

#include
using namespace std;
struct node{
	int to,next;
}edge[400005];
const int mo=1000000007;
int head[400005],cnt,size[400005],n;
long long f[400005],jc[400005];
void add(int u,int v)
{
	edge[++cnt].to=v;
	edge[cnt].next=head[u];
	head[u]=cnt;
}
long long power(long long x,long long y)
{
	long long tot=1;
	while (y)
	{
		if (y&1) tot=(x*tot)%mo;
		y>>=1;
		x=(x*x)%mo;
	}
	return tot;
}
long long C(long long n,long long m)
{
	return jc[m]*power(jc[m-n]*jc[n]%mo,mo-2)%mo;
}
void dfs(int fa,int x)
{
	size[x]=1;
	f[x]=1;
	int i;
	for (i=head[x];i;i=edge[i].next)
	{
		int v=edge[i].to;
		if(v==fa) continue;
		dfs(x,v);
		f[x]=((f[x]*f[v])%mo*C(min(size[x]-1,size[v]),size[x]-1+size[v]))%mo;
		size[x]+=size[v];
	}
}
int main()
{
	jc[0]=1;
	int i;
	for(i=1;i<200005;i++)
		jc[i]=(jc[i-1]*i)%mo;
	scanf("%d",&n);
	int father;
	for(i=1;i<=n;i++)
	{
		scanf("%d",&father);
		add(father,i);
		add(i,father);
	}
	dfs(0,0);
	printf("%lld",f[0]);
}

方法2：

#include
using namespace std;
struct arr
{
	int to,next;
}edge[200005];
int n,head[200005],son[200005],cnt,f[200005],m;
long long ans;
const int mo=1000000007;
void add(int u,int v)
{
	edge[++cnt].to=v;
	edge[cnt].next=head[u];
	head[u]=cnt;
}
long long power(long long x,long long y)
{
	long long tot=1;
	while (y)
	{
		if (y&1) tot=(x*tot)%mo;
		y>>=1;
		x=(x*x)%mo;
	}
	return tot;
}
void dg(int now)
{
	f[now]=1;
	if (son[now])
	{
		int i;
		for (i=head[now];i;i=edge[i].next)
		{
			int v=edge[i].to;
			dg(v);
			f[now]+=f[v];
		}
	}
}
int main()
{
	scanf("%d",&n);
	int i,fa;
	ans=1;
	for (i=1;i<=n;i++)
	{
		scanf("%d",&fa);
		son[fa]++;
		add(fa,i);
	}
	for (i=1;i<=n;i++)
		ans=ans*i%mo;
	dg(0);
	for (i=1;i<=n;i++)
		ans=ans*power(f[i],mo-2)%mo;
	printf("%d\n",ans);
	return 0;
}

T2：【NOIP2017模拟8.14A组】数组

Description

Input

Output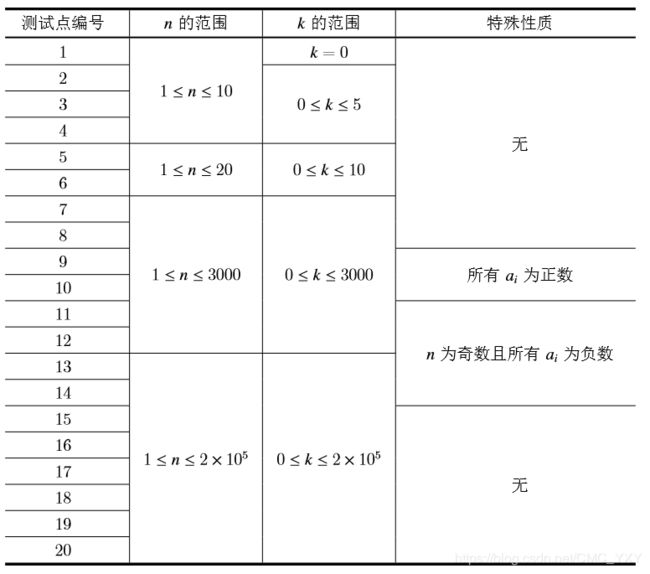Sample Input

输入样例1：
3 2 7
5 4 2

输入样例2：
5 3 1
5 4 3 5 5

Sample Output

输出样例1：
999999732

输出样例2：
0

Data Constraint

反思&题解

比赛思路： 懵，样例没看懂
正解思路： 首先解释一下怎么取模，对于负数来说，就是结果加上要模得数之后再取模
题目分两种情况讨论：
1. 如果输入进来的数组乘起来为负数：先打个标记，因为相对于负数来说绝对值越大这个负数就越小，之后把他们全部变成正数，之后用小根堆一直找最小的把他加上x就行了
2. 如果输入进来的数组乘起来为正数，那么先想办法把最小的数变成负数，如果不行，就把k次减得机会都给这个最小的数；反之可以的话就将剩下得次数想地1中情况那样做就行了
反思： 读题能力要加强，看懂了样例这题估计就对了

CODE

#include
using namespace std;
const long long mo=1000000007;
long long x,heap[200005],a[200005],ans;
int n,k,bz;
void up(int now)
{
	while (now>1 && heap[now]<heap[now>>1])
	{
		swap(heap[now],heap[now>>1]);
		now>>=1;	
	}	
}
void down(int now)
{
	while (now*2<=n && heap[now*2]<heap[now] || now*2+1<=n && heap[now*2+1]<heap[now])
	{
		if (now*2+1<=n && heap[now*2+1]<heap[now*2])
		{
			swap(heap[now],heap[now*2+1]);
			now=now*2+1;
		}
		else
		{
			swap(heap[now],heap[now*2]);
			now<<=1;
		}
	}
}//老实人手打堆
int main()
{
	scanf("%d%d%lld",&n,&k,&x);
	int num,i;
	long long mn=1234567890;
	bz=1;
	for (i=1;i<=n;i++)
	{
		scanf("%lld",&a[i]);
		if (a[i]<0)
		{
			a[i]=-a[i];
			bz=-bz;
		}
		if (a[i]<mn)
		{
			mn=a[i];
			num=i;
		}
	}
	if (bz==-1)
	{
		for (i=1;i<=n;i++)
		{
			heap[i]=a[i];
			int t=i;
			up(t);
		}
		while (k--)
		{
			heap[1]+=x;
			down(1);
		}
		ans=bz;
		for (i=1;i<=n;i++)
			ans=(ans*heap[i])%mo;
		ans=(ans+mo)%mo;
		printf("%lld\n",ans);
	}
	else
	{
		ans=bz;
		int tot=0;
		for (i=1;i<=k;i++)
		{
			if (x*i>a[num])
			{
				tot=i;
				break;	
			}	
		}
		if (!tot)
		{
			a[num]-=k*x;
			for (i=1;i<=n;i++)
				ans=ans*a[i]%mo;
			printf("%lld\n",ans);	
		}
		else
		{
			a[num]-=tot*x;
			a[num]=-a[num];
			k-=tot;
			for (i=1;i<=n;i++)
			{
				heap[i]=a[i];
				int t=i;
				up(t);
			}
			while (k--)
			{
				heap[1]+=x;
				down(1);
			}
			ans=-1;
			for (i=1;i<=n;i++)
				ans=(ans*heap[i])%mo;
			ans=(ans+mo)%mo;
			printf("%lld\n",ans);	
		}	
	}
	return 0;
}

T3：【NOIP2017模拟8.14A组】水管

Description

Input

Output

Sample Input

1
5 7
1 2 2
1 4 1
2 4 2
4 3 2
2 3 1
4 5 1
1 5 2

Sample Output

5
No

Data Constraint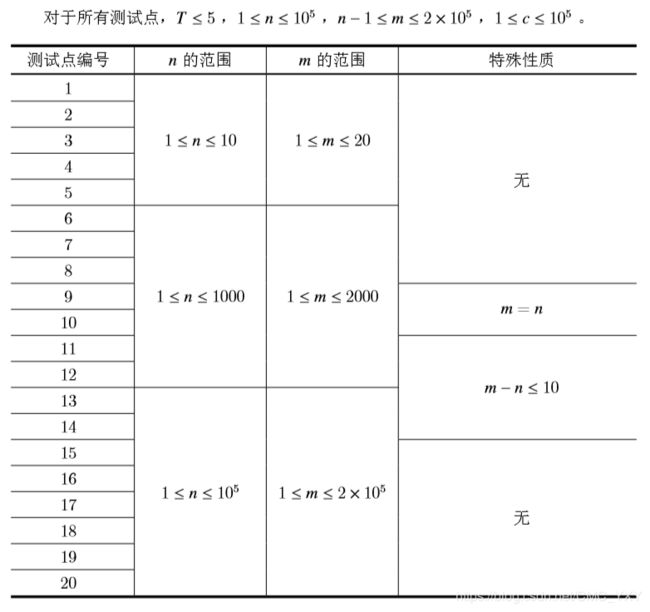

Hint

反思&题解

比赛思路： 先排一次序做最小生成树，在把相同权值得边得顺序换一下，再做一遍最小生成树，看看了两个生成树是不是一样的（不过听说这个方法是可以过的，估计是我哪个细节打错了）这种方法的题解
正解思路： 在处理一条边的时候把权值相同的边判断一下就行了
反思： 程序实现能力有待加强，不然可以A掉的

CODE

#include
using namespace std;
struct arr
{
	int u,v,w;
}a[400005];
int n,m,t,father[200005];
long long ans; 
int find(int k)
{
	if (father[k]==k) return k;
	father[k]=find(father[k]);
	return father[k];
}
bool cmp(arr x,arr y)
{
	return x.w<y.w;
}
int main()
{
	scanf("%d",&t);
	while (t--)
	{
		scanf("%d%d",&n,&m);
		int i;
		for (i=0;i<=n;i++)
			father[i]=i;
		for (i=1;i<=m;i++)
			scanf("%d%d%d",&a[i].u,&a[i].v,&a[i].w);
		ans=0;
		sort(a+1,a+1+m,cmp);
		int tot=1;
		bool bz=false;
		for (i=1;i<=m;i++)
		{
			int t1,t2;
			t1=find(a[i].u);
			t2=find(a[i].v);
			if (t1!=t2)
			{
				if (!bz)
				{
					int j;
					for (j=i+1;j<=m;j++)
					{
						if (a[i].w==a[j].w)
						{
							int tt1,tt2;
							tt1=find(a[j].u);
							tt2=find(a[j].v);
							if ((tt1==t1 && tt2==t2) || (tt1==t2 && tt2==t1))
							{
								bz=true;
								break;
							}
						}
						else break;
					}
				}
				father[t1]=t2;
				tot++;
				ans+=a[i].w;
				if (tot==n) break;
			}
		}
		printf("%lld\n",ans);
		if (bz) printf("No\n");
		else printf("Yes\n");
	}
	return 0;
}