NOIP模拟赛2题 解？

前言

花了1个多小时搞T1,因为没有写好判断导致错误，然后又转去做T3，本来想出了两重循环但是脑子秀逗了准备手推打表代码。。。超级悲惨爆零33名滚粗
满分：100+100+100+100=400
得分：0+0+0+0=0

T1

A. 字符串的展开(expand.cpp)
题目描述
在初赛普及组的“阅读程序写结果”的问题中，我们曾给出一个字符串展开的例子：如果在输入的字符串中，含有类似于“d-h”或者“4-8”的字串，我们就把它当作一种简写，输出时，用连续递增的字母或数字串替代其中的减号，即，将上面两个子串分别输出为“defgh”和“45678”。在本题中，我们通过增加一些参数的设置，使字符串的展开更为灵活。具体约定如下：

(1)遇到下面的情况需要做字符串的展开：在输入的字符串中，出现了减号“-”，减号两侧同为小写字母或同为数字，且按照ASCII码的顺序，减号右边的字符严格大于左边的字符。

(2)参数p1：展开方式。p1=1时，对于字母子串，填充小写字母；p1=2时，对于字母子串，填充大写字母。这两种情况下数字子串的填充方式相同。p1=3时，不论是字母子串还是数字字串，都用与要填充的字母个数相同的星号“*”来填充。

(3)参数p2：填充字符的重复个数。p2=k表示同一个字符要连续填充k个。例如，当p2=3时，子串“d-h”应扩展为“deeefffgggh”。减号两边的字符不变。

(4)参数p3：是否改为逆序：p3=1表示维持原来顺序，p3=2表示采用逆序输出，注意这时候仍然不包括减号两端的字符。例如当p1=1、p2=2、p3=2时，子串“d-h”应扩展为“dggffeeh”。

(5)如果减号右边的字符恰好是左边字符的后继，只删除中间的减号，例如：“d-e”应输出为“de”，“3-4”应输出为“34”。如果减号右边的字符按照ASCII码的顺序小于或等于左边字符，输出时，要保留中间的减号，例如：“d-d”应输出为“d-d”，“3-1”应输出为“3-1”。

输入格式
输入文件expand.in包括两行：

第1行为用空格隔开的3个正整数，一次表示参数p1，p2，p3。

第2行为一行字符串，仅由数字、小写字母和减号“-”组成。行首和行末均无空格。

输出格式
输出文件expand.out只有一行，为展开后的字符串。

样例
样例1输入
1 2 1
abcs-w1234-9s-4zz
样例1输出
abcsttuuvvw1234556677889s-4zz
样例2输入
2 3 2
a-d-d
样例2输出
aCCCBBBd-d
样例3输入
3 4 2
di-jkstra2-6
样例3输出
dijkstra2************6
数据范围与提示
40%的数据满足：字符串长度不超过5

100%的数据满足：1<=p1<=3，1<=p2<=8，1<=p3<=2。字符串长度不超过100

很明显这是一道模拟题，并且要注意的细节很多，比如在判断左右两端时可以直接看是否是数字或小写字母，在输出完填充的数字后i+1来删掉’-'号
在判断右边字符是否为左边字符的后继时可以不用在多写判断，因为他们两个之间没有可以输出的字符或数字了（相差仅为1）

#include  
#include  
using namespace std;
char c[50005];
int main() {
	int p1,p2,p3;
	scanf("%d%d%d",&p1,&p2,&p3);
	scanf("%s",c+1);
	int n=strlen(c+1);
	for(int i = 1; i <= n; i++) {
		printf("%c",c[i]);
		if(c[i + 1]=='-'&&c[i]<c[i+2]&&(('0'<= c[i]&&c[i]<='9'&&'0'<=c[i+2]&&c[i+2]<='9')||('a' <=c[i]&&c[i]<='z'&&'a'<=c[i+2]&&c[i+2]<='z'))) { 
			if('0'<=c[i]&&c[i]<='9'&&'0'<=c[i+2]&&c[i+2]<='9') {//如果是数字
				if(p1 == 3) {  
					for(int j=c[i]+1;j<=c[i+2]-1;j++) 
					{
						for(int k=1;k<=p2;k++)
						{
							printf("*");
						}
					}				
				}
				else {
					if(p3==1) { //正序
						for(int j=c[i]+1;j<=c[i+2]-1;j++) 
						{
							for(int k=1;k<=p2;k++) 
							{
								printf("%c",j);
							}
						}	
					}
					else { //如果是逆序
						for(int j=c[i+2]-1;j>=c[i]+1;j--) 
						{
							for(int k=1;k<=p2;k++)
							{
								printf("%c",j);
							}
						}								
					}					
				}
			}
			else {//不是数字，那么两边就是字母
				if(p1==3) { 
					for(int j=c[i]+1;j<=c[i+2]-1;j++) 
					{   
					    for(int k = 1; k <= p2; k++)
						{
							printf("*");
						}
					} 		
				}
				else if(p1==1) { //输出小写字母
					if(p3==1) { //正序
						for(int j=c[i]+1;j<=c[i+2]-1;j++) 
						{
							for(int k=1;k<=p2;k++)
							{
							printf("%c",j);
							}
						}
					}
					else { //逆序
						for(int j=c[i+2]-1;j>=c[i]+1;j--) 
						{
							for(int k=1;k<=p2;k++)
							{
								printf("%c",j);	
							}
						}								
					}					
				}	
				else { //输出大写字母
					if(p3==1) { //正序
						for(int j=c[i]+1;j<=c[i+2]-1;j++) 
						{
							for(int k=1;k<=p2;k++)
							{
								printf("%c",j+ 'A'-'a');
							}	
						}
					}
					else { //逆序
						for(int j=c[i+2]-1;j>=c[i]+1;j--) 
						{
							for(int k=1;k<=p2;k++)
							{
								printf("%c",j+'A'-'a');	
							}
						}				
					}						
				}			
			} 
			i+=1;//删掉'-'号
		}
	}
	return 0;
}

T2

B. 作业调度方案（jsp.cpp）
题目描述
我们现在要利用m台机器加工n个工件，每个工件都有m道工序，每道工序都在不同的指定的机器上完成。每个工件的每道工序都有指定的加工时间。

每个工件的每个工序称为一个操作，我们用记号j-k表示一个操作，其中j为1到n中的某个数字，为工件号；k为1到m中的某个数字，为工序号，例如2-4表示第2个工件第4道工序的这个操作。在本题中，我们还给定对于各操作的一个安排顺序。

例如，当n=3，m=2时，“1-1，1-2，2-1，3-1，3-2，2-2”就是一个给定的安排顺序，即先安排第1个工件的第1个工序，再安排第1个工件的第2个工序，然后再安排第2个工件的第1个工序，等等。

一方面，每个操作的安排都要满足以下的两个约束条件。

(1)对同一个工件，每道工序必须在它前面的工序完成后才能开始；

(2)同一时刻每一台机器至多只能加工一个工件。

另一方面，在安排后面的操作时，不能改动前面已安排的操作的工作状态。 由于同一工件都是按工序的顺序安排的，因此，只按原顺序给出工件号，仍可得到同样的安排顺序，于是，在输入数据中，我们将这个安排顺序简写为“1 1 2 3 3 2”。

还要注意，“安排顺序”只要求按照给定的顺序安排每个操作。不一定是各机器上的实际操作顺序。在具体实施时，有可能排在后面的某个操作比前面的某个操作先完成。

例如，取n=3,m=2，已知数据如下：

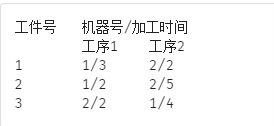
工件号 机器号/加工时间
工序1 工序2
1 1/3 2/2
2 1/2 2/5
3 2/2 1/4
则对于安排顺序“1 1 2 3 3 2”，下图中的两个实施方案都是正确的。但所需要的总时间分别是10与12。

当一个操作插入到某台机器的某个空档时（机器上最后的尚未安排操作的部分也可以看作一个空档），可以靠前插入，也可以靠后或居中插入。为了使问题简单一些，我们约定：在保证约束条件（1）（2）的条件下，尽量靠前插入。并且，我们还约定，如果有多个空档可以插入，就在保证约束条件（1）（2）的条件下，插入到最前面的一个空档。于是，在这些约定下，上例中的方案一是正确的，而方案二是不正确的。

显然，在这些约定下，对于给定的安排顺序，符合该安排顺序的实施方案是唯一的，请你计算出该方案完成全部任务所需的总时间。

输入格式
输入文件jsp.in的第1行为两个正整数，用一个空格隔开：

m n

（其中m（<20）表示机器数，n（<20）表示工件数）

第2行：m*n个用空格隔开的数，为给定的安排顺序。

接下来的2n行，每行都是用空格隔开的m个正整数，每个数不超过20。

其中前n行依次表示每个工件的每个工序所使用的机器号，第1个数为第1个工序的机器号，第2个数为第2个工序机器号，等等。

后n行依次表示每个工件的每个工序的加工时间。

可以保证，以上各数据都是正确的，不必检验。

输出格式
输出文件jsp.out只有一个正整数，为最少的加工时间。

样例
样例输入
2 3
1 1 2 3 3 2
1 2
1 2
2 1
3 2
2 5
2 4
样例输出
10

这也是道模拟题（而且是大模拟。。。）我们可以用一个数组来记录每个工序完成的最后时间（总时间就是最后完成的时间）使用一个变量s来记录目前工作最多能够占用的时间。同时使用一个flag数组来判断某个时间段是否此工序需要的机器被占用，如果没有，那么就将s++，否则只要有一个时间点无法使用，s就清零重来，如果s==此工作在第j道工序时要用的时间，把这段时间标记为已用过，（此工作的）最后时间更新为j，继续找下一个按顺序安排的工作

#include
#include
using namespace std;
int work[21];//工序的安排情况
int num[441];//工序安排的顺序
int lastshijian[21];//第i件工作的最后时间
int need[21][21];//第i件工作加工第j个工序需要的机器
int shijian[21][21];//第i件物品加工第j个工序需要的时间
bool flag[21][441];//判断占用情况
int m,n,ans=0,s=0;
int main()
{
	scanf("%d%d",&m,&n);
	for(int i=1;i<=n*m;i++)
	{
		scanf("%d",&num[i]);
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			scanf("%d",&need[i][j]);
		}
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			scanf("%d",&shijian[i][j]);
		}
	}
	//开始膜你
	for(int i=1;i<=n*m;i++)
	{
		work[num[i]]++;
		for(int j=lastshijian[num[i]]+1;;j++){//从空闲时间开始枚举
			if(flag[need[num[i]][work[num[i]]]][j]==0)//如果没有被占用
			{
				s++;//时间++
			}
			else{
				s=0;//只要有一个时间点已被占用就不行
			}
			if(s==shijian[num[i]][work[num[i]]])//可以安排第i件工序
			{
				for(int k=j-s+1;k<=j;k++)//时间段标记为已使用
				{
					flag[need[num[i]][work[num[i]]]][k]=1;
				}
			lastshijian[num[i]]=j;//更新最后时间
			s=0;
			break;
			}
		}
	}
	for(int i=1;i<=n;i++)//找出最大用时
	{
		ans=max(ans,lastshijian[i]);
	}
	printf("%d\n",ans);
	return 0;
}

T3

C. 火柴棒等式（matches.cpp）

题目描述
给你n根火柴棍，你可以拼出多少个形如“A+B=C”的等式？等式中的A、B、C是用火柴棍拼出的整数（若该数非零，则最高位不能是0）。用火柴棍拼数字0-9的拼法如图所示：

注意：

1.加号与等号各自需要两根火柴棍

2.如果A≠B，则A+B=C与B+A=C视为不同的等式（A、B、C>=0）

3.n根火柴棍必须全部用上

输入格式
输入文件matches.in共一行，又一个整数n（n<=24）。

输出格式
输出文件matches.out共一行，表示能拼成的不同等式的数目。

样例
样例1输入
14
样例1输出
2
样例2输入
18
样例2输出
9
数据范围与提示
【输入输出样例1解释】

2个等式为0+1=1和1+0=1。

【输入输出样例2解释】

9个等式为：

0+4=4

0+11=11

1+10=11

2+2=4

2+7=9

4+0=4

7+2=9

10+1=11

11+0=11

这也是道模拟，因为数据较小，思路是记录每个数字需要用到的火柴根数,然后用两重循环暴力枚举答案可能的种数即可
考试时因为执着于手推所以放弃了这个思路。。。

#include
#include
using namespace std;
int n,ans=0,a[10]={6,2,5,5,4,5,6,3,7,6};
int zhi(int x)
{
	int z=0;
	if(x>=0&&x<=9)
	{
		return a[x];
	}
	while(x)//枚举更多位数的火柴根数
	{
		z+=a[x%10];
		x/=10;
	}
	return z;
}
int main()
{
	scanf("%d",&n);
	n-=4;//加号和等号要用去四根
	for(int i=0;i<=1000;i++)
	{
		for(int j=0;j<=1000;j++)
		{
			int t=i+j;
			if(zhi(i)+zhi(j)+zhi(t)==n){//如果一共花费的火柴根数==n
				ans++;
			}
		}
	}
	printf("%d",ans);
	return 0;
}

T4

过菜还不会。。。

总结

这是我这个暑假爆的第二次零了。。感觉和第一次一样，都是因为有思路却不知如何实现，同时我觉得自己应该要调整好考试时的心态，专心做题，而不是将脑袋用来担心自己的成绩
要继续加油啊！