剪绳子问题解法及对于贪心和递归算法的理解
剪绳子问题是剑指offer算法题中一道考察贪心和动态规划算法的题,在做这道题的时候有两种基本的做法:将绳子尽可能分成长度为3和2,并且优先3,另一种解法是动态规划解法;当时自己对于贪心和DP并不能区分的特别清楚,并且做完这道题还不能够完全理解,因此又借助网上资料才能窥得一二,记录如下。
题目:给你一根长度为n的绳子,请把绳子剪成整数长的m段(m、n都是整数,n>1并且m>1),每段绳子的长度记为k[0],k[1],...,k[m]。请问k[0]xk[1]x...xk[m]可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
- 解法一:贪心算法
简单来说,就是将一段绳子分为m段,使得m段长度乘起来积最大,最直观的想法是子段肯定不是越长越好,假如不分,积就是他本身的长度(当然题干要求最少要分两段),那么就往小了分,但是1肯定不行,这样的话积就是1了,因此我们慢慢往上看:
对于2和3: 是先分2好,还是先分3好? 3*(n-3) > 2*(n-2) 求解出来是 n>5,也就是说n>5的时候分3比分2好
对于4:4的话先分3,那就是1*3=3,还不如不分,分2为2*2=4,所以4不分或者是分2一样,为了统一,我们遇到4就分成2+2
对于5:最好的方法是分段,因为3*2>5
对于6:当然也是分段要好
...
我们可以看到从5开始,分段就比不分段要好了,可以这样想一下,当绳子长度为100时,我想先切一段,那第一刀切多少呢?只要是第一刀切4以上就不合理,因为我总能把4以上的数分成2和3组合,且比原段要长,所以只能分3或者2,那么分哪个呢?我们根据 3*(n-3) > 2*(n-2) 求解出来是 n>5,知道当n>5的时候优先分3,再分2(分1就不用考虑了,肯定不划算)
因此我们有了以下策略:当 n>=5 的时候,优先分3再分2,这时候我们就有了以下3种情况:
n%3 == 0: 全分3,不分2
n%3 == 1: 最后一个3和余下的1分成两个2
n%3 == 2: 全分3,最后余数分2
因此程序如下:
class Solution {
public:
int cutRope(int n) {
if(n == 2)return 1;
if(n == 3)return 2;
if(n<2 || n>60)return -1;
int x = n/3;
int y = n%3;
if(y == 0) return pow(3, x);
else if(y == 1)return pow(3, x-1)*4;
else return pow(3, x)*2;
}
};其实这种程序的写法是因为我们知道了每次分3是最优的,所以直接算出了需要分多少个3,但是并不符合贪心的思想,贪心的想法是:我不知道总体分成什么样的最好,我只知道当n>=5的时候,我当前最好的方法就是分3,至于分完之后的事不是我该考虑的,因此按照这个想法我们有如下程序:
public int cutRope(int target) {
int max=1;
if(target<=3 && target>0){
return target-1;
}
while(target>4){
target-=3;
max*=3;
}
return max*target;
}
至于有没有对于先分3再分2有没有严格的数学证明,我在牛客网上看到一种数学证明:
链接:https://www.nowcoder.com/questionTerminal/57d85990ba5b440ab888fc72b0751bf8?f=discussion
来源:牛客网
问题类似于定周长求最大面积的问题(例如给定四边形周长,求最大面积),当k[0]==k[1]==,==k[m]时乘积最大,设k[0]=x,那么n=x*m,乘积可以用下式表示
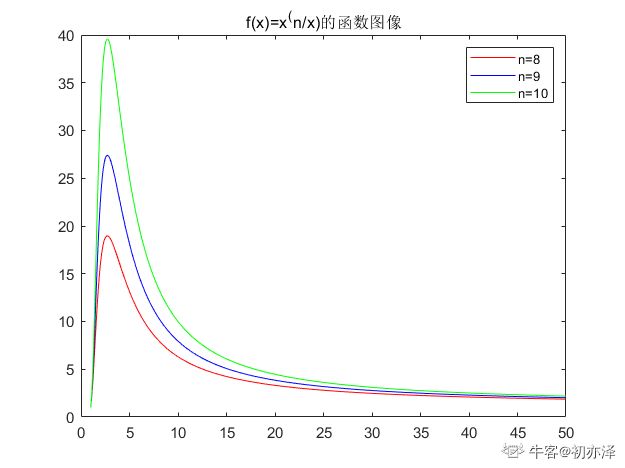
f(x)=(x)^(n/x)
下面是f(x)的导数:
乘积函数在n/m=e的时候,取得最大值,可知,当x∈(0,e)时f(x)单调递增,当x>e时,单调递减,因此,在x=e时取得最大值,e≈2.718,是自然对数。
从函数图像上也可以看出这一点f(x)的函数图像
又因为x的取值只能为整数,且f(3)>f(2),所以,当n>3时,将n尽可能地分割为3的和时,乘积最大。
- 解法二:DP算法
对于 n>=5 的绳子,必然存在分段点,那么我们假设dp[n]是长度为n的绳子积的最大值,那么我一定能够找到一个点,将长度为n的绳子分为长度为 i 和 n-i 的两段,使得dp[i]与dp[n-i]的乘积为长度为n的绳子的最大值,即 dp[n] = dp[i] * dp[n-i], 代码如下:
class Solution {
public:
int cutRope(int n) {
if(n < 4)return n-1;
int* dp = new int[n+1];
dp[0] = 0; //此处的赋值和真实的解不一样,因为剩余2和3时可以不分
dp[1] = 1;
dp[2] = 2;
dp[3] = 3;
for (int i = 4; i其实写到这里上面的剪绳子的题就解完了,但是为了对贪心算法和动态规划有更好的认识,又找了一个最小路径的题,这个可以帮助我们更好的理解这两者的不同。
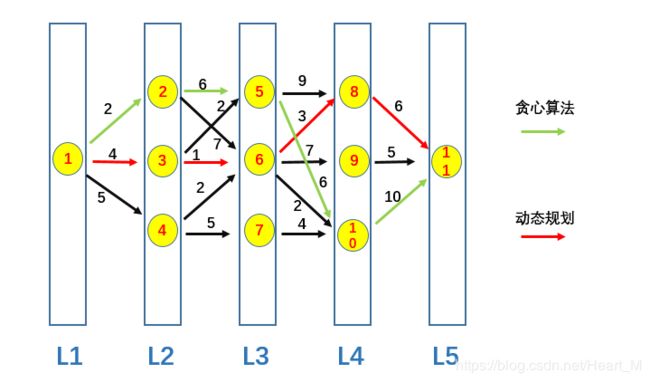
如上图所示,求从车站1到车站11的最短路径,L1~L5为5个城市
按照贪心算法,其只专注于当前问题的最优解,从L1-L2,选择最短路径1-2,然后从2至L3选择最短路径2-6,...,因此贪心算法最后给出的路径为绿色线条,每一步都是再当时情况下的最短路径,但是集合起来却不是最短的。贪心算法不一定会得到最后的最优解,但是一旦证明这种方法最优,那么贪心算法效率快的特点就能发挥出来,比如说最小生成树的Prim和Kruskal就是漂亮的贪心算法。
按照动态规划,其会保存所有的最佳路径,比如到达L3的时候,从1至5,6,7三个车站的最优路径都被记录,然后前往L4的时候,就会根据所记录的路径更新到达8,9,10三个车站的最短路径,因此最终的结果一定是最优的,DP算法的本质其实是遍历了所有的情况,只不过是保存了之前的结果,不用重复计算了。
- 简单总结一下:
贪心算法:只关注子问题的最优,不考虑全局,不一定能得到全局最优的结果,但是一旦被证明可行,其效率很高
动态规划:本质上遍历了所有可能性,一定能达到全局最优,但是效率不如贪心算法高