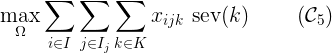作者|Antoine Champion
编译|VK
来源|Towards Data Science
机器学习和深度学习一直是业界的热门话题。品牌领先于功能,导致深度学习在许多人工智能应用中被过度使用。
这篇文章将提供对约束求解的快速理解,这是一个强大但未被充分利用的方法,可以解决人工智能和其他计算机科学领域的大量问题,例如物流和调度时间推理和图形问题。
解决现实问题
让我们来考虑一个事实性的和高度话题性的问题。
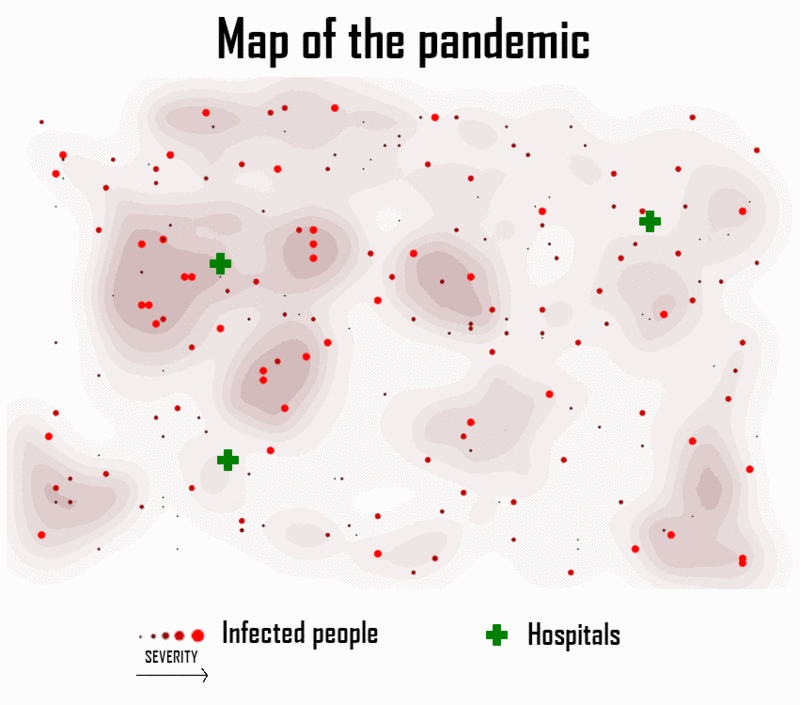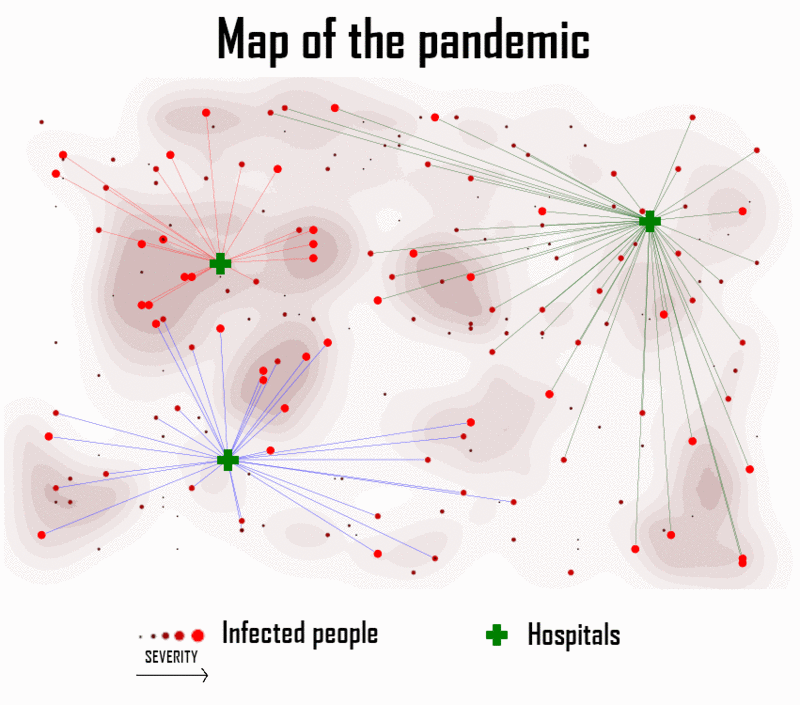
病人人数正在上升。医院必须迅速组织起来治疗病人。
世界上需要一种算法,在疾病严重程度、患者年龄和位置、医院容量和设备等多个标准下,将感染者和医院匹配起来。
许多人会说,神经网络将是最适合它的:它可以有不同的配置,广泛的参数范围,可以根据需要减少到一个独特的解决方案。
然而,也有一些不利因素会破坏这个方案:
- 模型需要训练,因此需要以前案例的历史数据,
- 清理和整合数据集会浪费很多时间,
- 各种体系结构都需要通过冗长的训练并且要进行测试。
另一方面,如果用一个布尔可满足性问题来描述,在不确定多项式时间(NP完全问题)中仍然给出次优解,并且不需要任何历史数据的情况下,不会有上述任何缺点。
这篇文章帮助你快速一览CSPs。理论和问题的表述将被忽略。有关更严格的方法,请参考论文,论文在文章的末尾
抽象问题
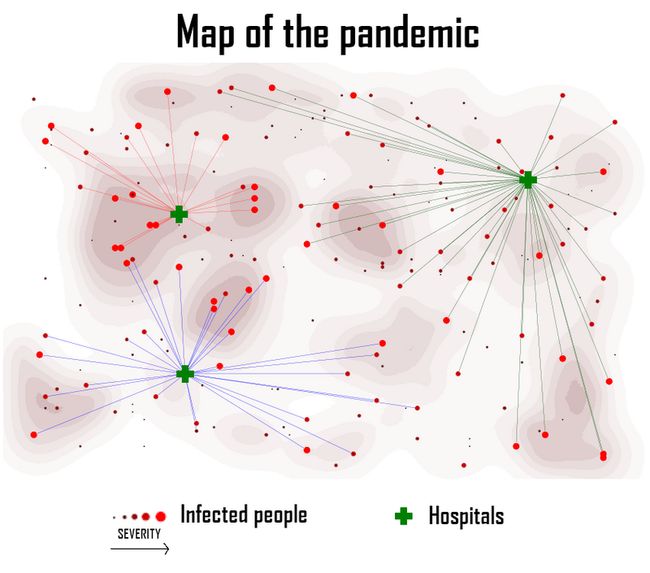
这篇文章将介绍约束编程,旨在解决这个案例。上面那张图说明了我们算法的输出,应该该算法将感染者与医院匹配。现有几个框架用于约束求解。Google Optimization Tools(又称Tools)是一个用于解决组合优化问题的开源软件套件。我们的问题将使用Python中的这个框架进行建模。
from ortools.sat.python import cp_modelcolab:https://colab.research.google...
参数
现在,让我们将问题简化为4个参数(1):
- 感染者所在地
- 感染者的严重程度
- 医院位置
- 每家医院的床位数
让我们用python定义这些参数:
# 医院数量
n_hospitals = 3
# 感染者人数
n_patients = 200
# 每家医院的床位数
n_beds_in_hospitals = [30,50,20]
# 病人位置,tuple (x,y)
patients_loc = [(randint(0, 100), randint(0, 100)) for _ in range(n_patients)]
# 医院位置,tuple (x,y)
hospitals_loc = [(randint(0, 100), randint(0, 100)) for _ in range(n_hospitals)]
# 病人严重等级 1~5
patients_severity = [randint(1, 5) for _ in range(n_patients)]变量
约束满足问题由一组变量组成,这些变量必须以满足一组约束。
- 令I为医院的集合
- 令$J_i$为医院i的床位集合
- 令$K$为病人集合
定义变量的索引族:
![]()
如果在医院i中,床j由病人k取走,则$x_{ijk} = 1$。为了将医院的每一张床与一个病人联系起来,我们的目标是找到一组满足所有约束条件的变量。
我们可以将这些变量添加到模型中:
model = cp_model.CpModel()
x = {}
for i in range(n_hospitals):
for j in range(n_beds_in_hospitals[i]):
for k in range(n_patients):
x[(i,j,k)] = model.NewBoolVar("x(%d,%d,%d)" % (i,j,k))硬约束
硬约束定义了模型的目标。它们是必不可少的,如果它们得不到解决,就无法解决问题:
- 每张床上最多只能有一个人
- 每个人最多只能有一张床
让我们关注第一个硬约束。对于每家医院的每一张床,我:
- 要么有一个唯一的病人k,
- 要么床是空的。
因此,可以用以下方式表示:
我们的求解器是一个组合优化求解器,它只能处理整数约束。因此,必须转化为一个整数方程:
这个不等式可以加到我们的模型中。
# 每张床最多只能住一个人
for i in range(n_hospitals):
for j in range(n_beds_in_hospitals[i]):
model.Add(sum(x[(i,j,k)] for k in range(n_patients)) <= 1)接下来,第二个硬约束:对于每个患者k:
- 要么他在一个唯一的病床上j在一个唯一的医院i
- 要么他在家。
同理,可以转化为一个整数不等式:
最后,可以将此约束添加到模型中。
# 每个人最多只能睡一张床
for k in range(n_patients):
inner_sum = []
for i in range(n_hospitals):
inner_sum.append(sum(x[(i,j,k)] for j in range(n_beds_in_hospitals[i])))
model.Add(sum(inner_sum) <= 1)软约束
接下来是软约束。这些都是非常需要的:我们的解决方案必须尽可能满足它们,但它们不是找到解决方案的必要条件:
- 每个病人都应该躺在床上
- 每个人都应该由最近的医院处理
- 病床不足时,应先处理病情严重的病人
当硬约束被建模为等式或不等式时,软约束是最小化或最大化的表达式。
设Ω为满足硬约束的所有解的集合。
![]()
每一个病人都应该被安排在一张床上,这意味着最大限度地增加被占用的床的数量。
每个人都应该由最近的医院处理,以尽量减少每个病人与其指定医院之间的距离。
如果没有足够的床位,应首先处理病情严重的病人,以最大限度地提高所有处理病人的总严重程度。通过表示sev(k)患者k的严重程度:
然后我们可以将所有软约束简化为一个目标:
需要注意的是:这些软约束没有相同的定义域。
- 患者最大化约束范围从0到n,其中n是患者数,
- 病情严重性限制范围从0到5n
- 距离约束范围从0到所有i和k的最大欧几里得距离。
考虑到所有这些约束具有相同的优先级,我们必须定义惩罚因子来平衡不同的约束。
下面是相应的代码:
# 整数的距离函数
idist = lambda xy1, xy2: int(((xy1[0]-xy2[0])**2 + (xy1[1]-xy2[1])**2)**0.5)
gain_max_patients = 140
gain_severity = int(140/5)
gain_distance = -1
#最大化的目标
soft_csts = []
for i in range(n_hospitals):
for j in range(n_beds_in_hospitals[i]):
for k in range(n_patients):
factor = \
gain_max_patients \
+ gain_distance * idist(hospitals_loc[i], patients_loc[k]) \
+ gain_severity * patients_severity[k]
soft_csts.append(factor * x[(i,j,k)])
model.Maximize(sum(soft_csts))求解
现在我们可以启动求解器了。它将试图在指定的时间限制内找到最优解。如果无法找到最优解,则返回最近的次优解。
solver = cp_model.CpSolver()
solver.parameters.max_time_in_seconds = 60.0
status = solver.Solve(model)在我们的例子中,求解器在2.5秒内返回一个最优解。
结论
要创建这个解决方案,只需要1小时的研究和30分钟的编程。
如果使用深度学习,要进行几天的数据清理,至少一天测试不同的架构,另一天进行训练。
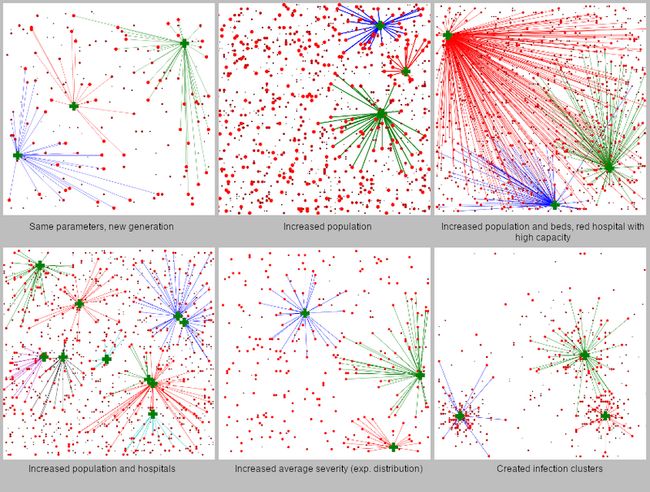
此外,如果模型良好,CP-SAT模型是非常健壮的。下面是不同模拟参数的结果。结果在许多不同的情况下仍然是一致的,随着模拟参数的增加(3000名患者,1000张病床),解决方案推断只需不到3分钟。
当然,csp几乎不适用于计算机视觉和NLP等主题,在这些主题中,深度学习有时是最好的方法。然而,在物流、调度和计划方面,这往往是可以实现的方法。
深度学习的炒作激发了一些人尝试一些疯狂的举动来获得认可。有时,最好还是通过阅读几篇关于你正在研究的问题的调查报告再想想你应该如何解决。
引用
[1] Jingchao Chen, Solving Rubik’s Cube Using SAT Solvers, arXiv:1105.1436, 2011.
[2] Biere, A., Heule, M., and van Maaren, H. Handbook of satisfiability, volume 185. IOS press, 2009a
[3] Knuth, D. E., The art of computer programming, Volume 4, Fascicle 6: Satisfiability. Addison-Wesley Professional, 2015
[4] Vipin Kumar, Algorithms for constraint-satisfaction problems: a survey, AI Magazine Volume 13, Issue 1, 1992.
原文链接:https://towardsdatascience.co...
欢迎关注磐创AI博客站:
http://panchuang.net/
sklearn机器学习中文官方文档:
http://sklearn123.com/
欢迎关注磐创博客资源汇总站:
http://docs.panchuang.net/