线段树和树状数组学习笔记

    学习了一周的线段树和树状数组，深深地体会到了这每种操作几乎都是 \(O(logN)\) 级别的数据结构的美，但是做起题来还是相当痛苦的（特别是一开始只会模板的时候，很难灵活运用线段树的性质）。还好有雨巨大神带入门，视频讲解十分直观（b站上也有很多介绍线段树的视频），不用像以前一样看各种博客题解入门。但是我现在就是在写博客了，希望能尽可能将我目前理解的知识整理出来，毕竟能让别人看懂（网上已经这么多关于线段树和树状数组的文章你还能找到我，相信我，你没选错），才说明自己也是真的懂了(虽然我还有好多不懂 \(QAQ\))。全文篇幅较长，细心理解一定会有收获的♪(^∇^*)。

线段树

一些概念

    线段树是一种二叉搜索树，每一个结点都是一个区间（也可以叫作线段，可以有单点的叶子结点），有一张比较形象的图如下（侵删）：

    可以看出，线段树除根结点外的其他节点，都由其父节点二分长度得到，这种优秀的性质使得我们可以把它近似看成是一棵完全二叉树。而完全二叉树可以用一个数组表示：设根节点下标为 \(now\) （在代码中我习惯用 \(now\) 表示当前节点， \(ls(now)\) 表示左孩子结点， \(rs(now)\) 表示右孩子结点），则:

\[ls(now) = now*2,rs(now) = now*2+1 \]

    这样就可以快速得到孩子的下标，根节点的下标为1，从上到下，从左往右编号既可将一颗线段树存入小巧的数组里了，不用烦人的指针。一般我会把左孩子和右孩子写到宏定义去，让代码更简洁，并且使用位运算，即:

\[ls(now) = now<<1,rs(now) = now<<1|1 \]

   这是等效的写法，同时我们要获得中间值，来二分 \(now\) 结点，同样我用了宏定义:

\[mid = (l+r)/2 \]

    \(l\) 和 \(r\) 是 \(now\) 的左右边界，即它所能管理（覆盖）的范围，明确这一点非常重要。线段树有很多种写法，我看的很多代码都是把 \(l\) 和 \(r\) 写在线段树节点的结构体里面，我习惯是用传参数的方法（因为带我入门的雨巨就是这样写的。其实两种写法都是可以的，看个人习惯，最后熟练一种即可，但是另一种也要看得懂）。左孩子的左边界还是 \(l\) , 右边界变成了 \(mid\) ；右孩子的左边界变成 \(mid+1\) ,右边界是 \(r\) 。这样就可以递归建树了。
   这个线段树数组的大小也是要注意（经常 \(RE\) 的地方），要开4倍的数组，就是说一个长度为10的区间，得开到40的数组。一般题目数据的范围都是在 \(10^5\) 的量级。有时数据范围过大，还可以用离散化解决它，这在后面的博客中会讲到。

能解决什么问题

   线段树能解决超多有关区间的问题，还有一些不这么明显的区间问题（废话）。像什么单点修改，单点查询，区间修改，区间查询都不在话下，应用范围比树状数组广，变通性极强（树状数组能解决的问题线段树都能解决，但是后者能解决的一些问题树状数组还是搞不了的，但是树状数组时空常数小，代码量少，还不容易写错）。线段树可以区间维护区间和、区间乘，区间根号，区间最大公因数，连续的串长度等、区间最值操作等。这里我给出一个洛谷题单和一个牛客题单，我也是刚刚刷完了这些题，质量都很高。

• 题单一：洛谷【数据结构2-2】线段树与树状数组
• 题单二：牛客算法竞赛入门课第九节(线段树)习题

   我是先做牛客的再去做洛谷的，顺序没什么。牛客题解比较少，需要自行百度理解（摘自牛客的一些比赛的比较多），洛谷质量就很高，题解丰富，做法也很多。可以先去做掉洛谷的四道模板题（线段树两道，树状数组两道，你还会发现线段树其实有三道模板题，模板三理解起来比较困难，建议先刷完前面的题再去攻克，不然很可能会自闭（我坦白了，我已经自闭了））。写完这篇总结后我会挑一些比较好的题再写一篇博客，算是题解总结吧。

建树、修改和查询

   题目一：P3372 【模板】线段树 1
   我们从模板题入手，题目中的两个操作正是线段树很经典的操作：区间修改和区间查询。我们思考以下几种做法：
   ① 如果让我们暴力地修改区间每一个值，再暴力查询区间的每一个值，修改和暴力都是 \(O(n)\) ，加上 \(m\) 次操作,总的时间复杂度就是 \(O(nm)\) 的，必定 \(TLE\) 。
   ② 预处理前缀和，进行离线操作。每次修改为 \(O(n)\) ，查询为 \(O(1)\) ，时间复杂度依旧是 \(O(nm)\) ，还是会 \(TLE\) 。
   ③ 以上操作的瓶颈都每次操作时间复杂度都是 \(O(n)\) ，这时我们想起了每次操作都是 \(O(logn)\) 线段树, 总的时间复杂度就是 \(O(mlogn)\) , \(AC\) 了。
   开始介绍之前，先交代一下线段树结构体：

const int maxn = 1e5+5;
struct node{
    ll sum,lazy; //sum为区间和，lazy为懒标记
}t[maxn<<2];   //开四倍空间

   区间和就不用说了，重点讲一下线段树 \(O(logn)\) 操作的关键：懒标记 \(lazy\) 。懒标记就是懒，将对区间操作的命令不立刻执行，而是到万不得已的时候才执行下去，否则就继续“偷懒”，将命令继续压在自己手上，不往自己孩子传。什么时候可以不往孩子节点传下去（即偷懒）呢？如果此时要修改的区间范围已经囊括了当前节点能管理的范围，那我就把这个命令直接在当前节点消化掉，不必再通知孩子也要执行这个命令了。
   举个栗子，比如我命令 \([1,10]\) 区间全部给我加 \(10\) ，到 \([1,10]\) 这个节点的时候，\([1,10]\) 正好包含住我管理的区间，那我直接给它的懒标记加上 \(10\) ，给区间和加上 \(100\) ,美滋滋地结束了任务，孩子们甚至不用知道这件事。下次如果要查询 \([1,10]\) 的区间和的话，我直接在 \([1,10]\) 这个节点返回就好了，因为它已经修改正确了。但是很多时候命令的区间是多个节点的并集区间。如果接下来我要 \([4,7]\) 这个区间加 \(5\) ，这个区间是 \([4,5]\) 和 \([6,7]\) 这两个节点的并，你可能会说这不就是在这两个节点打上标记就完事了吗？可事实上你之前在 \([1,10]\) 打上了懒标记，这个会影响 \([4,5]\) 和 \([6,7]\) 的区间和，而它的影响因为上次偷懒还没传下去呢，实际上 \([4,5]\) 和 \([6,7]\) 的懒标记应该打上 \(15\) 才对。那我们怎么亡羊补牢呢？诶，这需要 \(pushdown\) 函数帮忙啦，先卖个关子，先来讲讲怎么建树和修改。

建树build

   先给出代码，四行建树。

void build(int now,int l,int r){
    if(l == r) { cin>> t[now].sum ; return;}
    build(ls,l,mid);
    build(rs,mid+1,r);
    t[now].sum = t[ls].sum + t[rs].sum;
}

    \(now\)是当前节点的数组下标，\(l\) 和 \(r\) 是它所管辖的范围，如果 \(l\) 和 \(r\) 相等，说明到了叶子节点，也就是单点的情况，这时就直接读入数据好了，只有一个元素，区间和肯定就是它本身了，注意之后要返回，因为它不可再细分了；否则，将管辖范围一刀两半，利用类似完全二叉树的性质，递归建立左子树 \(ls\) 和右子树 \(rs\),这是我的宏定义（你可以修改各个变量名，很多人习惯用 \(p\) 代表当前节点，我比较直接就用 \(now\) 了）：

#define ls now<<1
#define rs now<<1|1
#define mid (l+r)/2

   建树代码最后一行是关键，也是线段树建树的精髓，我们一般将这句话写在一个函数 \(pushup\) 里面，与 \(pushdown\) 正好对应。在这里，它在递归返回时，左右子树已经建好了，要将它们的区间和信息整合到根节点，这里直接累加即可，不必成单独一个函数。但是当要维护的信息量很多时，因为这个 \(pushup\) 后面还会调用，我们会将它单独写成一个函数以减少代码量，降低维护成本。
这里的 \(pushup\) 代码可以写成：

void pushup(int now){
    t[now].sum = t[ls].sum + t[rs].sum;
}

   建树完毕，总结一下：
   1.先写递归返回条件 \(l == r\) 。
   2.递归左右子树 。
   3.合并两子树 \(pushup\) 。

修改update

   同样先给出代码：

void update(int now, int l, int r, int x, int y, int value){
    if(x <= l && r <= y) {
       t[now].lazy += value;
       t[now].sum += (r - l + 1) * value;
       return;
    }
    if(t[now].lazy)  pushdown(now,r-l+1);  
    //懒标记下传，与本次修改的信息无关，只是清算之前修改积压的懒标记
    if(mid >= x) update(ls, l, mid, x, y, value);
    if(mid < y) update(rs, mid + 1, r, x, y, value);
    pushup(now);
}

   前三个参数是固定参数，只与线段树本身有关，可以无脑打上，后三个参数在本题的意义为将 \(x\) 到 \(y\) 区间上每个值加上 \(value\) （可正可负）。
   首先我们还是得先写递归返回条件：如果要修改的区间满足 \([l,r]\in[x,y]\) ，也就是说已经涵盖了本区间了，那我就没有必要再将修改信息往下传了，在我这里修改就可以了嘛。所以我们偷个懒，打上标记，给区间和加上增量，搞定，返回。但是如果要修改的区间是 \([l,r]\) 的一部分，就要像之前我们说的，要执行神秘的 \(pushdown\) 操作了，即将懒标记下传。这里特别要注意的是，本次下传懒标记和这次修改没有任何关系，从传递的参数也可以看出来与后三个参数无关，它的作用就是清算之前偷懒造成的影响。来看看这个重要的 \(pushdown\) 代码

void pushdown(int now,int tot){
    t[ls].lazy += t[now].lazy;        //懒标记给左孩子
    t[rs].lazy += t[now].lazy;        //懒标记给右孩子
    t[ls].sum += (tot - tot/2) * t[now].lazy;  //区间和加上懒标记的影响，注意范围
    t[rs].sum += (tot/2) * t[now].lazy;
    t[now].lazy = 0;  //记得懒标记下传后清0
}

  新参数 \(tot\) 表示当前节点管辖区间的范围大小，注意左孩子管辖范围为 \(tot-tot/2\) ，右孩子是 \(tot/2\) ，在加区间和的时候要小心。把之前偷懒的部分传给孩子后，偷懒记录就清零啦（摸鱼成功）。这时不要不放心继续 \(pushdown\) 左孩子和右孩子，这是没有必要的，因为之后我们还会继续 \(update\) 左子树和右子树（看上上个代码），如果有需要就会进行 \(pushdown\)，没有需要就继续偷懒。这样就能保证完整的 \(update\) 操作是 \(O(logn)\) 的。注意，递归左右子树之前先判断需不需要递归。分两种情况，如果你要修改的部分完全在左子树，就没有必要修改右子树；同理亦是如此。这样可以防止无限递归了（如果在测试样例的时候发现不出结果，大概率就是这里没写对）。
   修改完毕，总结一下：
   1.先写递归返回条件 \(x <= l ~\&\&~ r <= y\) ,执行偷懒操作。
   2.如果当前节点有懒标记积压，执行 \(pushdown\) 操作，先清算之前的账。
   3.根据条件判断递归哪棵子树（可能两棵都会修改）进行修改。
   4.合并两子树 \(pushup\) 。

查询query

  最后一部分就是查询了，与修改操作其实比较类似：

ll query(int now, int l, int r, int x, int y){
    if(x <= l && r <= y) return t[now].sum;
    if(t[now].lazy) pushdown(now,r-l+1);
    ll ans = 0;
    if(mid >= x)  ans += query(ls, l, mid, x, y);
    if(mid < y)  ans += query(rs, mid + 1, r, x, y);
    return ans;
}

  你可能也发现查询操作比较好理解，最不容易写错，也是写的比较开心的一部分了。要注意的还是记得 \(pushdown\) ，因为要查询的区间可能是当前节点的某个孩子，如果不把之前的懒标记下传，查询会出错。递归返回区间和就行，并不用 \(pushup\) （查询不会修改当前节点的值）。
   查询完毕，总结一下：
   1.先写递归返回条件 \(x <= l ~\&\&~ r <= y\) ,返回区间和信息即可。
   2.如果当前节点有懒标记积压，执行 \(pushdown\) 操作，先清算之前的账。
   3.根据条件判断递归子树进行查询。
   4.合并两子树查询结果并返回。

完整代码：

#include
using namespace std;
#define For(i,sta,en) for(int i = sta;i <= en;i++)
#define speedUp_cin_cout ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);
#define ls now<<1
#define rs now<<1|1
#define mid (l+r)/2
typedef long long ll;
const int maxn = 1e5+5;
int n,m;
struct node{
    ll sum,lazy; //sum为区间和，lazy为懒标记
}t[maxn<<2];

void pushup(int now){
    t[now].sum = t[ls].sum + t[rs].sum;
}

void build(int now,int l,int r){
    if(l == r) { cin>> t[now].sum ; return;}
    build(ls,l,mid);
    build(rs,mid+1,r);
    pushup(now);
}

void pushdown(int now,int tot){
    t[ls].lazy += t[now].lazy;        //懒标记给左孩子
    t[rs].lazy += t[now].lazy;        //懒标记给右孩子
    t[ls].sum += (tot - tot/2) * t[now].lazy;  //区间和加上懒标记的影响，注意范围
    t[rs].sum += (tot/2) * t[now].lazy;
    t[now].lazy = 0;  //记得懒标记下传后清0
}

void update(int now, int l, int r, int x, int y, int value){
    if(x <= l && r <= y) {t[now].lazy += value; t[now].sum += (r - l + 1) * value;return;}
    if(t[now].lazy)  pushdown(now,r-l+1);  //懒标记下传，与本次修改的信息无关，只是清算之前修改积压的懒标记
    if(mid >= x) update(ls, l, mid, x, y, value);
    if(mid < y) update(rs, mid + 1, r, x, y, value);
    pushup(now);
}

ll query(int now, int l, int r, int x, int y){
    if(x <= l && r <= y) return t[now].sum;
    if(t[now].lazy) pushdown(now,r-l+1);
    ll ans = 0;
    if(mid >= x)  ans += query(ls, l, mid, x, y);
    if(mid < y)  ans += query(rs, mid + 1, r, x, y);
    return ans;
}

int main(){
    speedUp_cin_cout//加速读写
    cin>>n>>m;
    build(1,1,n);  //建树顺便读入，省一个数组
    int op,l,r,d;
    For(i,1,m){
        cin>>op;
        if(op == 1) {  // l 到 r 加上 d
            cin>>l>>r>>d;
            update(1, 1, n, l, r, d);
        }else {
            cin>>l>>r;     //查询 l 到 r 的值
            cout << query(1, 1, n, l, r) << endl;
        }
    }
    return 0;
}

  干掉这题就可以去做P3373 【模板】线段树 2了,这题会提升你对懒标记的理解，\(pushdown\) 的懒标记下传处理变得有些复杂。因为它要同时维护区间加标记和区间乘标记，区间乘标记会同时影响区间加标记和区间乘标记，想要 \(AC\) 还是得细心理解乘和加的关系。

树状数组

一些概念

  树状数组，顾名思义，就是像一棵树的数组。其实它和树关系不太大，实际操作时有类似在树上节点的跳跃的过程，但是在写代码的时候它也不过是个一维数组而已，和线段树还是有一点点像的，不过是将线段树的一些精华部分充分压缩了。来，让我们看看传说中的树状数组长啥样（纯手工，不要在意细节）：

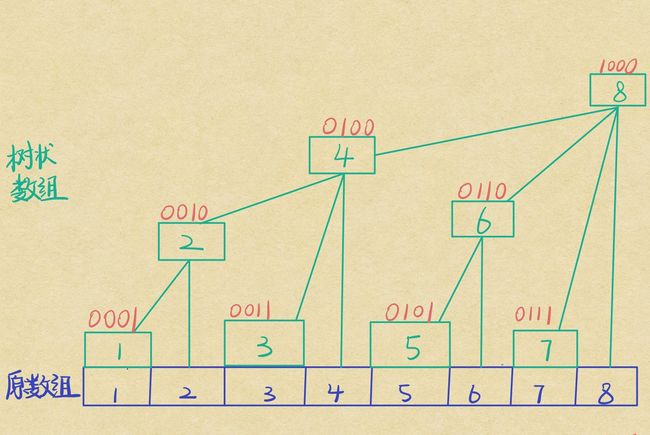
  绿油油的就是树状数组啦，它头上红色的是这个下标对应的二进制,最底下的就是原数组了。直觉告诉你，他们之间隐约存在某些关系。你可能会觉得这里一共有两个数组，还有一堆连线，要维护起来是不是很麻烦啊。其实他们可以只用一个一维数组存储所有信息，而其中关键的纽带就是二进制。
  我们设原数组为 \(A\) ,树状数组为 \(T\) ,定义连线的意义就是一个节点能管辖的范围。例如 \(T_1\) 能直接管辖管辖到 \(A_1\) , \(T_2\) 能管辖到 \(T_1\) （间接管辖到 \(A_1\)）和 \(A_2\), \(T_4\) 能管辖到 \(T_2\) 、\(T_3\) 和 \(A_4\) ,亦即 \(T_4\) 能管辖到原数组 \(A_1\) 、\(A_2\) 、\(A_3\)和 \(A_4\) ...以此类推，\(T_8\) 能管辖到原数组所有值。所以，我们只要存储 \(T_1\) , \(T_2\) 的值，原数组中 \(A_2\) 可以由这两者相减得到；同理， \(A_5\) 、\(A_6\) 、\(A_7\)和 \(A_8\) 的总和可以由 \(T_8\) 减去 \(T_4\) 得到。所以，我们只要保留树状数组，原数组的信息完全可以由树状数组维护出来，并且轻松知道任意一个区间的信息和。
  那么新的问题出现了，我们如何知道谁管辖谁，他们之间有什么联系吗？这时，奇妙的二进制出现了。观察树状数组头上的二进制，看出被管辖者与管辖着之间在二进制上的联系了吗？揭晓答案，被管辖者加上 \(2^k\)，\(k\) 为被管辖者二进制末尾零的个数，即可得到管辖着的二进制！举个栗子，\(T_2\) 的二进制为 \(0010\) ,加上 \(2^1（0010）\) ,得到 \(0100\) ,即 \(T_4\) 。我们一般将 \(2^k\) 写成一个函数叫 \(lowbit\) ，树状数组下标 \(x\) 与它的 \(lowbit\) 如下关系：

\[lowbit = x\&(-x) \]

  证明其实没必要，会用就行，这涉及到负数在计算机中存储的形式，可以自己证一下。

修改update

  P3374 【模板】树状数组 1
  树状数组完全不用像线段树一样需要一个函数来建树，声明了一个一维数组（数组大小等于数据量即可，不用开多几倍）直接就可以进行修改查询等操作了。它的修改函数代码非常短，而且形式几乎不变。

void update(int now,int value){
    while(now <= n){
        t[now] += value;
        now += lowbit(now);
    }
}

  三行循环就结束了，线段树自愧不如。这个函数的意义是在原数组的 \(now\) 的下标位置加上 \(value\) ,循环的终点是大于了树状数组的下标范围 \(n\) 。它是怎么通过加上 \(lowbit\) 实现的呢？来看下面这张图：

  假如我们要修改原数组 \(5\) 这个位置的值，能管辖到它的只有 \(T_6\) 和 \(T_8\) 。因为我们要求区间和，所以 \(T_6\) 和 \(T_8\) 要都加上 \(T_5\) 修改后的值才行。这时我们用一个 \(lowbit\) 在循环中从 \(T_5\) 跳到 \(T_6\)，再跳到 \(T_8\) ，一气呵成。这样，单点修改操作就完成啦。

查询query

  查询操作永远是和修改操作配套的，一切修改的目的都是为了查询的方便。既然修改代码这么短小精悍，那么查询代码就更加小巧了，请看：

ll query(int now){
    ll ans = 0;  //long long 类型的答案
    while(now){
        ans += t[now];
        now -= lowbit(now);
    }return ans;
}

  代码的意义是查询原数组从 \(1\) 到 \(now\) 的前缀和，即从 \(A_1\) 到 \(A_{now}\) 的和。注意这时我们的 \(lowbit\) 操作变成了减，而之前修改操作是加。原理也可以看图说明：

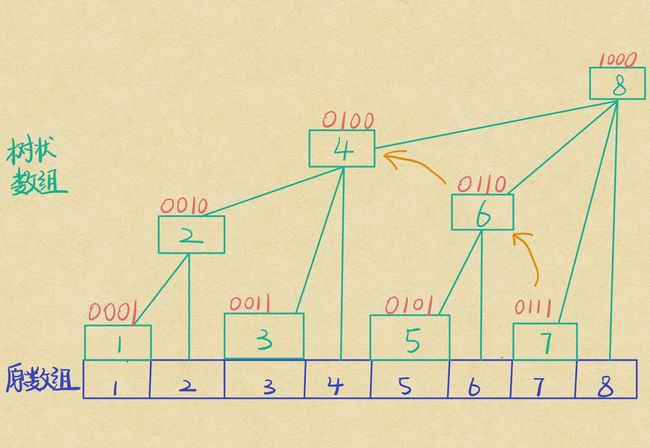
  图中我们查询的是 \(1\) ~ \(7\) 的前缀和，我们先加上 \(T_7\) 的答案，再减去它的 \(lowbit\) 跳到 \(T_6\) ，最后跳到 \(T_4\) ,因为 \(T_6\) 和 \(T_4\) 在前面的修改操作中已经维护出了自己管辖区域的区间和，都加上就是 \(1\) ~ \(7\) 的前缀和了。
  知道了前缀和，区间和其实就很容易了，假如我们要求 \([x,y]\) 的区间和，其实就是 \(query(y)-query(x-1)\) ，注意是 \(x-1\) ，要自己想一想，这个地方总是容易被忽略。

完整代码

#include
using namespace std;
#define For(i,sta,en) for(int i = sta;i <= en;i++)
#define speedUp_cin_cout ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);
#define lowbit(x) x&(-x)
typedef long long ll;
const int maxn = 5e5+5;
int t[maxn],n,m,num;

void update(int now,int value){
    while(now<=n){
        t[now]+=value;
        now += lowbit(now);
    }
}

ll query(int now){
    ll ans = 0;  //long long 类型的答案
    while(now){
        ans += t[now];
        now -= lowbit(now);
    }return ans;
}

int main(){
    speedUp_cin_cout
    cin>>n>>m;
    For(i,1,n) {
        cin>>num;
        update(i,num);
    }int op,x,y;
    For(i,1,m){
        cin>>op>>x>>y;
        if(op == 1) update(x,y);
        else cout<

  是不是比线段树短多了。这是单点修改，区间查询。洛谷还有道P3368 【模板】树状数组 2，是区间修改，单点查询。这就需要差分的思想了。所谓的差分，其实就是后一项与前一项的差，对于第一项而言，\(a[0] = 0\) 。设数组 \(a[~]=\{1,9,3,5,2\}\) ，那么差分数组\(t[~]=\{1,8,-6,2,-3\}\) ，即 \(t[i]=a[i]-a[i-1]\) ,那么 $$a[i]=t[1]+...+t[i]$$
这不就是前缀和吗?以对原数组的区间修改，单点查询就是在其差分数组上单点修改，区间查询。但是要注意的是，这里的单点其实是要修改两个点。例如我们如果要让 \([2,3]\) 区间加上 \(4\) ,首先是要修改差分数组上的 \(t[2] +4\)， 然后还要修改 \(t[4]-4\) ,这也是很好理解的，毕竟 \([2,3]\) 区间比其他区间突出了一块，整体提高了 \(4\) ，而其他的区间的差分关系并没有被改变。这样，我们也可以很愉快地 \(AC\) 这道题了。

还有一些话

  做模板题是快乐的（除了P6242 【模板】线段树 3）,但是实际应用起来是比较头疼的。因为线段树和树状数组灵活性很高，可以解决很多看似无法下手的问题，但是要维护的信息多得容易摸不着头脑（不知道为什么这样做就可以了），逻辑关系环环相扣，时不时就得感叹一下“妙”。这些都得做更多的题来体会了。还有不要死记模板，要清楚知道每一步的作用，很多时候一些顺序会颠倒，来解决不同的问题，这是需要警惕的。
  如果觉得对你理解有帮助的希望给我点个赞哦，ο(=•ω＜=)ρ⌒☆