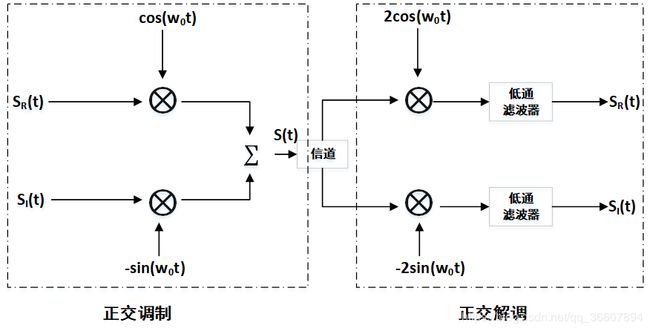
正交调制与解调
网上查到的关于正交信号调制解调的内容不多,大多数介绍也忽略了理论推导,今天突然碰到了相关问题需要理解这个知识,发现自己之前本科的高频和通信原理学的真是浅显糊弄,翻了好半天本科的各种课本才搞清楚,特此记录下来,不要老是摸鱼。
(一)上图的解释性推导
调制和解调是本科时高频课程的学习内容,所以我们应该和必须知道,乘法器是实现调制和解调的关键组件!!!
此外,关于为啥要调制,那是因为电磁波理论告诉我们,天线尺寸是被辐射信号波长的十分之一或更大,信号才能被有效辐射实现无线通信。如果要辐射语音信号(300-3400Hz)出去实现传输,则至少天线需要几十公里( λ = c f = 3 ∗ 1 0 8 m / s 300 H z = 1000 k m , 1000 k m ∗ 0.1 = 100 k m \lambda=\frac cf=\frac{3*10^8m/s}{300Hz}=1000km,1000km*0.1=100km λ=fc=300Hz3∗108m/s=1000km,1000km∗0.1=100km),显然是不可能实现的,所以必须把包含大量低频成分的基带信号搬到更高的频段,这种线性的搬移就是线性调制,有AM,DSB,SSB,VSB等,不再细说。此外,搬移频率也是为了便于接收机识别自己要接收的信号。
如图,一路信号的载波是 c o s ( w 0 t ) cos(w_0t) cos(w0t),另一路信号的载波是 − s i n ( w o t ) -sin(w_ot) −sin(wot),载波幅度在这里均为1,两个载波相位相差 9 0 o 90^o 90o,完全正交。
合成信号:
(1) s ( t ) = s R ( t ) c o s ( w 0 t ) − s I ( t ) s i n ( w 0 t ) s(t)=s_R(t)cos(w_0t)-s_I(t)sin(w_0t)\tag1 s(t)=sR(t)cos(w0t)−sI(t)sin(w0t)(1)
根据傅里叶变换的常用公式:
(2) c o s ( w 0 t ) ⟺ π [ δ ( w − w 0 ) + δ ( w + w 0 ) ] cos(w_0t)\Longleftrightarrow \pi[\delta(w-w_0)+\delta(w+w_0)]\tag2 cos(w0t)⟺π[δ(w−w0)+δ(w+w0)](2)
(3) s i n ( w 0 t ) ⟺ π j [ δ ( w − w 0 ) − δ ( w + w 0 ) ] sin(w_0t)\Longleftrightarrow \frac{\pi}{j}[\delta(w-w_0)-\delta(w+w_0)]\tag3 sin(w0t)⟺jπ[δ(w−w0)−δ(w+w0)](3)
(4) f ( t ) h ( t ) ⟺ 1 2 π F ( w ) ∗ H ( w ) f(t)h(t)\Longleftrightarrow \frac{1}{2\pi}F(w)*H(w)\tag4 f(t)h(t)⟺2π1F(w)∗H(w)(4)
得到:
(5) s R ( t ) c o s ( w 0 t ) ⟺ 1 2 [ S R ( w − w 0 ) + S R ( w + w 0 ) ] s_R(t)cos(w_0t)\Longleftrightarrow \frac12[S_R(w-w_0)+S_R(w+w_0)] \tag5 sR(t)cos(w0t)⟺21[SR(w−w0)+SR(w+w0)](5)
(6) − s I ( t ) s i n ( w 0 t ) ⟺ j 2 [ S I ( w − w 0 ) − S I ( w + w 0 ) ] -s_I(t)sin(w_0t)\Longleftrightarrow \frac j2[S_I(w-w_0)-S_I(w+w_0)] \tag6 −sI(t)sin(w0t)⟺2j[SI(w−w0)−SI(w+w0)](6)
(7) S ( w ) = 1 2 [ ( S R ( w − w 0 ) + S R ( w + w 0 ) ) + j ( S I ( w − w 0 ) − S I ( w + w 0 ) ) ] S(w)=\frac12[(S_R(w-w_0)+S_R(w+w_0))+j(S_I(w-w_0)-S_I(w+w_0))]\tag7 S(w)=21[(SR(w−w0)+SR(w+w0))+j(SI(w−w0)−SI(w+w0))](7)
调制到此结束,继续推导解调:
合成信号 s ( t ) s(t) s(t)经过信道产生的畸变,失真暂不考虑。
2 s ( t ) c o s ( w 0 t ) ⟺ S ( w − w 0 ) + S ( w + w 0 ) = 2s(t)cos(w_0t)\Longleftrightarrow S(w-w_0)+S(w+w_0)= 2s(t)cos(w0t)⟺S(w−w0)+S(w+w0)=
1 2 [ ( S R ( w − 2 w 0 ) + S R ( w ) + S R ( w ) + S R ( w + 2 w 0 ) ) + j ( S I ( w − 2 w 0 ) − S I ( w ) + S I ( w ) − S I ( w + 2 w 0 ) ) ] \frac12[(S_R(w-2w_0)+S_R(w)+S_R(w)+S_R(w+2w_0))+j(S_I(w-2w_0)-S_I(w)+S_I(w)-S_I(w+2w_0))] 21[(SR(w−2w0)+SR(w)+SR(w)+SR(w+2w0))+j(SI(w−2w0)−SI(w)+SI(w)−SI(w+2w0))]
经过低通滤波器,滤除 2 w 0 2w_0 2w0的频率分量,则只剩
S R ( w ) S_R(w) SR(w)
经傅里叶反变换自然得到 s R ( t ) s_R(t) sR(t).
同理, − 2 s ( t ) s i n ( w 0 t ) ⟺ j [ S ( w − w 0 ) − S ( w + w 0 ) ] = -2s(t)sin(w_0t)\Longleftrightarrow j[S(w-w_0)-S(w+w_0)]= −2s(t)sin(w0t)⟺j[S(w−w0)−S(w+w0)]=
j 2 [ ( S R ( w − 2 w 0 ) + S R ( w ) − S R ( w ) − S R ( w + 2 w 0 ) ) + j ( S I ( w − 2 w 0 ) − S I ( w ) − S I ( w ) + S I ( w + 2 w 0 ) ) ] \frac j2[(S_R(w-2w_0)+S_R(w)-S_R(w)-S_R(w+2w_0))+j(S_I(w-2w_0)-S_I(w)-S_I(w)+S_I(w+2w_0))] 2j[(SR(w−2w0)+SR(w)−SR(w)−SR(w+2w0))+j(SI(w−2w0)−SI(w)−SI(w)+SI(w+2w0))]
经过低通滤波器,滤除 2 w 0 2w_0 2w0的频率分量,则只剩
S I ( w ) S_I(w) SI(w)
经傅里叶反变换自然得到 s I ( t ) s_I(t) sI(t).
(二)复数表示
上图的两路信号分别称为同相(In-Phase)分量信号和正交(Quadrature)分量信号。合成信号 s ( t ) s(t) s(t)叫做正交调制信号。
如果两路信号中除了时间参数外还有未知参数如振幅,频率,相位,则它们是随机过程 。
假设两个分量信号是零均值的联合平稳的实过程,则合成信号就是调制过程(实过程):
(1) s ( t ) = s R ( t ) c o s ( w 0 t ) − s I ( t ) s i n ( w 0 t ) s(t)=s_R(t)cos(w_0t)-s_I(t)sin(w_0t)\tag1 s(t)=sR(t)cos(w0t)−sI(t)sin(w0t)(1)
(1)是正交表达式。下面写出三角形式,也叫包络相位表达式:
(2) s ( t ) = r ( t ) c o s [ w 0 t + θ ( t ) ] s(t)=r(t)cos[w_0t+\theta(t)]\tag2 s(t)=r(t)cos[w0t+θ(t)](2)
则振幅和相位都是随机过程:
(3) r ( t ) = ( s R ( t ) ) 2 + ( s I ( t ) ) 2 , θ ( t ) = arctan s I ( t ) s R ( t ) r(t)=\sqrt{(s_R(t))^2+(s_I(t))^2},\quad \theta(t)=\arctan\frac{s_I(t)}{s_R(t)} \tag3 r(t)=(sR(t))2+(sI(t))2,θ(t)=arctansR(t)sI(t)(3)
振幅 r ( t ) r(t) r(t)是包络,相对于 s ( t ) s(t) s(t),它通常是慢变化的。
构造复过程:
(4) a ( t ) = s R ( t ) + j s I ( t ) = r ( t ) e j θ ( t ) a(t)=s_R(t)+js_I(t)=r(t)e^{j\theta(t)}\tag4 a(t)=sR(t)+jsI(t)=r(t)ejθ(t)(4)
a ( t ) a(t) a(t)是复包络。
显然有:
(5) s R ( t ) = r ( t ) c o s θ ( t ) , ( r e a l p a r t ) s_R(t)=r(t)cos\theta (t) ,(real \quad part)\tag5 sR(t)=r(t)cosθ(t),(realpart)(5)
(6) s I ( t ) = r ( t ) s i n θ ( t ) , ( i m a g i n a r y p a r t ) s_I(t)=r(t)sin \theta (t) ,(imaginary \quad part)\tag6 sI(t)=r(t)sinθ(t),(imaginarypart)(6)
再构造解析过程(实部是自己,虚部是自己的希尔伯特变换的复过程):
(7) z ( t ) = s ( t ) + j s ^ ( t ) z(t)=s(t)+j\hat s(t)\tag7 z(t)=s(t)+js^(t)(7)
代入