字符串的最长回文子串--manacher算法

预备知识：

字符串概念

回文子串概念

 

朴素算法：

通常我们熟知的求解字符串的最长回文字串的方法有以下两种算法：

1、O(n^2)枚举子串的左右两个端点->O(n)判断该子串是否为回文串：总复杂度O(n^3);

2、O(n)枚举每一个回文子串的中点(偶数长度类似，不做讨论)->O(n)向两端拓展：总复杂度O(n^2)。

然而在一般的算法竞赛中，O(n^2)复杂度求回文子串的算法是无法接受的，下面介绍一种在线性时间内求字符串的最长回文子串的算法--manacher算法。

 

manacher算法：

如果将上述算法2视为算法1的优化版本，那么manacher算法可视为算法2的优化版本。下面先分析算法2的不足之处。

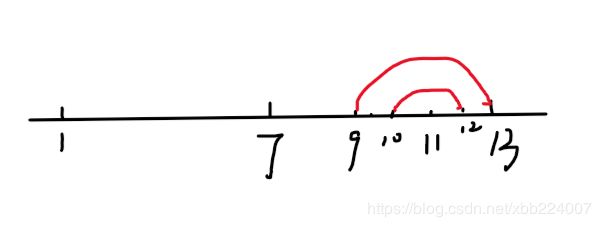
对于算法2我们会枚举每一个位置的中点，每次都从枚举点开始向两端拓展。比如下图中枚举了7作为中点，假设其两端最远拓展的长度为6，即字符串[1~13]为一个回文子串(并且13为当前向右拓展的最远距离)。当我们再枚举11作为中点时，我们会依次比较：(10，12)->(9，13)->......，这样的复杂度就是O(n^2)。然而实际上我们还需要对7为中点的子串进行这样的枚举吗?

其实是不需要的。

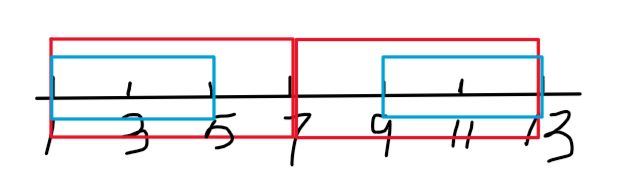
因为我们已经知道了[1~13]为一个回文子串了，也就是说子串[1~7]与[7~13]一样（下图红框所示）。那么子串[9~13]当然与对称位置的子串[1,5]一样（下图蓝框所示）。更本质一点就是<以11为中心的回文子串的情况>与<以3为中心的回文子串的情况>一致。而我们是已经求出来了<以3为中心的回文子串的情况>了的，故可以直接求解<以11为中心的回文子串的情况>。

说到这里貌似还有点问题，因为如果<以3为中心的回文子串的长度>为3呢?我们当然不能直接说[8~14]也是一个回文子串，因为14以后的情况还未知，也就是说后面的情况需要暴力地去匹配，所以说这还是一个暴力算法2333，不过好歹我们已经避免了一段比较了嘛~。由此我们可以归纳得到如下算法：

首先将上述过程一般化，设：

        ①mx为当前向右拓展的最远的下标(上面的13)；

        ②id为该拓展对应的中心点(上面的7)；

        ③对于已经枚举过的中心i，我们用p[i]表示<以i为中心最远能向两边扩展的“半径”长度(包括中心点，即最小为1)>。

        ④当前枚举的中心位置为x，那么其关于id的对称点为2id-x。

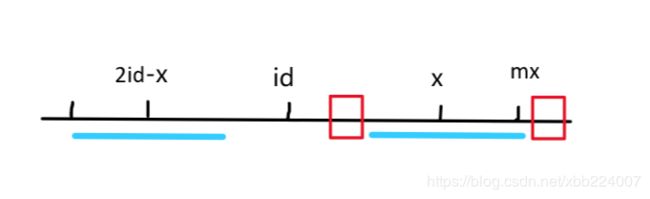
由上面的讨论可知，<以x为中心的回文子串能最长拓展的“半径”长度>至少为p[x]=min(p[2id-x]，mx-x)（下图中蓝色线条部分）。对于mx以后的情况还需要进行暴力地匹配（下图中红色框部分，继续更新p[x]）。如果匹配后发现<以x为中心的回文子串能向右拓展的最远的下标>大于mx，那么更新id与mx的值。再接着枚举x以后的点作为回文串中心。

现在还有一个小问题，那就是上述的过程都是在x=mx呢？首先直接令p[x]=1(因为x>=mx，则前面得到的回文子串的信息对于<以x为中心的回文串>起不到什么作用了)，然后暴力匹配以x为中心两边相同的字符的个数来更新p[x]，最后在更新id和mx。

这样一来按照上述的过程就可以更新所有的点的“拓展半径”了。至此就基本讲完了manacher算法了，不知道大家是否能看得明白(￣o￣) . z Z。

 

字符串的处理：

上面为什么说是基本讲完了呢？因为在实际应用的过程中，我们又会碰到一个问题。上述所有的过程都是建立在有一个id以及一个回文串中心x的基础上的，而实际上，当回文串长度为偶数时是没有中心字符的，这时候这么处理？

我们将任意两个字符之间以及字符串的首位均插入一个一样的字符(比如"#"，不会出现在给定的字符串即可)得到一个新的字符串，那么我们可以容易地发现如下事实：

①原来的偶数长度的回文串，可以对应对新字符串中一个以‘#’为中心的字符串；

②原来的奇数长度的回文串，可以对应对新字符串中一个以原字符为中心的字符串；

那么我们对新的字符串使用manacher算法，求出每一个下标的p[x]，更具p[]数组以及两个字符串回文串长度之间的对应关系就可以得到原字符串的最长回文串了。对应关系？——p[x]-1即为原字符串的回文串长度（举几个具体的例子就可以归纳了）。

这样一来，manacher算法就算是讲完了(￣▽￣)"。

 

复杂度分析：

本人也不怎么会算复杂度，但是介绍一个算法，总归是要解释以下才行的丫。这里的复杂度是这么将为O(n)的呢？考虑字符串中每一个字符的遍历次数，由于在mx左边的字符只会再被用来与其右边进行一次暴力的匹配，在加上每个字符在mx右边时一定会被匹配一次，那么一个字符被用来匹配的次数不会超过两次，所以总的时间复杂度是O(n)的(逃~)。

 

代码实现：

测试题目链接：hihoCode-1032-最长回文子串

//hihoCode 1032	最长回文子串
#include
#include
#include
#include
#include
using namespace std;
const int maxn=2e6+10;
char s[maxn],str[maxn];
int n,len1,len2,p[maxn];
void init(){
    len1=strlen(s);str[0]='#';
    for(int i=0;ii)p[i]=min(p[2*id-i],mx-i);
        else p[i]=1;
        for(;i>=p[i]&&str[i-p[i]]==str[i+p[i]];p[i]++);
        if(p[i]+i>mx)mx=p[i]+i,id=i;
        ans=max(ans,p[i]-1);
    }
    return ans;
}
int main(){
    scanf("%d",&n);
    for(int i=0;i

该代码是按照自己的理解完成的(实际上理解了原理后写起来真的没什么难度)，不保证结果的百分之百正确o，网上当然有十分优秀的板子，这里挂出来可以看个实现的具体过程。

 

总结：

字符串的基础知识，也是个特别简单的算法(实际上碰到地也不多::>_<::)。

更多灵活地运用还需要找其它具体的题目进行练习(以后可能续上？)。

比较少写这种介绍知识点的文章，有什么错误纰漏或者建议都欢迎提出来o。