Leetcode刷题全记录,每题都有长进(hot 100 438-739)
438 找到字符串中所有字母异位词
滑动窗口法
滑动窗口算法的思路是这样:
-
我们在字符串 S 中使用双指针中的左右指针技巧,初始化
left = right = 0,把索引闭区间[left, right]称为一个「窗口」。 -
我们先不断地增加
right指针扩大窗口[left, right],直到窗口中的字符串符合要求(包含了 T 中的所有字符)。 -
此时,我们停止增加
right,转而不断增加left指针缩小窗口[left, right],直到窗口中的字符串不再符合要求(不包含 T 中的所有字符了)。同时,每次增加left,我们都要更新一轮结果。 -
重复第 2 和第 3 步,直到
right到达字符串 S 的尽头。
这个思路其实也不难,第 2 步相当于在寻找一个「可行解」,然后第 3 步在优化这个「可行解」,最终找到最优解。左右指针轮流前进,窗口大小增增减减,窗口不断向右滑动。
用两个哈希表当作计数器解决。用一个哈希表 needs 记录字符串 t 中包含的字符及出现次数,用另一个哈希表 window 记录当前「窗口」中包含的字符及出现的次数,如果 window 包含所有 needs 中的键,且这些键对应的值都大于等于 needs 中的值,那么就可以知道当前「窗口」符合要求了,可以开始移动 left 指针了。
接下来直接看代码
首先是模板化的代码
dicP = {}
cur = {}
mark = 0
ans = []
for i in p:
dicP[i] = dicP.get(i, 0)+1
right = left = 0
while right < len(s):
if s[right] in dicP:
cur[s[right]] = cur.get(s[right], 0)+1
if cur[s[right]] == dicP[s[right]]:
mark += 1
right += 1
while mark == len(dicP):
if right-left == len(p):
ans.append(left)
if s[left] in dicP:
cur[s[left]] -= 1
if cur[s[left]] < dicP[s[left]]:
mark -= 1
left += 1
return ans
针对这道题目我们还可以优化,因为要求是连续的移位字符串,两个的哈希表必须一样,因此我们简化了一些判断。
class Solution:
def findAnagrams(self, s: str, p: str) -> List[int]:
res = []
n = len(s)
m = len(p)
window = {}
needs = {}
for i in p:
needs[i] = needs.get(i,0) + 1
left = right = 0
while right < n:
c = s[right]
if c not in needs:
window.clear()
left = right = right + 1
else:
window[c] = window.get(c,0) + 1
if right-left + 1 == m:
if window == needs:
res.append(left)
window[s[left]] -= 1
left += 1
right += 1
return res
代码里面有个巧妙之处在于,字典的初始化。采用了dic[i] = dic.get(i,0)+1在不存在键时返回0,并加一。实现了初始化。
用到这一思路的类似题目
494 目标和
还是老思路,看到返回具体数字不要求具体路径的,优先考虑dp方法。仔细分析这是一道类似背包问题的题目,还是两条路一边缩小数组,一边缩小目标值。类似背包问题,该类问题的dp设计为:dp[len(item)][target]也就是dp = [[0]*(target+1) for _ in range(len(item))]
- 状态:
dp[i][j]表示前i个元素组成j的数量 - 转移方程:
dp[i][j] = dp[i-1][j-nums] + dp[i+1][j+nums]其实对应了两种操作,一种是加上当前值,一种是减去当前值。这里其实需要特别思考数组的索引,我会在后面详细说。 - 初始状态:第一个状态单独设定,
+-nums标记为1即可,但是注意可能出现0的情况。 - 索引设计:这道题目可能会有
j-nums<0的情况,因此需要整个数组平移一下,数组长度变为2*sum(nums)+1
这道题目很难压缩状态,除非整体继续移动。
class Solution:
def findTargetSumWays(self, nums: List[int], S: int) -> int:
k = sum(nums)
if S>k:
return 0
dp = [[0]*(2*k+1) for _ in range(len(nums))]
dp[0][k-nums[0]] = 1
# k可能为0
dp[0][k+nums[0]] += 1
for i in range(1,len(nums)):
for j in range(0, 2*k+1):
if j-nums[i]>=0:
dp[i][j] += dp[i-1][j-nums[i]]
if j+nums[i]<=2*k:
dp[i][j] += dp[i-1][j+nums[i]]
return dp[-1][k+S]
还有一种很绝的做法,我还没想到这种算法的一般性作用。但是很妙。
原问题等同于: 找到nums一个正子集和一个负子集,使得总和等于target
我们假设P是正子集,N是负子集 例如: 假设nums = [1, 2, 3, 4, 5],target = 3,一个可能的解决方案是+1-2+3-4+5 = 3 这里正子集P = [1, 3, 5]和负子集N = [2, 4]
那么让我们看看如何将其转换为子集求和问题:
sum ( P) - sum(N) = target
sum( P) + sum(N) + sum( P) - sum(N) = target + sum( P) + sum(N)
2 * sum( P) = target + sum(nums)
因此,原来的问题已转化为一个求子集的和问题: 找到nums的一个子集 P,使得·sum( P) = (target + sum(nums)) / 2
class Solution(object):
def findTargetSumWays(self, nums, S):
## 绝了,具体思想看评论顶层
if sum(nums) < S or (sum(nums) + S) % 2 == 1: # 奇偶性不同也不可以
return 0
P = (sum(nums) + S) // 2 # sum(nums) + S一定是偶数
# dp[j] 表示能得正数组和为j的个数
dp = [0 for _ in range(P+1)]
dp[0] = 1 # 表示为添加这个数字时为0
# 采用了状态压缩的方法
for num in nums:
for j in range(P,num-1,-1): # 相当于判断了一下 if j>num-1,因为dp只增
dp[j] = dp[j] + dp[j - num] # 两种操作,添加该数字,或不添加
return dp[P]
这个方法太玄学了。
560和为K的子数组

看到题目的第一反应是采用滑动窗口的方法,但是有一个问题是存在负数在数组中,因此没办法判定何时动窗。
题目的解析给了一种前缀和的方法,还是基于对题目的理解得到的。一个连续的子数组的和可以看成当前字符串的前缀和减去某一个前缀和得到的。并且由于存在负数,前缀和并不是一直增长的。也就是说,可能存在相同的前缀和,因此我们建立一个字典存储前缀和,字典的键是前缀和,值是前缀和出现的次数。
我们只需要查询当前数列和减去target是否存在于字典中即可。
class Solution(object):
def subarraySum(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: int
"""
ans = 0
cur = 0
dic = {} # 存储前缀和出现的次数
dic[0] = 1
for num in nums:
cur += num
## 注意顺序,先判断有没有前缀和,再存入,防止读取自己
if (cur-k) in dic:
ans += dic[cur-k]
dic[cur] = dic.get(cur,0)+1
return ans
代码需要注意的细节在于,先判断有没有前缀和,再存入,防止读取自己。
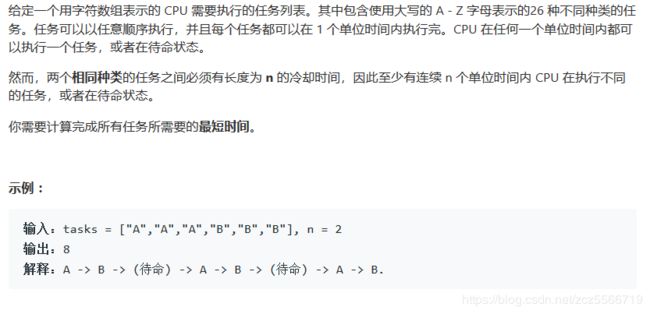
621 任务调度器
这道题目画图理解比较合适,最简单的思路是在每N+1个任务中,每次都优先安排最多的那个任务,然后依次安排其他任务。结束一次循环就对数组排序一次,更新当然最多的任务。
最后不同的任务数量小于N+1时候,补足N次。
class Solution(object):
def leastInterval(self, tasks, n):
"""
:type tasks: List[str]
:type n: int
:rtype: int
"""
# 方法1
dic = {}
ans = 0
for item in tasks:
dic[item] = dic.get(item, 0)+1
nums = list(dic.values())
nums.sort(reverse=True)
count = nums[0]
maxc = 0
for i in range(0,len(nums)):
if nums[i]-count != 0:
break
maxc += 1
return max(len(tasks), (count-1)*(n+1)+maxc)
# 方法1
right = len(nums)
while right>0:
for i in range(min(n+1,right)):
nums[i] -= 1
if nums[i] == 0:
right -= 1
ans += n+1
if right == 0:
ans -= n+1-len(nums)
nums.sort(reverse = True)
nums = nums[:right]
return ans
另外一个思路,直接计算
解释一下这个公式怎么来的 (count[25] - 1) * (n + 1) + maxCount
- 假设数组 [“A”,“A”,“A”,“B”,“B”,“C”],n = 2,A的频率最高,记为count = 3,所以两个A之间必须间隔2个任务,才能满足题意并且是最短时间(两个A的间隔大于2的总时间必然不是最短),因此执行顺序为: A->X->X->A->X->X->A,这里的X表示除了A以外其他字母,或者是待命,不用关心具体是什么,反正用来填充两个A的间隔的。上面执行顺序的规律是: 有count - 1个A,其中每个A需要搭配n个X,再加上最后一个A,所以总时间为 (count - 1) * (n + 1) + 1
- 要注意可能会出现多个频率相同且都是最高的任务,比如 [“A”,“A”,“A”,“B”,“B”,“B”,“C”,“C”],所以最后会剩下一个A和一个B,因此最后要加上频率最高的不同任务的个数 maxCount
- 公式算出的值可能会比数组的长度小,如[“A”,“A”,“B”,“B”],n = 0,此时要取数组的长度
647 回文子串
就是一道典型的回文处理题目,还是只要熟悉回文处理的模板即可。分清楚奇数和偶数分别讨论。
class Solution(object):
def countSubstrings(self, s):
num = 0
for i in range(len(s)):
num += self.ispar(i, i, s)
for i in range(len(s)-1):
num += self.ispar(i, i+1, s)
return num
def ispar(self, left, right, s):
ans = 0
while left>=0 and right<len(s):
if s[left] == s[right]:
ans += 1
left -= 1
right += 1
else:
break
return ans
739 每日温度
看到这种题目本质还是当前数字和未来的数字进行大小比较。容易想到的方法就是单调栈和优先队列。
方法一:单调栈
class Solution(object):
def dailyTemperatures(self, T):
ans = [0]*len(T)
cur = [[T[0], 0]]
for i in range(1,len(T)):
while cur and T[i] > cur[-1][0]:
value, index = cur.pop()
ans[index] = i-index
cur.append([T[i], i])
return ans
方法二:利用堆实现优先队列
class Solution:
def dailyTemperatures(self, T: List[int]) -> List[int]:
# 练习堆
heap = []
ans = [0]*len(T)
## 可以接受元组,但是第一项需要是排序项
heapq.heappush(heap, (T[0], 0))
for i in range(len(T)):
while heap and T[i]>heap[0][0]:## 足以和堆顶的第一项比较
value, index = heapq.heappop(heap)
ans[index] = i-index
heapq.heappush(heap, (T[i], i))
return ans
堆的操作还是需要熟悉,这里再复习一下:
heapq.heappush(heap, item)第一个参数是作为堆结构的数组,第二个可以是元组,但是元组的第一项是权重。- 生成一个堆的方法一个是对数组堆化,一个是先声明一个空数组再逐步往里面添加元素。
大结局
终于刷完了hot100的所有中等难度题目,心累,笔记还是得常看常复习啊!!!