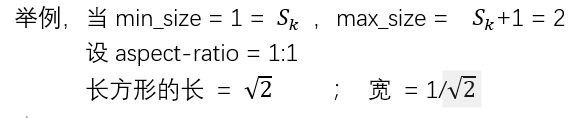目标识别—SSD网络详解

目标识别—SSD网络详解

网上的SSD解析大部分都只讲解到了Priorbox部分，最后的分类和回归并没有详细的讲解，并且论文里关于算法的一些细节也没有交代清楚。本篇文章将详细的从vgg16部分讲解到最后的识别部分。帮助大家更好的理解ssd网络，更好地进行迁移学习，以及网络优化。

论文地址：https://arxiv.org/abs/1512.02325

Ssd-caffe github ：https://github.com/weiliu89/caffe/tree/ssd

Ssd-pytorch github ：https://github.com/amdegroot/ssd.pytorch

Ssd-tensorflow github：https://github.com/balancap/SSD-Tensorflow

SSD网络算法原理：

part1：特征提取部分；

part2: priorbox选取；

part3: 分类和位置回归部分

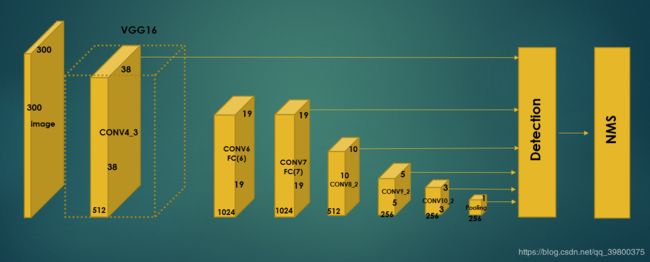
Ssd结构图：

第一部分：vgg16特征提取：

以VGG16为主的全卷积网络，用于输入图像的特征提取。SSD将VGG16最后两层FC修改成了两个卷积层(conv6，conv7)。并在之后又增加了6层卷积（conv8-1，conv8-2，conv9-1，conv9-2,conv10-1，conv10-2），最后一层使用Global Average Pool输出1x1x256的feature map。

全局平均池化就是对整个feature map 求均值，所以最后的feature map是1x1的大小。

第二部分：priorbox选取

Yolo1网络是只对最后一层的feature map 进行分类和位置回归，但ssd抽取了之前卷积层中的6层feature map 做分类和回归，最后将6层的输出concat在一起。

为什么这么做，熟悉特征提取算法的同学一定绕不开sift和surf两个经典的特征提取算法。

Sift特征提取最重要的作用之一就是实现了平移不变性和尺度不变性。

通过对原始图像高斯模糊，并构建了DOG空间。通过降采样建立了图像金字塔。

在金字塔的每层又设置不同的δ（δ为正态分布函数的标准差），得到不同尺度的高斯图像，模拟人眼对不同视野物体的实际观察效果。那么ssd同样是借鉴了这种方法。CONV4-3输出的是层级低的feature map，最后GAP输出的是层级高的feature map。

层级低的feature map模拟远而小的视野，层级高的feature map 模拟近而大的视野。

那么依据这个理论，ssd就可以识别出一张图片所有视野的物体，但实际上是这样的吗？

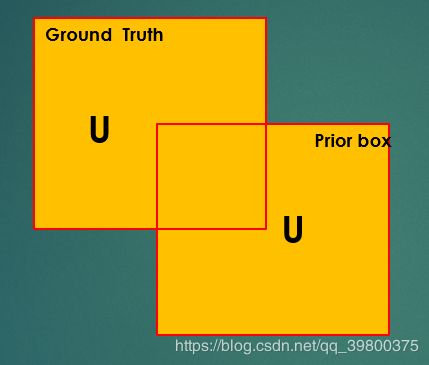
根据实际场景测试，ssd在识别小物体上仍然表现得较差，这是因为最后回归的bounding box与IoU（Intersection over Union ratio）得分有间接关系。

IoU（Intersection over Union ratio）实际上就是预测框和真实框面积的交集与并集的比值。我们认为只有IoU>0.5的priorbox才是有价值的。

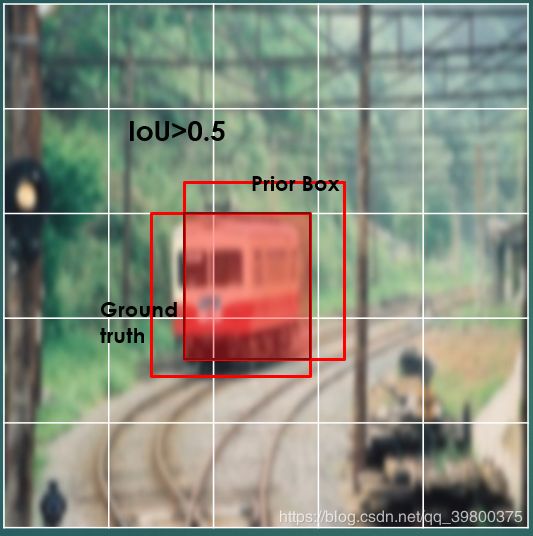
下面看一组图：
原图

卷积后

9*9feature map

5*5feature map

2*2feature map

上图中较低层级和较高层级设置的Prior box计算出的IoU得分都较低，只有中间层级设置的Prior box计算出的IoU得分较高。所以，我们保留的Prior box大多数都集中在中间层级。

细心的同学可能发现，不同尺度的feature map ，相同参数的prior box框出原图的面积不一样。这是因为层级高的feature map尺寸要比层级低的feature map尺寸小，但它们都会映射回原图，所以在prior box面积不变的情况下，小尺寸的feature map被框出了大面积，大尺寸的feature map被框出了小面积。这也就是上文提到的“层级低的feature map识别远而小的视野，层级高的feature map 识别近而大的视野。”

Prior box的选取是借鉴了faster rcnn的anchor理念，主要包括Prior box的数量和尺寸两个方面。

数量方面：以conv4_3为例，conv4_3得到的feature map 尺寸是38x38，假设该层我们设置了3种aspect-ratio的Anchor，如（1:2，1:1 2:1），那么该层的Anchor数量就是38x38x（3+1）= 5776 。为什么加+1，下面讲。

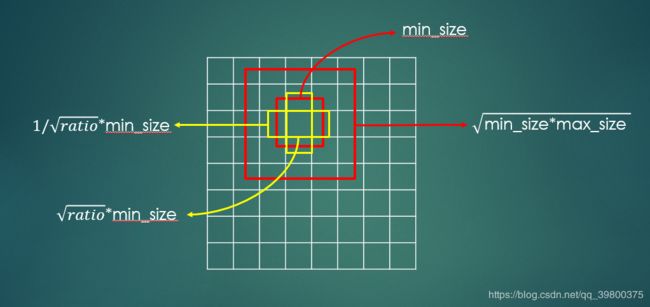
尺寸方面：同样，以conv4_3为例，

conv4_3得到的feature map每个cell中心都至少两个正方形，和若干长方形。如下图：

记小正方形的边长为min_size，大正方形的边长为

长方形的长宽分别如图。min_size和max_size由以下公式计算：

所以一个aspect-ratio对应一个矩形，上面假设该层有3种aspect-ratio，再加上边长为max_size的大正方形，那么就有38x38x（3+1）= 5776个prior_box。（与源码一致）

第三部分：预选框的处理，即类别分类和位置回归部分

很多文章对该部分的介绍很模糊而且不完整，这是因为论文原文对该部分的解释也很少。结合ssd的源码可以更加清晰地理解这一部分。

上面章节得到了6个feature map上的若干个prior box， 那么拿到这些预选框该怎么处理。

我们得到了预选框，按照正常思维，一定是要将预选框框出来的部分进行分类，并且回归出该框的具体位置（即框四个点的坐标或者原点坐标加宽高）。那么所有预选框都是良性的吗，一定不是，因为其中有大部分的都是背景或是IoU小于0.5的框，对最后的识别精度是消极的。

所以我们就需要筛掉这部分的框，只保留我们最想要的正确框。

现在就面临三个问题：1.将预选框里的内容分类；2.筛掉大部分消极框，只保留一小部分正确框。3.回归正确框的位置。

Ssd是这么做的：

还是以conv4_3为例，conv4_3得到的feature map经过L2-N（一种正则化方式，与BN有区别）和卷积，一路得到的feature map用于softmax分类，一路用于bounding box 回归。

需要注意的是，两路的feature map的shape是不同的。用于分类的feature map 的shape是[1，21xNum_priorbox，W，H]。其中21xNum_priorbox是该feature map的channels，21是类数，那么channels就等于21x5776=121296（与源码一致）。你可以这么简单理解，前21个channels包含了第一个priorbox的类别信息，即P(0-th)= 0.07，P(1-th)= 0.8，P(2-th) = 一直到P(20-th) = ，所有概率加起来等于1。以此类推，第二个priorbox，第三个priorbox……

位置回归用的是Smooth L1公式。用于位置回归的feature map的shape是[1，4xNum_priorbox，W，H]，其中4xNum_priorbox是该feature map的channels，4是因为回归位置包含了（cx,cy,w,h）四个信息。那么你也可以这么简单理解，前4个channels包含了第一个priorbox的位置信息，以此类推，第二个priorbox，第三个priorbox……

Ssd是怎么筛掉大部分消极框，只保留一小部分正确框。

分析ssd的源码可以知道，Ssd是在做完了上述两个步骤后，用NMS（非极大值抑制）来保留正确框。我个人觉得这个步骤可以放在分类和位置回归之前，先筛掉一部分IoU<阈值的框，不一定是0.5，阈值可以设置的低一些，以防误筛。这样可以减少后面位置回归和分类的计算量，这也是ssd优化的一个方向。等计算完softmax和location regression之后，再做一次NMS。

Nms的算法原理核心就是topk问题，ssd源码用的是快排。这里不过多介绍排序部分。

其中softmax的两个公式这里不过多介绍。

其中Smooth L1的公式这里不过多介绍。

其中L2-Norm的公式这里不过多介绍。

最后用数学式子表示loss函数：

C – 置信度 l – 预测框 g – 真实框。α表示两者的权重，控制两者的贡献，设为1。