支持向量机原理及求解 SVM Slater条件 KKT条件 SMO算法 软间隔
支持向量机SVM原理及求解过程介绍
支持向量机(Support Vector Machine, 简称SVM),又称为Sparse Kernel Machine或Maximum Margin Classifier,是一类经典的机器学习方法,它融合了之前已有的计算学习方法、线性判别函数和优化方法,常用于分类、回归和异常检测任务,在解决小样本问题、非线性学习和高维模式识别中有特别的优势。20世纪60年代,SVM算法的前身由俄国科学家Vapnik和Chervonenkis建立起来,到了90年代,美国科学家Corinna Cortes和Vapnik提出了基于软间隔的标准SVM算法。在深度学习兴起之前SVM有着广泛的应用和影响,至今它仍是重要的分类器和学习算法之一。本文我们将重点介绍经典SVM的求解目标和优化方法。
文章目录
- 支持向量机SVM原理及求解过程介绍
- 最大间隔超平面
- 拉格朗日乘子法,对偶问题与KKT条件
- 异常点,软间隔与核函数引入
- SMO算法求解
- SVM小结
最大间隔超平面
在机器学习中,样本经常由一系列特征来进行描述,这些特征数据构成一个向量,也构成欧式空间中的一个样本点,多个样本就可以看做欧式空间中分布的多个样本点。如果研究的是分类任务,这些样本点还经常具有类别标签信息。经典SVM研究的是二分类问题,假设现有训练集D,其中包含两类线性可分的样本,共n个:
D = ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x n , y n ) x i = ( d 1 i , d 2 i , … d m i ) T , y i = ± 1 D={(x_1,y_1 ),(x_2,y_2 ),…,(x_n,y_n)} \\ x_i=(d_{1i},d_{2i},…d_{mi} )^T,y_i=±1 D=(x1,y1),(x2,y2),…,(xn,yn)xi=(d1i,d2i,…dmi)T,yi=±1
这里 x i x_i xi表示第 i i i个样本对应的特征向量, m m m为特征维度, d j i d_{ji} dji表示样本 x i x_i xi的第 j j j个特征对应的值。 y i y_i yi表示第i个样本的标签,取值为 1 1 1或 − 1 -1 −1,分别表示正类或负类。在这 n n n个样本点分布的欧式空间中,因为样本点是线性可分的,所以可能存在多个超平面 w T x + b = 0 w^T x+b=0 wTx+b=0可以将这些点分隔开来,其中 w = ( w 1 , w 2 , … w m ) T w=(w_1,w_2,…w_m )^T w=(w1,w2,…wm)T,表示超平面的法向量,长度与样本特征维度相同为 m m m, b b b是位移项。我们所说的超平面在二维空间中是直线,在三维空间中是平面,在更高维空间中就是抽象的超平面。
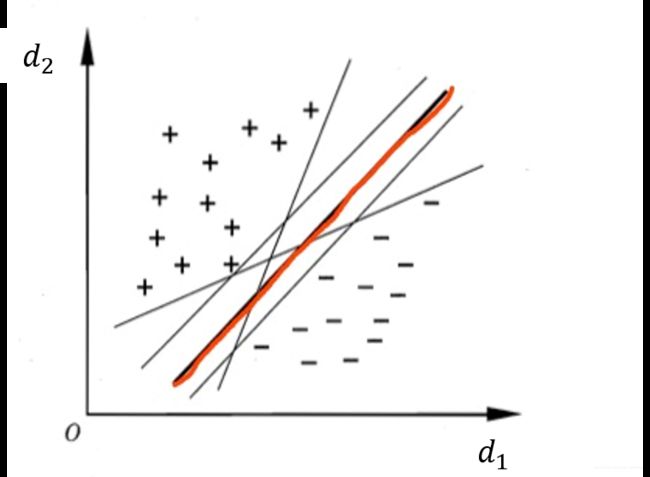
在图1中,为了简化并说明问题我们这里认为 m = 2 m=2 m=2, d 1 , d 2 d_1,d_2 d1,d2表示两个特征维度,对于任意样本点 x i x_i xi,可以根据在这两个特征维度上的值 d 1 i d_{1i} d1i, d 2 i d_{2i} d2i寻找到其在上图的二维欧式空间中对应的位置,并根据所属类别分别用 + + +或 − - −标示出来。可以看到,上图中存在多个超平面可以将这两类点分隔开来。
在二分类任务中,我们只需要找到任意一个这样的超平面,就可以成功将两类样本分开了,对于一个新样本,只需要判断它在超平面上方还是下方就可以预测其类别了。但是SVM认为随意一个超平面还不够,它希望找到一个最鲁棒最优秀的超平面,这个选择标准就是:能正确划分训练集并且几何间隔最大。所谓几何间隔最大,就是说如果从超平面两边分别选取一个距离超平面最近的点,则距离之和应该最大。SVM认为这样的超平面最鲁棒。接下来我们讲如何确定这个距离之和最大的超平面。
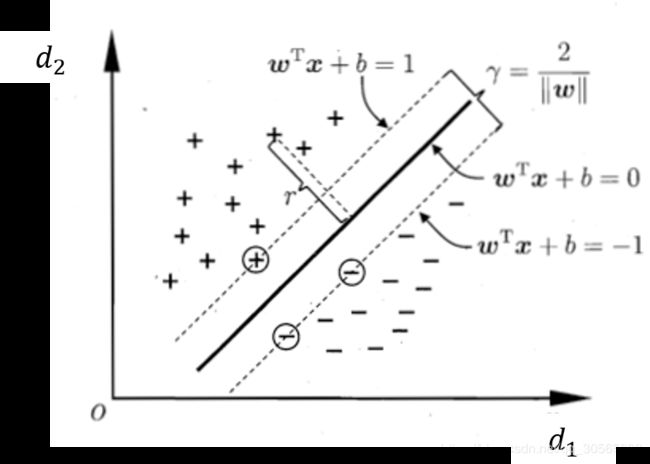
如图2所示,假设超平面上方 x x x的点均为正类即 y = + 1 y=+1 y=+1,且满足 w T x + b > 0 w^T x+b>0 wTx+b>0;超平面下方的点均为负类即 y = − 1 y=-1 y=−1,且满足 w T x + b < 0 w^T x+b<0 wTx+b<0。然后进一步加入“间隔”概念,令
f ( x ) = { ( w T x + b ≥ + 1 , i f y = + 1 w T x + b ≤ − 1 , i f y = − 1 f(x)=\left\{ \begin{aligned} (w^T x+b≥+1, & if y=+1 \\ w^T x+b≤-1, & if y=-1 \end{aligned} \right. f(x)={(wTx+b≥+1,wTx+b≤−1,ify=+1ify=−1
也就是说我们在 w T x + b = 0 w^T x+b=0 wTx+b=0这个超平面之外,还找到了对应的 w T x + b = ± 1 w^T x+b=±1 wTx+b=±1这两个超平面,两类的距离 w T x + b = 0 w^T x+b=0 wTx+b=0最近的点不可以越过 w T x + b = ± 1 w^T x+b=±1 wTx+b=±1,最次也要恰好分布在这两个超平面上。这是一个更严格的约束,我们首先假设这样的超平面是存在的。
这样的话所有的点就都满足 y ( w T x + b ) ≥ 1 y(w^T x+b)≥1 y(wTx+b)≥1。一个超平面的表达式可以有无数种,我们只选择满足以上描述的那一种就好了。恰好位于 w T x + b = ± 1 w^T x+b=±1 wTx+b=±1上的点使得等号成立,称为“支持向量”,其他的点使得大于号成立。我们知道, D D D中任何一个点到x到超平面 w T x + b = 0 w^T x+b=0 wTx+b=0的距离 r r r可以表示为:
r = ∣ w T x + b ∣ ∣ ∣ w ∣ ∣ r=\frac{|w^T x+b|}{||w||} r=∣∣w∣∣∣wTx+b∣
“ ∣ ∣ ∣ ∣ || || ∣∣∣∣”表二范数,“ ∣ ∣ | | ∣∣”表示绝对值。SVM希望 w T x + b = ± 1 w^T x+b=±1 wTx+b=±1这两个超平面之间的间隔最大,这个间隔 γ γ γ用公式表达就是:
γ = 2 ∣ ∣ w ∣ ∣ γ=\frac{2}{||w||} γ=∣∣w∣∣2
未知量是 w , b w,b w,b,求解目标是间隔 γ γ γ最大化,约束条件是 y ( w T x + b ) ≥ 1 y(w^T x+b)≥1 y(wTx+b)≥1,经典二分类SVM的优化目标用公式表达就是:
max w , b 2 ∣ ∣ w ∣ ∣ s . t . y i ( w T x i + b ) ≥ 1 , i = 1 , 2 , … n . \max\limits_{w,b} \frac{2}{||w||} \\ s.t. \quad y_i (w^T x_i+b)≥1, i=1, 2, …n. w,bmax∣∣w∣∣2s.t.yi(wTxi+b)≥1,i=1,2,…n.
拉格朗日乘子法,对偶问题与KKT条件
前面已经介绍了SVM的基本思想,下面是具体求解过程。首先我们将上述优化目标转化为等价形式:
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 s . t . y i ( w T x i + b ) ≥ 1 , i = 1 , 2 , … n . \min\limits_{w,b} \frac{1}{2} ||w||^2 \\ s.t. \quad y_i (w^T x_i+b)≥1, i=1, 2, …n. w,bmin21∣∣w∣∣2s.t.yi(wTxi+b)≥1,i=1,2,…n.
由于目标函数和约束条件都是 R n R^n Rn( n n n维实数向量空间)上连续可微的凸函数,所以这个等价形式是个凸优化问题,便于求解。凸优化问题原本有现成的计算方法和优化包可解,但是经典的SVM用的是更高效的算法。现在我们用拉格朗日乘子法建立拉格朗日函数 L ( w , b , α ) L(w, b, α) L(w,b,α),这是机器学习中的常规方法:
L ( w , b , α ) = 1 2 ∣ ∣ w ∣ ∣ 2 + ∑ i = 1 n α i ( 1 − y i ( w T x i + b ) ) s . t . y i ( w T x i + b ) ≥ 1 , i = 1 , 2 , … n . α = ( α 1 , α 2 , … , α n ) , α i ≥ 0 L(w, b, α)=\frac{1}{2} ||w||^2+\sum_{i=1}^nα_i (1-y_i (w^T x_i+b)) \\ s.t. \quad y_i (w^T x_i+b)≥1, i=1, 2, …n. \\ α=(α_1,α_2,…,α_n) , α_i≥0 L(w,b,α)=21∣∣w∣∣2+i=1∑nαi(1−yi(wTxi+b))s.t.yi(wTxi+b)≥1,i=1,2,…n.α=(α1,α2,…,αn),αi≥0
即最小化 L ( w , b , α ) L(w, b, α) L(w,b,α)。这个式子我们称为原问题。还是参数太多,难以求解。SVM使用原始问题和对偶问题做了进一步转化。我们现在假设有函数 θ ( α ) = L ( w , b , α ) θ(α)=L(w,b,α) θ(α)=L(w,b,α),以 α α α为唯一参数,以 w , b w,b w,b为常数,且 α i ≥ 0 α_i≥0 αi≥0,则 θ ( α ) θ(α) θ(α)一定是在 α i = 0 α_i=0 αi=0时取得最大值 1 2 ∣ ∣ w ∣ ∣ 2 \frac{1}{2} ||w||^2 21∣∣w∣∣2。然后再对这个最大值以 w , b w,b w,b为参数求解最小值,这样的问题就与 L ( w , b , α ) L(w, b, α) L(w,b,α)等价。也就是说,最小化 L ( w , b , α ) L(w, b, α) L(w,b,α)等价于求解下式:
min w , b max α i ≥ 0 L ( w , b , α ) \min\limits_{w,b} \max\limits_{α_i≥0}L(w, b, α) w,bminαi≥0maxL(w,b,α)
这个式子先以 α α α为参数求最大值,再以 w , b w,b w,b为参数求最小值,是一个最小最大化问题,称之为原始问题。它对应的有一个最大最小化问题,是对偶问题:
max α i ≥ 0 min w , b L ( w , b , α ) \max\limits_{α_i≥0} \min\limits_{w,b} L(w, b, α) αi≥0maxw,bminL(w,b,α)
注意原始问题是关于 w , b w,b w,b的问题,而对偶问题是关于 α α α的问题。为了方便,我们假设原始问题的最优解为 p ∗ p^* p∗,对偶问题的最优解为 d ∗ d^* d∗,即
min w , b max α i ≥ 0 L ( w , b , α ) = p ∗ max α i ≥ 0 min w , b L ( w , b , α ) = d ∗ \min\limits_{w,b} \max\limits_{α_i≥0}L(w, b, α)=p^* \\ \max\limits_{α_i≥0} \min\limits_{w,b} L(w, b, α) =d^* w,bminαi≥0maxL(w,b,α)=p∗αi≥0maxw,bminL(w,b,α)=d∗
由于
min w , b L ( w , b , α ) ≤ L ( w , b , α ) ≤ max α i ≥ 0 L ( w , b , α ) \min\limits_{w,b} L(w, b, α)≤L(w, b, α)≤\max\limits_{α_i≥0}L(w, b, α) w,bminL(w,b,α)≤L(w,b,α)≤αi≥0maxL(w,b,α)
所以
d ∗ = max α i ≥ 0 min w , b L ( w , b , α ) ≤ min w , b max α i ≥ 0 L ( w , b , α ) = p ∗ d ∗ ≤ p ∗ d^*=\max\limits_{α_i≥0} \min\limits_{w,b} L(w, b, α)≤\min\limits_{w,b} \max\limits_{α_i≥0}L(w, b, α)=p^* \\ d^*≤p^* d∗=αi≥0maxw,bminL(w,b,α)≤w,bminαi≥0maxL(w,b,α)=p∗d∗≤p∗
我们不加证明地给出以下结论:当满足Slater条件时,一定存在 ( w , b , α ) (w,b,α) (w,b,α)使得 w , b w,b w,b为原始问题的解, α α α为对偶问题的解,且 d ∗ = p ∗ = L ( w , b , α ) d^*=p^*=L(w,b,α) d∗=p∗=L(w,b,α)。Slater条件为,原问题是凸优化问题,且存在绝对可行点,所谓绝对可行点就是使得约束条件中的等式约束都成立,不等式约束都不取等号地成立的点。这样的点显然是存在的,就是那些非支持向量的点。因此对于SVM而言,我们又把问题转化成了求解原始问题和对偶问题,因为Slater条件告诉我们,把原始问题的解和对偶问题的解放在一起就是原问题的解。
为了求解,我们还需要引入KKT条件。同样不加证明地给出另一个结论: w , b w,b w,b和 α α α分别是原始问题和对偶问题的解的必要条件是w,b和α满足下面的KKT条件:
[ 1 ] L ( w , b , α ) [1] \ L(w,b,α) [1] L(w,b,α)在 w , b w,b w,b两处的偏导为0;
[ 2 ] α i ( 1 − y i ( w T x i + b ) ) = 0 , i = 1 , 2 , … , n [2]\ α_i (1-y_i (w^T x_i+b))=0 ,i=1,2,…,n [2] αi(1−yi(wTxi+b))=0,i=1,2,…,n;
[ 3 ] y i ( w T x i + b ) ≥ 1 , i = 1 , 2 , … , n [3]\ y_i (w^T x_i+b)≥1,i=1,2,…,n [3] yi(wTxi+b)≥1,i=1,2,…,n;
[ 4 ] α i ≥ 0 , i = 1 , 2 , … , n [4]\ α_i≥0,i=1,2,…,n [4] αi≥0,i=1,2,…,n;
KKT条件告诉我们怎么去求解 w , b w,b w,b和 α α α。可以看到,条件 [ 1 ] [1] [1]即原问题在最初的变量上的偏导为0,条件 [ 2 ] [2] [2]即不等式约束乘以对应的拉格朗日系数为0,条件 [ 3 ] [ 4 ] [3][4] [3][4]还是原问题的约束条件。考虑条件 [ 1 ] [1] [1],我们计算 L ( w , b , α ) L(w,b,α) L(w,b,α)在 w , b w,b w,b两处的偏导并分别令其为 0 0 0,可得到:
∑ i = 1 n α i y i x i = w ∑ i = 1 n α i y i = 0 \sum_{i=1}^nα_i y_i x_i=w \\ \sum_{i=1}^nα_i y_i=0 i=1∑nαiyixi=wi=1∑nαiyi=0
将以上两式代入 L ( w , b , α ) L(w,b,α) L(w,b,α):
L ( w , b , α ) = 1 2 ∣ ∣ w ∣ ∣ 2 + ∑ i = 1 n α i ( 1 − y i ( w T x i + b ) ) = 1 2 w T ∑ i = 1 n α i y i x i + ∑ i = 1 n α i − w T ∑ i = 1 n α i y i x i − b ∑ i = 1 n α i y i = ∑ i = 1 n α i − 1 2 w T ∑ ( i = 1 ) n α i y i x i − b ∗ 0 = ∑ i = 1 n α i − 1 2 ∑ i = 1 n α i y i x i ∑ j = 1 n α j y j x j = ∑ i = 1 n α i − 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j x i T x j L(w, b, α) =\frac{1}{2} ||w||^2+\sum_{i=1}^nα_i (1-y_i (w^T x_i+b)) \\ =\frac{1}{2} w^T \sum_{i=1}^nα_i y_i x_i+\sum_{i=1}^nα_i- w^T \sum_{i=1}^nα_i y_i x_i-b \sum_{i=1}^nα_i y_i \\ =\sum_{i=1}^nα_i- \frac{1}{2} w^T \sum_(i=1)^nα_i y_i x_i-b*0 \\ =\sum_{i=1}^nα_i- \frac{1}{2} \sum_{i=1}^nα_i y_i x_i \sum_{j=1}^nα_j y_j x_j \\ =\sum_{i=1}^nα_i- \frac{1}{2} \sum_{i=1}^n\sum_{j=1}^nα_i α_j y_i y_j x_i^T x_j L(w,b,α)=21∣∣w∣∣2+i=1∑nαi(1−yi(wTxi+b))=21wTi=1∑nαiyixi+i=1∑nαi−wTi=1∑nαiyixi−bi=1∑nαiyi=i=1∑nαi−21wT(∑i=1)nαiyixi−b∗0=i=1∑nαi−21i=1∑nαiyixij=1∑nαjyjxj=i=1∑nαi−21i=1∑nj=1∑nαiαjyiyjxiTxj
这就是我们现在经过对偶问题转化后的求解目标:
max α ∑ i = 1 n α i − 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j x i T x j s . t . α i ≥ 0 ; ∑ i = 1 n α i y i = 0 \max\limits_α \sum_{i=1}^nα_i- \frac{1}{2} \sum_{i=1}^n\sum_{j=1}^nα_i α_j y_i y_j x_i^T x_j \\ s.t. \quad α_i≥0;\sum_{i=1}^nα_i y_i =0 αmaxi=1∑nαi−21i=1∑nj=1∑nαiαjyiyjxiTxjs.t.αi≥0;i=1∑nαiyi=0
可以看到这个式子中唯一的变量是 α α α, w , b w,b w,b已经被约去了,有利于求解。而 w w w与 α α α的关系为 ∑ i = 1 n α i y i x i = w \sum_{i=1}^nα_i y_i x_i=w ∑i=1nαiyixi=w, b b b与 α α α的关系为的关系为 α i ( 1 − y i ( w T x i + b ) ) = 0 α_i (1-y_i (w^T x_i+b))=0 αi(1−yi(wTxi+b))=0,前面均已给出。在 b b b与 α α α的关系中,需要注意, α i α_i αi的值不可能都为 0 0 0,如果都为 0 0 0的话根据 ∑ i = 1 n α i y i x i = w \sum_{i=1}^nα_i y_i x_i=w ∑i=1nαiyixi=w, w w w也就恒为 0 0 0了,这显然是不可能的。当 α i α_i αi不为 0 0 0,对应的 1 − y i ( w T x i + b ) 1-y_i (w^T x_i+b) 1−yi(wTxi+b)就必定为 0 0 0,对应的那些点就是支持向量。也就是说,超平面的表达式仅仅与支持向量有关,这与我们从图上得到的直观感受是一致的。
异常点,软间隔与核函数引入
我们前面一直假设这些样本点是线性可分的,即一定存在超平面可以将两类样本点分隔开,然而事实上这样的超平面有时并不存在,如下图:

我们当然不希望一颗老鼠屎坏了一锅汤,因此引入“软间隔”的概念,允许一些错误样本存在。我们引入松弛变量 ξ ξ ξ:
min w , b , ξ 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 n ξ i s . t . y i ( w T x i + b ) ≥ 1 − ξ i ξ i ≥ 0 , i = 1 , 2 , … n \min\limits_{w,b,ξ} \frac{1}{2}||w||^2+C\sum_{i=1}^nξ_i \\ s.t. \quad y_i (w^T x_i+b)≥1- ξ_i \\ ξ_i ≥0 , i=1, 2, …n w,b,ξmin21∣∣w∣∣2+Ci=1∑nξis.t.yi(wTxi+b)≥1−ξiξi≥0,i=1,2,…n
只需要满足 y i ( w T x i + b ) + ξ i ≥ 1 y_i (w^T x_i+b)+ξ_i≥1 yi(wTxi+b)+ξi≥1即可,这时异常点就可以通过对应一个正值的 ξ i ξ_i ξi来衡量它到自己类别一侧的距离,正常点对应的 ξ i ξ_i ξi就为0。优化目标中也加入了 ∑ i = 1 n ξ i \sum_{i=1}^nξ_i ∑i=1nξi , C C C是一个可调节的参数, C C C较大时对错误分类的乘法较大,较小时对错误分类的惩罚较小。如前所述,对这个式子使用拉格朗日乘子法:
L ( w , b , ξ , α , μ ) = 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 n ξ i + ∑ i = 1 n α i ( 1 − ξ i − y i ( w T x i + b ) ) − ∑ i = 1 n μ i ξ i s . t . y i ( w T x i + b ) ≥ 1 − ξ i i = 1 , 2 , … , n α i ≥ 0 , μ i ≥ 0 , ξ i ≥ 0 L(w, b,ξ,α,μ)=\frac{1}{2} ||w||^2+C\sum_{i=1}^nξ_i +\sum_{i=1}^nα_i (1-ξ_i-y_i (w^T x_i+b))-\sum_{i=1}^nμ_i ξ_i \\ s.t. \quad y_i (w^T x_i+b)≥1- ξ_i i=1,2,…,n \\ α_i≥0,μ_i≥0,ξ_i≥0 L(w,b,ξ,α,μ)=21∣∣w∣∣2+Ci=1∑nξi+i=1∑nαi(1−ξi−yi(wTxi+b))−i=1∑nμiξis.t.yi(wTxi+b)≥1−ξii=1,2,…,nαi≥0,μi≥0,ξi≥0
新的 L ( w , b , ξ , α , μ ) L(w, b,ξ,α,μ) L(w,b,ξ,α,μ)同样满足Slater条件。然后应用KKT条件求解对应的原始问题和对偶问题:
[ 1 ] L ( w , b , ξ , α , μ ) [1]\ L(w, b,ξ,α,μ) [1] L(w,b,ξ,α,μ)在 w , b , ξ w, b,ξ w,b,ξ三处的偏导均为 0 0 0;
[ 2 ] [2] [2] α i ( 1 − ξ i − y i ( w T x i + b ) ) = 0 , i = 1 , 2 , … , n α_i (1-ξ_i-y_i (w^T x_i+b))=0,i=1,2,…,n αi(1−ξi−yi(wTxi+b))=0,i=1,2,…,n;
[ 3 ] [3] [3] μ i ξ i = 0 , i = 1 , 2 , … , n μ_i ξ_i=0 ,i=1,2,…,n μiξi=0,i=1,2,…,n;
[ 4 ] [4] [4] y i ( W T x i + b ) + ξ i − 1 ≥ 0 , i = 1 , 2 , … , n y_i (W^T x_i+b)+ξ_i-1≥0 ,i=1,2,…,n yi(WTxi+b)+ξi−1≥0,i=1,2,…,n;
[ 5 ] [5] [5] α i ≥ 0 , μ i ≥ 0 , ξ i ≥ 0 , i = 1 , 2 , … , n α_i≥0, μ_i ≥0,ξ_i≥0,i=1,2,…,n αi≥0,μi≥0,ξi≥0,i=1,2,…,n;
还是和前面类似,条件 [ 1 ] [1] [1]是原问题在最初的变量 w , b , ξ w, b,ξ w,b,ξ上的偏导为 0 0 0,条件 [ 2 ] [ 3 ] [2][3] [2][3]即不等式约束乘以对应的拉格朗日系数为 0 0 0,条件 [ 4 ] [ 5 ] [4][5] [4][5]还是原问题和拉格朗日乘子法的约束。现在我们把三个偏导为 0 0 0计算出来可以得到:
∑ i = 1 n α i y i x i = w ∑ i = 1 n α i y i = 0 C = α i + μ i \sum_{i=1}^nα_i y_i x_i =w \\ \sum_{i=1}^n α_i y_i =0 \\ C= α_i+μ_i i=1∑nαiyixi=wi=1∑nαiyi=0C=αi+μi
再把三式代入 L ( w , b , ξ , α , μ ) L(w, b,ξ,α,μ) L(w,b,ξ,α,μ),其实得到的结果和前一部分得到的结果一样,只是改变了 α i α_i αi的取值范围(因为 C = α i + μ i C=α_i+μ_i C=αi+μi且 μ i ≥ 0 μ_i ≥0 μi≥0,所以 0 ≤ α i ≤ C 0≤α_i≤C 0≤αi≤C),这里就不展开了,直接给出结果:
max α ∑ i = 1 n α i − 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j x i T x j s . t . 0 ≤ α i ≤ C ∑ i = 1 n α i y i = 0 \max_α \sum_{i=1}^nα_i- \frac{1}{2} \sum_{i=1}^n\sum_{j=1}^nα_i α_j y_i y_j x_i^T x_j \\ s.t.\quad 0≤α_i≤C \\ \sum_{i=1}^nα_i y_i =0 αmaxi=1∑nαi−21i=1∑nj=1∑nαiαjyiyjxiTxjs.t.0≤αi≤Ci=1∑nαiyi=0
这个式子仍然仅以 α α α为变量, α α α与 w , b , ξ w,b,ξ w,b,ξ的关系都由KKT条件给出了。到这里还没完,我们介绍的软间隔是为了优化线性不可分问题,软间隔只是优化这个问题的很多种方法之一,在SVM中还有一种常见的方法就是引入核函数(或称为核方法),这里一并介绍。
核函数的功能是通变换或映射,将在当前空间中线性不可分的样本点映射到新的空间中,使得样本点在新空间中变得线性可分。在SVM中,假设有一个映射 ϕ ( x ) ϕ(x) ϕ(x),使得输入样本分布的欧式空间 X X X中的超曲面模型对应于一个特征空间 H Η H中的超平面模型,这样,分类任务就可以通过在特征空间中求解线性的支持向量机来完成。核函数 K ( x , z ) K(x,z) K(x,z)是对于所有 x , z ∈ X x,z∈X x,z∈X都满足条件
K ( x , z ) = ϕ ( x ) ⋅ ϕ ( z ) K(x,z)=ϕ(x)·ϕ(z) K(x,z)=ϕ(x)⋅ϕ(z)
的函数。其中 ϕ ( x ) ϕ(x) ϕ(x)是映射函数, K ( x , z ) K(x,z) K(x,z)是核函数, ϕ ( x ) ⋅ ϕ ( z ) ϕ(x)·ϕ(z) ϕ(x)⋅ϕ(z)是 ϕ ( x ) ϕ(x) ϕ(x)和 ϕ ( z ) ϕ(z) ϕ(z)的内积。在机器学习中,经常只定义核函数 K ( x , z ) K(x,z) K(x,z),而不显式地定义映射函数 ϕ ( x ) ϕ(x) ϕ(x),直接计算 K ( x , z ) K(x,z) K(x,z)比较容易,计算 ϕ ( x ) ⋅ ϕ ( z ) ϕ(x)·ϕ(z) ϕ(x)⋅ϕ(z)却不容易,而且 H Η H一般是高维的甚至是无穷维的。
回到前面得到的求解目标,我们用核函数 K ( x i , x j ) K(x_i,x_j ) K(xi,xj)代替其中的 x i T x j x_i^T x_j xiTxj,将样本点映射到线性可分的空间中:
max α ∑ i = 1 n α i − 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j K ( x i , x j ) s . t . 0 ≤ α i ≤ C ∑ i = 1 n α i y i = 0 \max_α \sum_{i=1}^nα_i- \frac{1}{2} \sum_{i=1}^n\sum_{j=1}^nα_i α_j y_i y_j K(x_i,x_j ) \\ s.t.\quad 0≤α_i≤C \\ \sum_{i=1}^nα_i y_i=0 αmaxi=1∑nαi−21i=1∑nj=1∑nαiαjyiyjK(xi,xj)s.t.0≤αi≤Ci=1∑nαiyi=0
这就是我们最终的优化目标了。
SMO算法求解
我们在前一部分得到了加入软间隔和核函数的SVM的优化目标,这也就是最常见的SVM了。即使约去了 w , b , ξ w,b,ξ w,b,ξ,这个优化目标仍然难以求解,因为 α α α是一个长度为 n n n的向量, D D D中样本数量越多求解就越复杂。虽然是个凸优化,但是用求导、偏导为0这样的方法仍然比较难解决,复杂度太高。这里介绍一种序列最小最优化(Sequential Minimal Optimization,SMO)算法,是常见的解决这一优化目标的方法。
α = ( α 1 , α 2 , . . . , α n ) , α i ≥ 0 α=(α_1,α_2,...,α_n) , α_i≥0 α=(α1,α2,...,αn),αi≥0
SMO算法是一种启发式算法,它的基本思路是:如果所有变量的解都满足此最优化问题的KKT条件,那么这个最优化问题的解就得到了。SMO重复以下步骤直到收敛:从 α α α中选取两个待更新的变量 α i , α j α_i,α_j αi,αj,固定其他值,构建一个二次规划的子问题;求解子问题,获得更新后的 α i , α j α_i,α_j αi,αj。因为这个子问题是可以通过解析方法求解的,所以大大提高了算法计算效率。子问题的两个变量,一个变量选违反KKT条件最严重的一个,另一个是可变化幅度最大的。这样SMO算法就不断将问题分解为对子问题的求解。
为了不失一般性,假设我们现在选取了两个变量 α 1 , α 2 α_1,α_2 α1,α2,其他变量 α 3 , … , α n α_3,…,α_n α3,…,αn都是固定的。根据约束条件 ∑ i = 1 n α i y i = 0 \sum_{i=1}^nα_i y_i=0 ∑i=1nαiyi=0可知, α 1 y 1 + α 2 y 2 α_1 y_1+α_2 y_2 α1y1+α2y2的值其实也是固定的。我们假设 α 1 , α 2 α_1,α_2 α1,α2原本的值为 α 1 o l d , α 2 o l d α_1^old,α_2^old α1old,α2old,更新后的值为 α 1 n e w , α 2 n e w α_1^new,α_2^new α1new,α2new,则有:
α 1 n e w y 1 + α 2 n e w y 2 = α 1 o l d y 1 + α 2 o l d y 2 = − ∑ i = 3 n α i y i = ς α_1^{new}y_1+α_2^{new} y_2=α_1^{old} y_1+α_2^{old} y_2=-\sum_{i=3}^nα_i y_i=ς α1newy1+α2newy2=α1oldy1+α2oldy2=−i=3∑nαiyi=ς
ς ς ς是一个常数。原优化目标可以写为:
min α ∑ i = 1 n α i − 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j K ( x i , x j ) s . t . 0 ≤ α i ≤ C ∑ i = 1 n α i y i = 0 \min_α \sum_{i=1}^nα_i- \frac{1}{2} \sum_{i=1}^n\sum_{j=1}^nα_i α_j y_i y_j K(x_i,x_j ) \\ s.t.\quad 0≤α_i≤C \\ \sum_{i=1}^nα_i y_i=0 αmini=1∑nαi−21i=1∑nj=1∑nαiαjyiyjK(xi,xj)s.t.0≤αi≤Ci=1∑nαiyi=0
我们去掉优化目标中与 α 1 α_1 α1, α 2 α_2 α2无关的项可得到:
min α 1 , α 2 1 2 K 11 α 1 2 + 1 2 K 22 α 2 2 + K 12 α 1 α 2 y 1 y 2 + α 1 y 1 ∑ 3 n α i y i K i 1 + α 2 y 2 ∑ 3 n α i y i K i 2 − ( α 1 + α 2 ) s . t . α 1 y 1 + α 2 y 2 = ς , 0 ≤ α 1 , α 2 ≤ C \min_{α_1,α_2} \frac{1}{2} K_{11} α_1^2+\frac{1}{2} K_{22} α_2^2+K_{12} α_1α_2y_1 y_2+α_1 y_1 \sum_{3}^{n}α_i y_i K_{i1}+α_2y_2 \sum_{3}^{n}α_i y_i K_{i2}-(α_1+α_2 ) \\ s.t.\quad α_1 y_1+α_2 y_2=ς, 0≤α_1,α_2≤C α1,α2min21K11α12+21K22α22+K12α1α2y1y2+α1y13∑nαiyiKi1+α2y23∑nαiyiKi2−(α1+α2)s.t.α1y1+α2y2=ς,0≤α1,α2≤C
其中 K i j K_{ij} Kij表示 K ( x i , x j ) K(x_i,x_j ) K(xi,xj)。然后用 α 2 α_2 α2表示 α 1 α_1 α1:
α 1 y 1 + α 2 y 2 = ς α 1 y 1 y 1 + α 2 y 2 y 1 = ς y 1 = α 1 + α 2 y 1 y 2 α 1 = y 1 ( ς − α 2 y 2 ) α_1 y_1+α_2 y_2=ς \\ α_1 y_1 y_1+α_2 y_2 y_1=ςy_1=α_1 +α_2 y_1 y_2 \\ α_1 = y_1 (ς-α_2 y_2 ) α1y1+α2y2=ςα1y1y1+α2y2y1=ςy1=α1+α2y1y2α1=y1(ς−α2y2)
然后再把 α 1 α_1 α1也约去,只留下 α 2 α_2 α2:
min α 2 1 2 K 11 ( ς − α 2 y 2 ) 2 + 1 / 2 K 22 α 2 2 + K 12 ( ς − α 2 y 2 ) α 2 y 2 + ( ς − α 2 y 2 ) v 1 + α 2 y 2 v 2 − α 2 − y 1 ( ς − α 2 y 2 ) \min_{α_2} \frac{1}{2} K_{11} (ς-α_2 y_2)^2+1/2 K_{22} α_2^ 2+K_{12} (ς-α_2 y_2 ) α_2 y_2+(ς-α_2 y_2 ) v_1+α_2 y_2 v_2-α_2 -y_1 (ς-α_2 y_2 ) α2min21K11(ς−α2y2)2+1/2K22α22+K12(ς−α2y2)α2y2+(ς−α2y2)v1+α2y2v2−α2−y1(ς−α2y2)
其中:
v 1 = ∑ 3 n α i y i K 1 i v 2 = ∑ 3 n α i y i K 2 i v_1=\sum_3^nα_i y_i K_{1i} \\ v_2=\sum_3^nα_i y_i K_{2i} v1=3∑nαiyiK1iv2=3∑nαiyiK2i
上式对 α 2 α_2 α2 求导并令导数为 0 0 0得:
α 2 ( K 11 + K 22 − 2 K 12 ) = y 2 ( y 2 − y 1 + ς K 11 − ς K 12 + v 1 − v 2 ) = y 2 ( y 2 − y 1 + ς K 11 − ς K 12 + ( g ( x 1 ) − ∑ 1 2 α i y i K 1 i − b ) − ( g ( x 2 ) − ∑ 1 2 α i y i K 2 i − b ) g ( x ) = ∑ 1 n α i y i K ( x , x i ) + b α_2 (K_{11}+K_{22}-2K_{12} )=y_2 (y_2-y_1+ςK_{11}-ςK_{12}+v_1-v_2) \\ =y_2 (y_2-y_1+ςK_{11}-ςK_{12}+(g(x_1 )-\sum_1^2α_i y_i K_{1i}-b)-(g(x_2 )-\sum_1^2α_i y_i K_{2i}-b) \\ g(x)=\sum_1^nα_i y_i K(x,x_i )+b α2(K11+K22−2K12)=y2(y2−y1+ςK11−ςK12+v1−v2)=y2(y2−y1+ςK11−ςK12+(g(x1)−1∑2αiyiK1i−b)−(g(x2)−1∑2αiyiK2i−b)g(x)=1∑nαiyiK(x,xi)+b
那么再将 α 1 o l d y 1 + α 2 o l d y 2 = − ∑ i = 3 n α i y i = ς α_1^{old} y_1+α_2^{old} y_2=-\sum_{i=3}^nα_i y_i=ς α1oldy1+α2oldy2=−∑i=3nαiyi=ς代进来,得到:
α 2 n e w , u n c ( K 11 + K 22 − 2 K 12 ) = y 2 ( ( K 11 + K 22 − 2 K 12 ) α 2 o l d y 2 + y 2 − y 1 + g ( x 1 ) − g ( x 2 ) ) = ( K 11 + K 22 − 2 K 12 ) α 2 o l d + y 2 ( E 1 − E 1 ) E i = g ( x i ) − y i α_2^{new,unc} (K_{11}+K_{22}-2K_{12} )=y_2 ((K_{11}+K_{22}-2K_{12} ) α_2^ {old} y_2+y_2-y_1+g(x_1 )-g(x_2 )) \\ =(K_{11}+K_{22}-2K_{12} ) α_2^ {old}+y_2 (E_1-E_1) \\ E_i=g(x_i )-y_i α2new,unc(K11+K22−2K12)=y2((K11+K22−2K12)α2oldy2+y2−y1+g(x1)−g(x2))=(K11+K22−2K12)α2old+y2(E1−E1)Ei=g(xi)−yi
这里就可以得到:
α 2 n e w , u n c = α 2 o l d + y 2 ( E 1 − E 2 ) K 11 + K 22 − 2 K 12 α_2^{new,unc}=α_2^{ old}+\frac{y_2 (E_1-E_2) }{K_{11}+K_{22}-2K_{12} } α2new,unc=α2old+K11+K22−2K12y2(E1−E2)
这个得到的新的 α 2 n e w α_2^{new} α2new还需要再根据取值范围再做调整,因此标记为"new,unc(lliped)"。这里可能有读者会疑惑为什么一会儿是 α 2 n e w α_2^{ new} α2new一会儿是 α 2 o l d α_2^ {old} α2old,解释一下,前面已经得到了唯一的关于 α 2 α_2 α2 的式子,这个式子的解就是 α 2 n e w , u n c α_2^{new,unc} α2new,unc,但是我们在解的过程中引入了 g ( x ) g(x) g(x),通过 g ( x ) g(x) g(x)引入的就是 α 2 o l d α_2^{ old} α2old。
因为约束条件比较多,解出来的结果 α 2 n e w , u n c α_2^{new,unc} α2new,unc未必满足约束,所以我们考虑一下 α 2 α_2 α2 的取值范围。假设 L ≤ α 2 ≤ H L≤α_2≤H L≤α2≤H, L , H L,H L,H需要计算。
首先至少 0 ≤ α 1 , α 2 ≤ C 0≤α_1,α_2≤C 0≤α1,α2≤C必须满足。前面已经得到 α 1 y 1 + α 2 y 2 = ς α_1 y_1+α_2 y_2=ς α1y1+α2y2=ς,注意 y 1 , y 2 y_1,y_2 y1,y2的值要么是 + 1 +1 +1要么是 − 1 -1 −1。考虑两种情况:
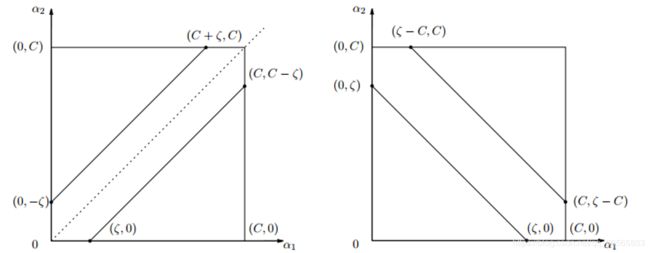
[ 1 ] [1] [1] 若 y 1 ! = y 2 , α 1 − α 2 = ς y_1!=y_2, α_1-α_2=ς y1!=y2,α1−α2=ς,即可画出图4的左侧图,上下两条斜线分别对应 ς ς ς为负和为正的情况,此时 L = m a x ( 0 , − ς ) , H = m i n ( C , C − ς ) L=max(0,-ς),H=min(C,C-ς) L=max(0,−ς),H=min(C,C−ς)
[ 2 ] [2] [2] 若 y 1 = y 2 , α 1 + α 2 = ς y_1=y_2 , α_1+α_2=ς y1=y2,α1+α2=ς,即可画出图4的右侧图,上下两条斜线分别对应 ς ς ς大于 C C C和小于 C C C的情况,此时 L = m a x ( 0 , ς − C ) , H = m i n ( C , ς ) L=max(0,ς-C),H=min(C,ς) L=max(0,ς−C),H=min(C,ς)
这样我们就得到了 L , H L,H L,H的值。
根据得到的取值范围我们再调整前面算出的 α 2 n e w , u n c α_2^{new,unc} α2new,unc,得到 α 2 n e w , c l i p p e d α_2^{new,clipped} α2new,clipped:
α 2 n e w , c l i p p e d = { H , i f α 2 n e w , u n c > H α 2 n e w , u n c , i f L ≤ α 2 n e w , u n c ≤ H L , i f α 2 n e w , u n c < L α_2^{new,clipped}=\left\{ \begin{aligned} &H, & if α_2^{new,unc}>H \\ &α_2^{new,unc}, & if L≤ α_2^{new,unc}≤H \\ &L, & if α_2^{new,unc} < L \end{aligned} \right. α2new,clipped=⎩⎪⎨⎪⎧H,α2new,unc,L,ifα2new,unc>HifL≤α2new,unc≤Hifα2new,unc<L
这样就解决了 α 2 α_2 α2的更新问题,进而解决了 α 1 α_1 α1的更新。
我们还需要介绍 α 1 α_1 α1和 α 2 α_2 α2的选择方法。前面说SMO算法每次选取两个变量时,一个变量选择违反KKT条件最严重的,另一个变量是可变化幅度最大的。这里再细化一下具体怎样操作。
首先是怎样选取第一个变量 α 1 α_1 α1,这个选取过程是SMO算法的外层循环。顺序是,首先遍历所有 0 < α i < C 0<α_i
然后是怎样选取第二个变量 α 2 α_2 α2,标准是希望 α 2 α_2 α2有足够大的变化。前面已经计算出,变化幅度依赖于 ∣ E 1 − E 2 ∣ |E_1-E_2 | ∣E1−E2∣, α 1 α_1 α1确定后 E 1 E_1 E1就确定下来了,如果 E 1 E_1 E1为正就选择最小的 E i E_i Ei为 E 2 E_2 E2,如果 E 1 E_1 E1为负就选最大的 E i E_i Ei为 E 2 E_2 E2。为了加快速度,所有的 E i E_i Ei都被保存在一个列表中供随时查取。
在每次选取并更新完 α 1 , α 2 α_1,α_2 α1,α2后,都需要重新计算 b b b。由KKT条件 w = ∑ i = 1 n α i y i x i w=\sum_{i=1}^nα_i y_i x_i w=∑i=1nαiyixi,加入核函数并代入 y = w T x + b y=w^T x+b y=wTx+b可知:
∑ 1 n α i y i K ( x , x i ) + b = y \sum_1^nα_i y_i K(x,x_i )+b=y 1∑nαiyiK(x,xi)+b=y
则有:
b 1 n e w = y 1 − ∑ 3 n α i y i K 1 i − α 1 n e w y 1 K 11 − α 2 n e w y 2 K 12 b_1^{new}=y_1-\sum_3^nα_i y_i K_{1i}-α_1^ {new} y_1 K_{11}-α_2^ {new} y_2 K_{12} b1new=y1−3∑nαiyiK1i−α1newy1K11−α2newy2K12
由于 E i = g ( x i ) − y i = ∑ 1 n α i y i K ( x , x i ) + b − y i E_i=g(x_i )-y_i= \sum_1^nα_i y_i K(x,x_i )+b-y_i Ei=g(xi)−yi=∑1nαiyiK(x,xi)+b−yi,得:
y 1 − ∑ 3 n α i y i K 1 i = − E i + α 1 o l d y 1 K 11 + α 2 o l d y 2 K 12 + b 1 o l d y_1-\sum_3^nα_i y_i K_{1i}=-E_i+α_1^ {old} y_1 K_{11}+α_2^ {old} y_2 K_{12}+b_1^{old} y1−3∑nαiyiK1i=−Ei+α1oldy1K11+α2oldy2K12+b1old
也就是说:
b 1 = b − E 1 − y 1 ( α 1 n e w − α 1 o l d ) K 11 − y 2 ( α 2 n e w − α 2 o l d ) K 12 b 2 = b − E 2 − y 1 ( α 1 n e w − α 1 o l d ) K 11 − y 2 ( α 2 n e w − α 2 o l d ) K 12 b_1=b-E_1-y_1 (α_1^ {new}-α_1^ {old} ) K_{11}-y_2 (α_2^{ new}-α_2^ {old} ) K_{12} \\ b_2=b-E_2-y_1 (α_1^{ new}-α_1^ {old} ) K_{11}-y_2 (α_2^ {new}-α_2^ {old} ) K_{12} b1=b−E1−y1(α1new−α1old)K11−y2(α2new−α2old)K12b2=b−E2−y1(α1new−α1old)K11−y2(α2new−α2old)K12
一般的更新原则是:
b = { b 1 , i f 0 < α 1 n e w < C b 2 , i f 0 < α 2 n e w < C b 1 + b 2 2 , o t h e r w i s e b=\left\{ \begin{aligned} &b_1, & if 0<α_1^{new}
SVM小结
到这里我们就完成了SVM的介绍,这部分做个总结。
支持向量机SVM的核心思想就是寻找超平面分开不同类的点,并使得支持向量到超平面的距离最大化,超平面仅与支持向量有关。最简单的情况是线性可分支持向量机,条件是数据线性可分。为了处理非线性分布的数据,我们介绍了软间隔概念并引入核函数。在求解过程中,我们首先使用拉格朗日乘子法得到拉格朗日函数这个原问题,又证明了它与所谓的原始问题等价,满足Slatter条件表明原始问题与对应的的对偶问题和原问题的最值存在且相等,并且把前两者的解放在一起就是原问题的解。利用KKT条件我们得到了 w , b w,b w,b与 α α α的关系,简化了计算。SMO算法通过迭代地选择最不符合KKT条件的点和变化幅度最大的点,以及更新b值,加快了运算速度,解决了问题。
经典SVM仅面向二分类问题,要解决多分类问题需要构建多个SVM来完成,而且经典SVM不能给出分类准确率。SVM算法复杂度较高,在大规模样本量上难以快速训练。它的主要优点是,对异常点不敏感,增删非支持向量对模型无影响,在小样本数据上表现良好。