数学建模（五）：图与网络模型

&1.概论
历史上第一篇图论论文，是欧拉提出著名的“哥尼斯堡七桥问题”，那个图就是这样的：
图论中的图，实际上表达的是某些指定事物以及它们之间的联系。比如“七桥问题问题中”，四个点代表的就是普莱格尔河的两个岛以及河的两岸。我们先通过一些例子来感受一下网络优化问题。
例1 最短路问题（SPP-shortest path problem)
一名货柜车司机奉命在最短的时间内将一车货物从甲地运往乙地。从甲地到乙地的公路网纵横交错，因此有多种行车路线，这名司机应选择哪条线路呢?假设货柜车的运行速度是恒定的，那么这一问题相当于需要找到一条从甲地到乙地的最短路。
例2 公路连接问题
某地区有若干个主要城市，先准备修建高速公路把这些城市连接起来，使得从其中任何一个城市都可以经高速公路直接或间接到达另一个城市。假定已经知道了任意两个城市之间修建高速公路的成本，那么应如何决定在哪些城市间修建高速公路，使得总成本最小?
例3 指派问题（assignment problem）
一家公司经理准备安排N名员工去完成N项任务，每人一项。由于各员工的特点不同，不同的员工去完成同一项任务时所获得的回报是不同的。如何分配工作方案可以使总回报最大?
例4 中国邮递员问题(CPP-chinese postman problem)
一名邮递员负责投递某个街区的邮件。如何为他(她)设计一条最短的投递路线(从 邮局出发，经过投递区内每条街道至少一次，最后返回邮局)?由于这一问题是我国管梅谷教授 1960 年首先提出的，所以国际上称之为中国邮递员问题。
例5的旅行商问题（TSP-traveling salesman problem）和例6的运输问题（transportation problem）略去。我们可以看到这些问题实际上都可以归于最优化问题，同时这些问题的模型都可以用图与网络的形式直观表达，与图和网络相关的最优化问题，我们称为网络最优化问题。多数的网络最优化问题都是以流（flow）作为研究对象，因此这样的问题又被称为网络流或者是网络流规划等。
下面首先介绍图与网络的一些基本概念。
&2.图与网络的基本概念
1）无向图
⎡顶点集⎦或「节点集」（vertex set or node set）：由平面上所有的点作为元素组成的集合，这些点称为「顶点」或「节点」。
用数学形式表达，即V(G)={v₁,v₂,…,v_n}，V(G)为顶点，v_i为顶点或节点。
「边集」（edge set）：连接顶点与顶点之间的边作为元素组成的集合。数学形式上的表达为E(G)={e₁,e₂,…,e_m}，其中的e_i世界上是V(G)中的两个不同元素的无序对，可以写作e_i=v_jv_k=v_kv_j=(v_j,v_k)=(v_kv_j)，称为这个图从v_j到v_k的一条边。
「无向图」（undirected graph）：是由V(G)和E(G)组合起来的二元组，记作G=(V(G),E(G))。
「相邻」（adjacent）：当e_k=v_iv_j时，我们称v_i,v_j是e_k的端点，并且这两个点相邻；边e_k称为和它的两个端点关联（incident）。如果说两条边在图G中相邻，那么这两条边在图G至少有一个公共端点。
「赋权无向图」或「无向网络」（undirected network）：在边上赋予权值的无向图被称为赋权无向图或无向网络。
「有限图」：指顶点集和边集都是有限集合的图。图G的顶点数用符号|V|或者是(G)表示，边数用|E|或(G)表示。
「环」（loop）：端点重合为一点的边。
「简单图」（simple graph）：既没有环也没有两条边同时连接统一对顶点的图称为简单图。
2）有向图
「弧集」（arc set）：连接图中顶点的有向边称为弧，数学形式表达，若V(G)为点集，A(G)={a₁,a₂,…,a_n}中，a_i=(v_j,v_k)=v_jv_k，是v_j与v_k的有序对，a_i被称为从v_j到v_k的一条弧。
当弧a_i=v_jv_k，称v_j为尾，v_k为头，这个是比较反常的一点，但没办法，就是这么规定的。同时a_i是v_j的出弧，是v_k的入弧。
3）完全图、二分图
「完全图」：每一对不同的顶点都有一条边相邻的简单图称为完全图，n个顶点的完全图称为K_n。
若V(G)=XUY,X∩Y=∅,|X||Y|≠0，X中无相邻点对，Y中也是，则称这样的图为二分图（bipartite graph）；特别地，若∀x∈X,∀y∈Y，都有v_xv_y∈E(G)，称G为完全二分图，记为K_|X|,|Y|。
4）子图（gubgraph）
当V(H)⊂V(G),E(H)⊂E(G)；图H就称为图G的子图，G是H的母图。G的支撑子图（spanning subgraph，又称为生成子图）指满足V(H)=V(G)的子图。
5）度（degree）
对于V(G)中的v，G中与v关联的边数（环算作两条边）称为v的度，记作d(v)。若d(v_i)为奇数，则称v_i为奇数点（odd point），若d(v_i)为偶数则称v_i为偶数点。关于顶点的度，我们有如下结果：
(i)一个图中所有点的度数之和是边数的两倍；
(ii)任意一个图的奇顶点的个数是偶数；
6） 图与网络的数据结构
介绍五种在计算机上能够描述图与网络的数据结构：邻接矩阵、关联矩阵、弧表、邻接表、星形表，以下介绍都是假设在G=(V,A)是一个简单有向图的前提下进行的。
(i)邻接矩阵表示法
邻接矩阵（adjacency matrix）定义如下：假如网络中有n个点，那么邻接矩阵C是一个n*n的0-1矩阵，有C=(c_ij)_n*n∈{0,1}^n*n,当a_ij存在于A中时，矩阵元素c_ij取1，否则取0；
举例如下：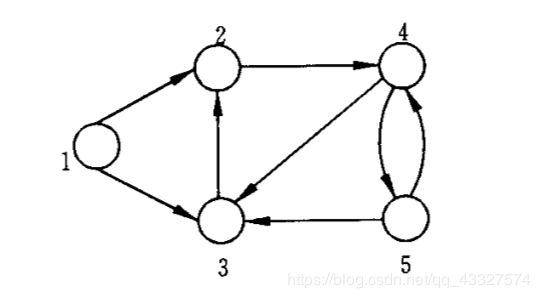

使用邻接矩阵表示上述有向图，可以得到

c=[0 1 1 0 0
   0 0 0 1 0
   0 1 0 0 0
   0 0 1 0 1
   0 0 1 1 0]

假如网络中的边有权值，那就可以将邻接矩阵中的1替换为相应的权值，这样赋权有向图也可以用邻接矩阵进行表示。
(ii)关联矩阵表示法
关联矩阵在图G=(V,A)中的表示如下：B是一个n*m的矩阵，即
B=(b_ik)_n*m∈{-1,0,1}^n*m，当v_i是图中的某一个点，k代表着网络中所有弧组成的集合的顺序，也就是说关联矩阵表达的是图上某一点与图上的某一条弧的关系，如果该点为该弧的起点，则b_ik=1，如果该点为该弧的终点，则b_ik=-1，如果该点与该弧没有关联，则b_ik=0；
对于邻接矩阵中给出的有向图，我们把弧(1,2),(1,3),(2,4),(3,2),(4,3),(4,5),(5,3),(5,4),那么关联矩阵表示为

[1   1  0  0  0  0  0  0
 -1  0  1 -1  0  0  0  0
 0  -1  0  1 -1  0  -1 0
 0   0 -1  0  1  1  0 -1
 0.  0. 0. 0. 0 -1  1  1 ]

如果要通过关联矩阵表达一个赋权有向图，那么可以新增一行来储存弧的权值。
(iii)弧表表示法
弧表表示法非常的简单，直接一个例子就能懂，还是讲述邻接矩阵时用的有向图，我们给它每条弧加上一个权值，有

我们可以使用字典来储存弧表。
(iv)邻接表表示法
我们用指针数组表示邻接表，数组的每个元素都是链表形式，链表中每个单元都作为一道出弧，同时将权值作为数据域，比如弧表中的赋权有向图，我们可以表示为：

(v)星形表示法
星形表示法由两个数组组成，一个是节点对应的出弧的起始地址的编号，另一个是记录弧信息的数组。第一个数组被我们称作point，它的元素个数比顶点数多1，且point(1)=1，point(n+1)=m+1，这种叫做前向星形表示法，用这种方法表示上面的例子，有：

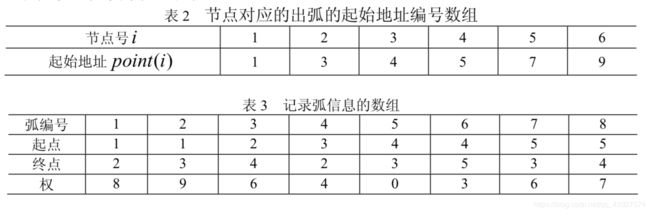
而反向星形则是为了说明入弧，于是有：
我们可以看到，前向星形和反向星形中，同一条弧的编号不同，我们可以使用一个trace数组来记录这种对应关系，即

7）路与连通
对于W=v₀e₁v₁e₂…e_kv_k，称W是图G一条道路，v_I∈V(G),e_I∈E(G)，如果道路中的边互不相同，则W称为迹；若道路中W顶点互不相同，W称为路。
如果一条道路是闭路，那么它的起点和终点相同，起点和终点重合的轨称为圈；如果两个顶点u,v之间存在道路，那么称u和v连通(connected)，它们之间的最短路的长称为u,v之间的距离，即d(u,v)。假若图G的任意两个顶点均联通，则称G是连通图。有以下两个推论：
(i)图P是一条轨的充要条件是P是连通的，且有两个度为1的顶点，其余顶点的度为2；
(ii)图C是一个圈的充要条件是C是各顶点的度为2的连通图。

&3.最短路问题
1)Dijkstra算法
给定一个链接了若干个城镇的铁路网络，在这个网络的两个指定城镇间，找一条最短铁路线。我们将每一个城镇作为顶点，每一条赋权的边作为连接两个城镇的铁路，我们可以得到一个赋权无向图。这样问题就转化成了两个顶点u₀,v₀之间具有最小权的路。这条路叫作最短路，这些权值之和称为u₀到v₀的距离，记作d(u₀,v₀)。
求最短路已有成熟的算法：Dijkstra算法。基本思想为按照从u₀的从近到远为顺序，依次求出所有顶点到u₀的最短距离。下面我们给出该算法的详细过程：
(i)令l(u₀)=0,l(v_i)=∞（除u₀外），S₀={u₀}，i=0。
(ii)对每个v∈S_i’(S_i’=V\S_i)有l(v_i)=min{l(v_i),l(u_i)+w(uv)}，将达到最小值的顶点记为u_i+1，令S_i+1=S_i∪{u_i+1}。
(iii)若i=|V|-1，停止；若i<|V|-1，则i+=1，转(ii)。
例9 某公司在六个城市c₁,c₂,…,c₆有分公司，从c_i到c_j的直接航程票价记在下面的矩阵(i,j)位置上（若为∞表示无直接航路），请帮助公司设计从c₁到其他城市的票价最便宜的路线图。
关于matlab使用Dijkstra算法解决该问题的代码书中已经给出，我在这里给出一种python实现的方法：

from math import *

a = []
a.append([0,50,inf,40,25,10])
a.append([50,0,15,20,inf,25])
a.append([inf,15,0,10,20,inf])
a.append([40,20,10,0,10,25])
a.append([25 ,inf, 20, 10, 0 ,55])
a.append([10, 25, inf, 25, 55, 0])

def find(visited,temp):
    visited_ = visited.copy()
    while 1 in visited_:
        id1 = visited_.index(1)
        temp[id1] = inf
        visited_[id1] = 0
    return temp

def find_2(visited):
    id2 = []
    visited_ = visited.copy()
    while 0 in visited_:
        id2.append(visited_.index(0))
        visited_[visited_.index(0)]=1
    return id2

def dijkstra(mat,start,end):
    path = [end]
    n = len(mat)
    visited = [0 for i in range(n)]
    distance = [inf for i in range(n)]
    distance[start] = 0
    parent = [0 for i in range(n)]
    for i in range(n-1):
        temp = distance.copy()
        temp = find(visited,temp)
        t = min(temp)
        u = temp.index(t)
        visited[u] = 1
        id2 = find_2(visited)
        for j in id2:
            if distance[j] >= t + mat[u][j]:
                distance[j] = t + mat[u][j]
                parent[j] = u
            else:pass
    if parent[end] != start:
        t = parent[end]
        while t != start:
            path.append(t)
            t = parent[t]
        path.append(t)
    path.reverse()
    return distance[end],path

if __name__ =="__main__":
    print(dijkstra(a,0,1))

关于局部变量与全局变量，以及将变量赋给另一个变量和将变量的拷贝赋给另一个变量的区别，是编程方面的问题，我在调试过程中深感自己编程基础的薄弱。这段代码我没有进行注释，假如您有任何不解之处，可以询问我。
（4.28待更新）
2）Floyd算法
Floyd算法的基本思想是：递推产生一个矩阵序列A₀,A₁,…,A_k,…,A_n，其中A_k(i,j)表示从顶点v_i到v_j的路径上所经过的顶点序号不大于k的最短路径长度。在计算时我们使用迭代公式：
A_k(i,j)=min(A_k-1(i,j),A_k-1(i,k)+A_k-1(k,j))，k为迭代次数，i,j,k=1,2,…,n。
这里我给出一种实现的python代码，要注意到Floyd方法的时间复杂度为O(n³)，
对于时间复杂度，我写了一篇博文进行浅显的解释：数据结构与算法（一）：用时间复杂度评价算法

从中我们可以看到，Floyd的算法复杂度是灾难级别的。在一些对时间复杂度要求较高的地方应谨慎使用，但我们这里的算法主要为建模服务，所以无需考虑这么多。

def floyd(mat,start,end):
    n = len(mat)
    for i in range(n):
        for j in range(n):
            for k in range(n):
                if mat[j][k] > mat[j][i] + mat[i][k]:mat[j][k] = mat[j][i] + mat[i][k]
    return mat[start][end]

&4.树
连通的无圈图叫做树，记作T。图G有V(G)=V(T)，E(T)⊂E(G)，称T是G的生成树。图G连通的充要条件是G有生成树。一个连通图的生成树的个数很多，用（G）表示G的生成树个数，有(G)=(G-e)+(G·e)，G-e表示从G上删除边e，G·e表示把e的长度收缩为零得到的图。
树的五个充要条件：(i)G是树当且仅当G中任意两个顶点之间有且仅有一条道路；
(ii)G是树当且仅当G无圈，且=v-1;
(iii)G是树当且仅当G连通，且=v-1;
(iv)G是树当且仅当G连通，且∀e∈E(G)，G-e不连通；
(v)G是树当且仅当G连通，且∀e∉E(G)，G+e有且仅有一个圈；

假设我们要修筑n个城市的铁路使得这些城市连通起来，同时每个城市到另一个城市的铁路修建都需要花费一定的建造费用，我们需要获得在连通赋权图上求权最小的最小生成树
1）prim算法构造最小生成树
设置两个集合P和Q，P用于存放G的最小生成树中的顶点，集合Q存放G的最小生成树中的边。令集合P的初值为P={v₁}（假设构造最小生成树时，从顶点v₁出发），集合Q中的初值为Q=∅，prim算法的思想是，从所有p∈P，v∈V-P的边中，选取具有最小权值的边pv，将顶点v加入集合P中，将边pv加入集合Q中，如此不断重复，知道P=V时，此时集合Q中包含了最小生成树的所有边。
prim算法如下：
(i)P={v₁},Q=∅;
(ii)while P ~= V
找最小边pv，其中p∈P，v∈V-P，
P=P+{v}，Q=Q+{pv}
我们给出如下的网络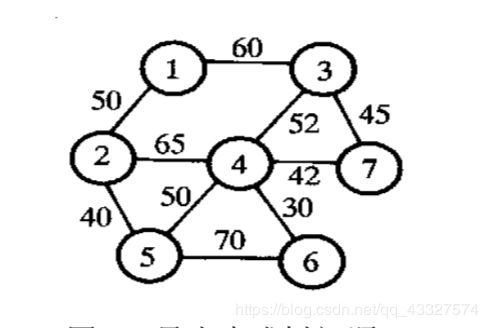
要求求出网络中的最小生成树问题，这里我给出一种使用python实现的prim算法求解的代码：

from math import *

a = []
a.append([0,50,60,inf,inf,inf,inf])
a.append([50,0,inf,65,40,inf,inf])
a.append([60,inf,0,52,inf,inf,45])
a.append([inf,65,52,0,50,30,42])
a.append([inf ,40, inf, 50, 0 ,70,inf])
a.append([inf, inf, inf, 30, 70, 0,inf])
a.append([inf,inf,45,42,inf,inf,0])

def prim(mat,start):
    price = 0
    P = [start]
    Q = []
    V = [i for i in range(len(mat))]
    V_P = V.copy()
    V_P.pop(start)
    while len(P) != len(V):
        edges = []
        weights = []
        for i in P:
            for j in V_P:
                edges.append([i,j])
                weights.append(mat[i][j])
        min_edge = min(weights)
        price = price + min_edge
        P.append(edges[weights.index(min_edge)][1])
        V_P.remove(edges[weights.index(min_edge)][1])
        Q.append(edges[weights.index(min_edge)])
    return price,Q
print(prim(a,0))

不难看出，prim算法的时间复杂度是灾难级别的，因此我们再讲述一种Kruskal方法，如下：
(i)选取e₁∈E(G)，使得w(e₁)=min；
(ii)若选取完毕e₁,e₂,…,e_i，那么从E(G)-{e₁,e₂,…,e_i}中选取e_i+1满足w(e_i+1)=min，同时G[{e₁,e₂,…,e_i+1}]中无圈；
(iii)直到选得e_v-1为止；