SVM算法

1.SVM作用：

（1）分类

（2）回归

 

2. 不适定性问题

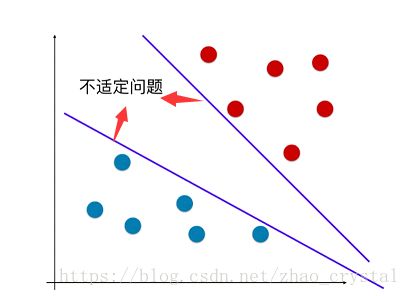
2.1 什么是不适定性问题

分类就是通过决策边界来将不同的数据分开，如下图的二分类问题，在决策边界（蓝色直线）右侧的为一类，在决策边界左侧的为一类。可以看到决策边界是不唯一的，这就是我们通常所说的不适定性问题。

 

2.2 怎样解决不是定性问题？

逻辑回归算法解决不适定性问题：定义概率函数（sigmod函数），建模使cost函数最小-----得到最佳的决策边界。

SVM算法解决不是定性问题：完全由训练数据集决定。

 

3. SVM 算法解决不适定性问题的具体过程

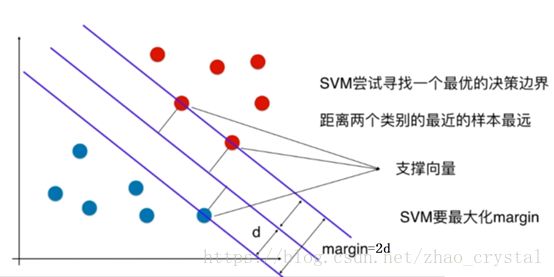
3.1 Hard-margin SVM

（1）什么是hard-margin SVM

 

 

SVM要最大化margin，即：使d最大，d为距离决策边界最近的点到决策边界的距离。

补充知识：点到直线的距离（高维空间中为点到平面的距离）

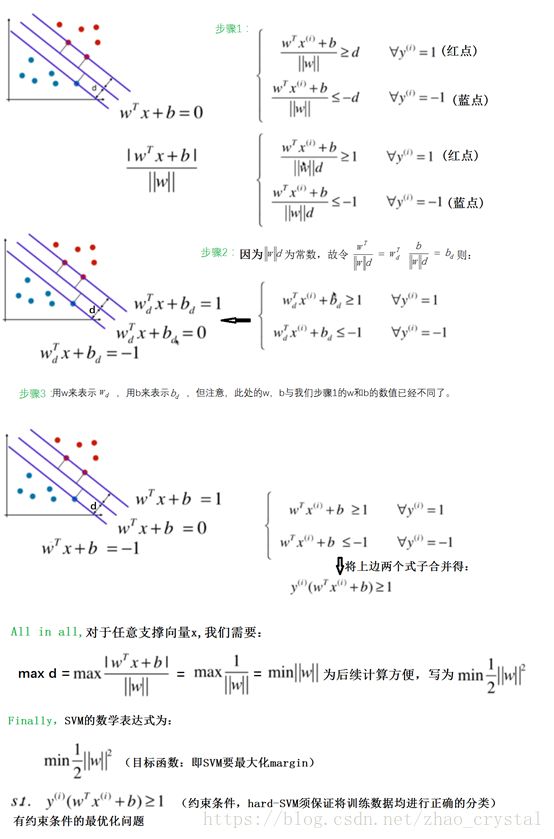
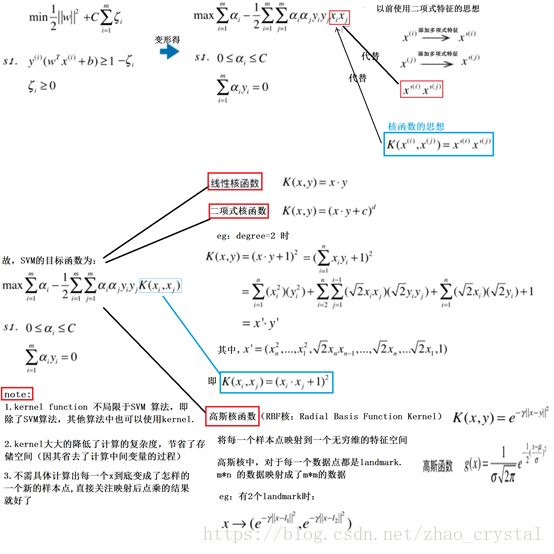
（2）hard-margin SVM 目标函数及约束条件的推导过程

 

3.2 Soft-margin SVM

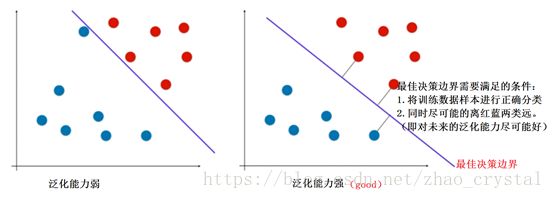
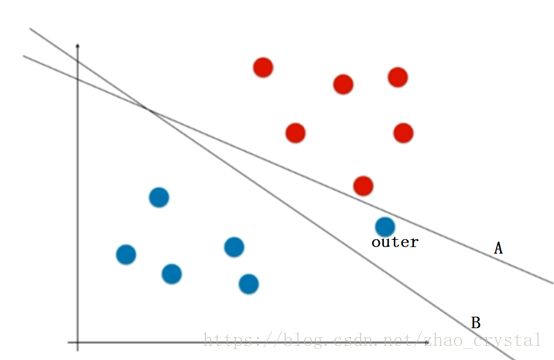
（1）Soft-SVM的决策边界VS Hard-SVM的决策边界

 

上图中，有两条决策边界A,B；

决策边界A（对应于hard-SVM）将训练数据完全正确的进行了分类，但是泛化能力很弱（红点和蓝点距离决策边界都很近，当进来的新的数据点在决策边界附件时，很容易被分错）

决策边界B（对应于Soft-SVM）虽然把训练数据集中的一个蓝点归到了红点那一类，但是具有较强的泛化能力。（因为决策边界B距离蓝红点的距离都比较远）实际中，我们主要关注的是对新来的（即我们要预测的）数据的预测能力，因此，往往我们会选择决策边界B。

另外，点“outer”可能是一个极度特殊的点；也有可能是我们数据的标签错误。

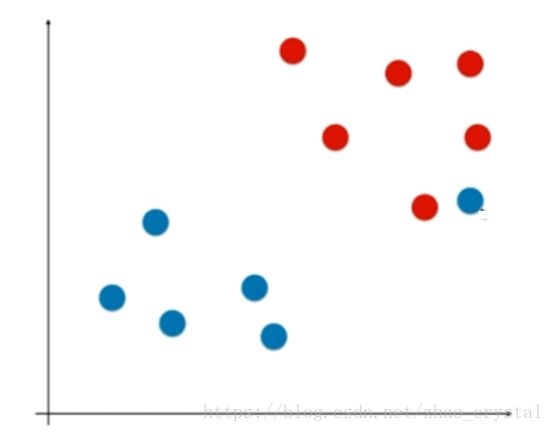
(2) 数据线性不可分，非Soft-SVM莫属

更糟糕的：在二维空间中，有时不能用一条直线将训练数据进行完全正确的分类，即数据是线性不可分的（如下图所示），此时只能用Soft-SVM。

 

(3)soft-margin-SVM的具体计算过程

 

(4)SVM 中的L1正则与L2正则。

 

类比二项式回归的目标函数，我们也可把目标函数中的第二部分看作正则项，同正则化的原理相同，都是让模型对一些特殊的点不那么敏感，有一定的容错能力，增强泛化效果。

但注意：和的形式相同，但意义却不同， ： margin的宽松距离，而是特征前边的权重。

C的位置也可以加在第一项的前边，但含义是一样的。

在这里，C越大，容错越小。

 

4. 用sklearn 中的 LinearSVC来对线性可分的数据进行分类

（1） 载入鸢尾花数据集中的前两类的前两个特征（即为了可视化，处理简单的有两个特征的二分类问题）

（2）首先，和KNN一样，涉及到距离，要做数据的标准化处理

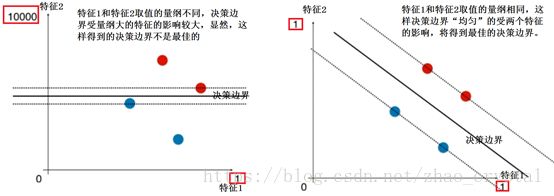
如下图所示，特征1和特征2的数值不在一个量级上，这样划分出来的决策边界就可能会受量级较高的特征的影响较大。

 

具体地，在程序中：

from sklearn.preprocessing import StandardScaler

from sklearn.svm import LinearSVC（SVC： support vector classifier）

note参数：

• penalty：string, ‘l1’ or ‘l2’ (default=’l2’)（即表示L1正则和L2正则）
•  C : float, optional (default=1.0)，Penalty parameter C of the error term（即正则化项前的系数）C越大，越偏向于hard-margin SVM，C越小，越偏向于soft-margin SVM .

（3）绘制决策边界

利用LinearSVC的Attributes: coef_ 和 intercept_ 来绘制margin.

Note:

• coef_ 指的是特征前面的系数，即权重；程序中输出的 coef_ 是一个二维的数组，因为sklearn中的 svm 算法是可以直接解决多分类问题的，如果是三分类问题，则coef_ 中就包含两个数组，分别代表两条决策边界的系数。
• Intercept_ 指的是截距。

具体程序见：sklearn_SVM_plot_decision_boundary.ipynb

 

5. 使用SVM算法，对决策边界不是线性的数据进行分类

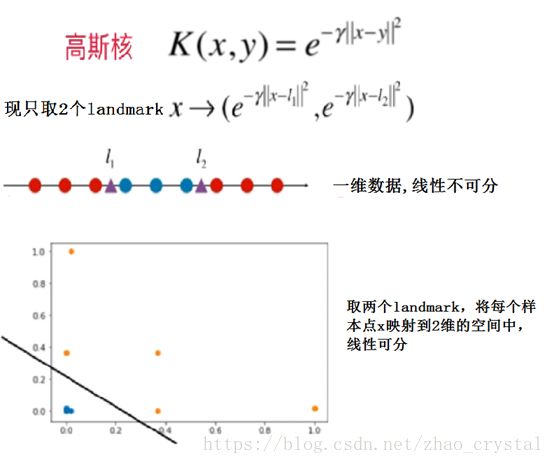
5.1分类原理：

 

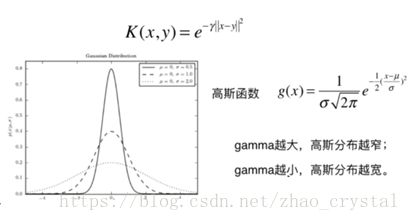
高斯核函数与高斯函数的关系：

 

5.2举两个简单的例子，对以上原理进行实际操作，可视化结果

 

 

具体程序见：RBFKernel.ipynb

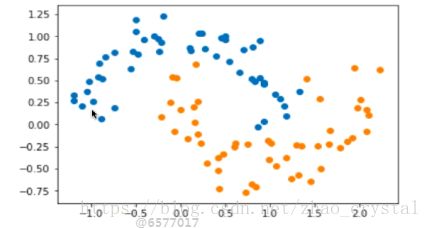
5.3 用不同的方法对make_moons（决策边界是非线性的）数据集进行分类

数据集如下图所示

 

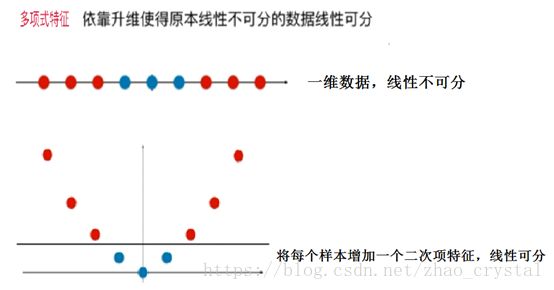
 (1)用以前线性回归解决非线性数据的思想，给每个样本加入多项式特征。

即用polynormal的方式先对数据转换成高维的，使得样本有多项式项的特征，然后再用LinearSVC对样本进行分类。

def polylinearSVC(degree, C)

    return Pipline([(“poly”, PolynomialFeature(degree=2)),

                    ( “std_Scaler”, StandardScaler()),
                    (“linearSVC”, LinearSVC (C = C))

         ])

(2) 多项式核: SVM算法可直接使用多项式的特征      

def polynomialkernelSVC(degree, C)

    return Pipline([(

                    ( “std_Scaler”, StandardScaler()),

                    (“SVC”, SVC (kernel = “poly”, degree = degree, C=C))

         ])

 

(3)高斯核：

def RbfkernelSVC(gamma, C)

    return Pipline([(
          ( “std_Scaler”, StandardScaler()),
          (“SVC”, SVC ( gamma = gamma,C=C))

         ])

Note: SVC中参数kernel 默认的为 “rbf”

从程序的运行结果来看，gamma越大，训练的模型会过拟合；gamma越小，训练的模型会欠拟合。

具体程序见：polySVM_kernelPolysvm.ipybb

                     sklearn_svm_gamma.ipynb

6. 用SVM思路解决回归问题

 

6.1 用LinearSVR, 或SVR 回归波士顿房价

From sklearn.svm import LinearSVR, SVR

SVR: support vector regression

具体程序见：linearSVR_SVR.ipynb

 

注意两对对应函数：

	分类	回归
解决线性问题	LinearSVC	LinearSVR
解决非线性问题	SVC	SVR

当然：在样本加上多项式特征时，也可用LinearSVC和LinearSVR 来解决非线性问题。