poj1966 Network（最小割）

题意

给定一张无向图，求去掉多少个点，可以使图不连通。

题解

最小割
去掉一个点的代价为1，随便枚举两个点，就有了S和T，求最小割掉几个点使S和T不连通？
看似很最小割模板，但是最小割割的是边啊！所以我们要进行点边转换。
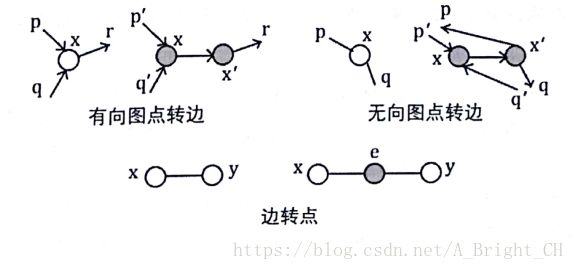
借用lyd一张图：

把每个点拆成入点x和出点x’，先连一条(x,x',1)。
对于原图中(x,y)，按“出点连入点”的原则，(x',y,inf),(y',x,inf)。
在此基础上跑最小割就大功告成了。
实现时为了再提一下速，我们可以把S点定为1或1'，T点再去枚举。

代码

#include
#include
#include
#define id(i,j) i+j*n
using namespace std;
const int inf=(1<<30)-1;
const int maxn=60;

int n,m;

inline int read()
{
    int re=0;char ch=getchar();
    while(ch<'0' || ch>'9') ch=getchar();
    while(ch>='0' && ch<='9') re=re*10+(ch^48),ch=getchar();
    return re;
}

bool ma[maxn][maxn];
struct E{int y,c,next;}e[(maxn*maxn+maxn)*2];int len,last[maxn*2];//debug 大小 
void ins(int x,int y,int c)
{
    e[++len]=(E){y,c,last[x]};last[x]=len;
    e[++len]=(E){x,0,last[y]};last[y]=len;
}

int S,T;
void make_edge()
{
    len=1;memset(last,0,sizeof(last));
    for(int i=1;i<=n;i++)
        if(i!=S && i!=T) ins(id(i,0),id(i,1),1);
        else ins(id(i,0),id(i,1),inf);
    for(int x=1;x<=n;x++)
        for(int y=1;y<=n;y++)
            if(ma[x][y]) ins(id(x,1),id(y,0),inf);
}

int h[maxn*2];
int head,tail,q[maxn*2];
bool bfs()
{
    head=0,tail=1;q[0]=S;
    memset(h,0,sizeof(h));h[S]=1;
    while(head0;
}

int dinic(int x,int flow)
{
    if(x==T) return flow;
    int rest=flow;
    for(int k=last[x];k;k=e[k].next)
    {
        int y=e[k].y;
        if(e[k].c && h[y]==h[x]+1)
        {
            int incf=dinic(y,min(rest,e[k].c));
            rest-=incf;
            e[k].c-=incf;e[k^1].c+=incf;
            if(rest==0) break;
        }
    }
    if(rest==flow) h[x]=0;
    return flow-rest;
}

int main()
{
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        if(n==0){puts("0");continue;}
        if(n==1){puts("1");continue;}
        memset(ma,false,sizeof(ma));
        for(int i=1;i<=m;i++)
        {
            int x=read()+1,y=read()+1;
            ma[x][y]=ma[y][x]=true;
        }
        int ans=n;
        for(int i=1;i<=2;i++)//1->1，2->1'
            for(int j=1;j<=n;j++) if(i!=j)
            {
                S=i,T=id(j,0);//注意T是某个点的入点
                make_edge();
                int tans=0,flow;
                while(bfs())
                    while(flow=dinic(S,inf)) tans+=flow;
                ans=min(ans,tans);
            }
        printf("%d\n",ans);
    }
    return 0;
}