AI之路（三）——关于统计学习（statistical learning）Part 2 分类

上篇博文中叙述了统计学习或机器学习的定义、研究对象与学习方法，本篇叙述统计学习的分类。
统计学习的基本分类是监督学习、无监督学习、强化学习。

统计学习或机器学习是一个范围宽阔、内容繁多、应用广泛的领域，并不存在（至少现在不存在）一个统一的理论体系涵盖所有内容。下面从几个角度对统计学习方法进行分类。

基本分类

统计学习或机器学习一般包括监督学习、无监督学习、强化学习。有时还包括半监督学习、主动学习。
1.监督学习
监督学习（supervised learning）是指从标注数据中学习预测模型的机器学习问题。标注数据表示输入输出的对应关系，预测模型对给定的输入产生相应的输出。监督学习的本质是学习输入到输出的映射的统计规律。
（1）输入空间、特征空间和输出空间
在监督学习中，将输入与输出所有可能取值的集合分别称为输入空间（input space）与输出空间（output space）。输入与输出空间可以是有限元素的集合，也可以是整个欧式空间。输入空间与输出空间可以是同一个空间，也可以是不同的空间；但通常输出空间远远小于输入空间。
每个具体的输入是一个实例（instance），通常由特征向量（feature vector）表示。这时，所有特征向量存在的空间称为特征空间（feature space）。特征空间的每一维对应于一个特征。有时假设输入空间与特征空间为相同的空间，对它们不予区分；有时假设输入空间与特征空间为不同的空间，将实例从输入空间映射到特征空间。模型实际上都是定义在特征空间上的。
在监督学习中，将输入与输出看作是定义在输入（特征）空间与输出空间上的随机变量的取值。
输入输出变量用大写字母表示，习惯上输入变量写作$X$，输出变量写作$Y$。输入输出变量的取值用小写字母表示，输入变量的取值写作$x$，输出变量的取值写作$y$。变量可以是标量或向量，都用相同类型字母表示。
输入实例$x$的特征向量记作
$$x=(x^{(1)},x^{(2)},\dots ,x^{(i)},\dots ,x^{(n)}{)}^T$$
$x^{(i)}$表示$x$的第$i$个特征。注意：$x^{(i)}$与$x_i$不同，通常用$x_i$表示多个输入变量中的第$i$个变量，即
$$x_i=(x_i^{(1)},x_i^{(2)},\dots ,x_i^{(i)},\dots ,x_i^{(n)}{)}^T$$
监督学习从训练数据（training data)集合中学习模型，对测试数据（test data）进行预测。训练数据由输入（或特征向量）与输出对组成，训练集通常表示为
$$T=\{((x_1,y_1),(x_2,y_2),\dots \dots ,(x_n,y_n))\}$$
测试数据也由输入与输出对组成，输入与输出对又称为样本（sample）或样本点。
输入变量$X$和输出变量$Y$有不同的类型，可以是连续的，也可以是离散的。人们根据输入输出变量的不同类型，对预测任务基于不同的名称：输入变量与输出变冷了均为连续变量的预测问题称为回归问题；输出变量为有限个离散变量的预测问题称为分类问题；输入变量与输出变量均为变量序列的预测问题称为标注问题。
随机变量序列：一般的，如果用 $(x_1,x_2,\dots \dots ,x_n)$代表随机变量，这些随机变量如果按照顺序出现，就形成了随机序列，记做 $(x_n)$。**这种随机序列具备两种关键的特点：其一，序列中的每个变量都是随机的；其二，序列本身就是随机的。随机变量序列是统计学和概率论中的重要概念，详细可参考百度百科中关于随机序列的描述随机序列：

（2）联合概率分布
监督学习假设输入与输出的随机变量$X$和$Y$遵循联合概率分布$P(X,Y)$。$P(X,Y)$表示分布函数，或分布密度函数。注意在学习过程中，假定这一联合概率分布存在，但对学习系统来说，联合概率分布的具体定义是未知的。训练数据与测试数据被看作是依联合概率分布$P(X,Y)$独立同分布产生的。统计学习假设数据存在一定的统计规律，$X$和$Y$具有联合概率分布就是监督学习关于数据的基本假设。
（3）假设空间
监督学习的目的在于学习一个由输入到输出的映射，这一映射由模型来表示。换句话说，学习的目的就在于找到最好的这样的模型。模型属于由输入空间到输出空间的映射的集合，这个集合就是假设空间（hypothesis space）。假设空间的确定意味着学习的范围的确定。
监督学习的模型可以是概率模型或非概率模型，由条件概率分布$P(Y|X)$或决策函数（decision function）$Y=f(X)$表示，随具体学习方法而定。对具体的输入进行相应的输出预测时，写作$P(y|x)$或$y=f(x)$。

（4）问题的形式化
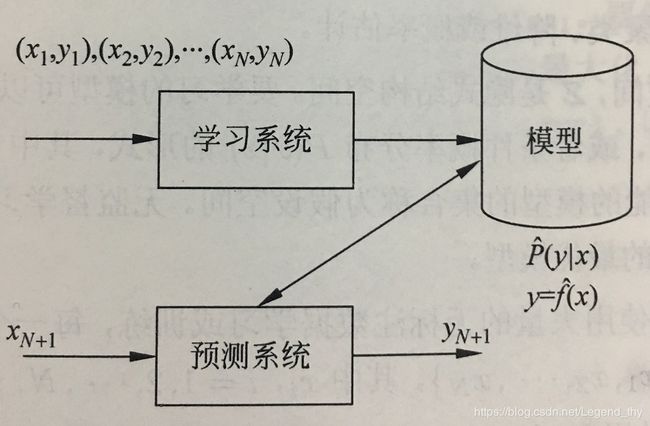
监督学习利用训练数据集学习一个模型，再用模型对测试样本集进行预测。由于在这个过程中需要标注的训练数据集，而标注的训练数据集往往都是人工给出的，所以称为监督学习。监督学习分为学习和预测两个过程，由学习系统与预测系统完成，可用下图来描述。

首先给定一个训练数据集
$$T=\{((x_1,y_1),(x_2,y_2),\dots \dots ,(x_n,y_n))\}$$
其中$(x_i,y_i),i=1,2,\dots ,N$,称为样本或样本点。$x_i\in \chi \subseteq {\mathrm{R}}^{\mathrm{n}}$是输入的观测值，也称为输入或实例，$y_i\in \mathrm{y}$是输出的观测值，也称为输出。
监督学习分为学习和预测两个过程，由学习系统与预测系统完成。在学习过程中，学习系统利用给定的训练数据集，通过学习（或训练）得到一个模型，表示为条件概率分布$\hat{P}(Y|X)$或决策函数$Y=\hat{f}(X)$。条件概率分布$\hat{P}(Y|X)$或决策函数$Y=\hat{f}(X)$描述输入与输出随机变量之间的关系。在预测过程中，预测系统对于给定的测试样本集中的输入$x_{N+1}$，由模型$x_{N+1}=argmax\hat{P}(y|x_{N+1})$或$y_{N+1}=\hat{f}(y|x_{N+1})$给出相应的输出$y_{N+1}$
在监督学习中，假设训练数据与测试数据是依据联合概率分布$P(X,Y)$独立同分布产生的。
学习系统(也就是学习算法)试图通过训练数据集中的样本$(x_i,y_i)$带来的信息学习模型。具体地说，对输入$x_i$，一个具体的模型$y=f(x)$可以产生一个输出$f(x_i)$，而训练数据集中对应的输出是$y_i$。如果这个模型有很好的的预测能力，训练样本输出$y_i$和模型输出$f(x_i)$之间的差就应该足够小。学习系统通过不断地尝试，选取最好的模型，以便对训练数据集与足够好的预测，同时对未知的测试数据集的预测也有尽可能好的推广。

2 无监督学习
无监督学习（unsupervised learning）是指从无标注数据中学习预测模型的机器学习问题。无标注数据是自然得到的数据，预测模型表示数据的类别、转换或概率。无监督学习的本质是学习数据中的统计规律或潜在结构。
模型的输入与输出的所有可能取值的集合分别称为输入空间与输出空间。输入空间与输出空间可以是有限元素的集合，也可以是欧氏空间。每个输入是一个实例，由特征向量表示。每一个输出是对输入的分析结果，由输入的类别、转换或概率表示。模型可以实现对数据的聚类、降维或概率估计。
假设$\chi$是输入空间，$\zeta$是隐式结构空间。要学习的模型可以表示为函数$z=g(x)$，条件概率分布$P(z|x)$，或者条件概率分布$P(x|z)$的形式，其中$x\in \chi$是输入，$z\in \zeta$是输出。包含所有可能的模型的集合称为假设空间。无监督学习旨在从假设空间中选出给定评价标准下的最优模型。
无监督学习通常使用大量的无标注数据学习或训练，每一个样本是一个实例。训练数据表示为$U=\{x_1,x_2,\dots ,x_N\}$,其中$x_i,i=1,2,\dots ,N$表示样本。
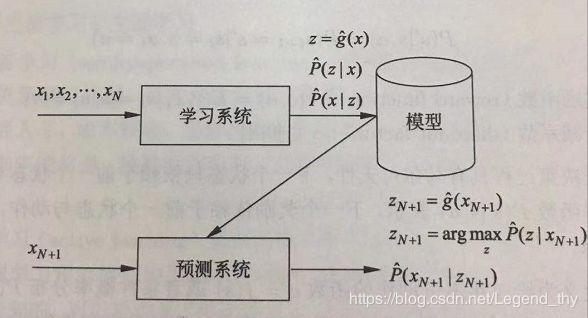
无监督学习可以用于对已有数据的分析，也可以用于对未来数据的预测。分析时使用学习得到的模型，即函数$z=\hat{g}(x)$,条件概率分布$\hat{P}(z|x)$,或者条件概率分布$\hat{P}(x|z)$。预测时，和监督学习有类似的流程。由学习系统与预测系统完成，如下图所示。

在学习过程中，学习系统从训练数据集学习，得到一个最优模型，表示为函数$z=\hat{g}(x)$，条件概率分布$\hat{P}(z|x)$或者条件概率分布$\hat{P}(x|z)$。在预测过程中，预测系统对与给定的输入$x_{(N+1)}$,由模型$z_{(N+1)}=\hat{g}(x_{(N+1)})$或者$z_{(N+1)}=argmax\hat{g}(x_{(N+1)})$给出相应的输出$z_{(N+1)}$,进行聚类或降维，或者由模型$\hat{P}(x|z)$给出输入的概率$\hat{P}(x_{(N+1)}|z_{(N+1)})$,进行概率估计。

3.强化学习
强化学习（reinforcement learning）是指智能系统在与环境的连续互动中学习最优行为策略机器学习问题。假设智能系统与环境的互动基于马尔可夫决策过程（Markov deccision process），智能系统能观测到的是与环境互动得到的数据序列。强化学习的本质是学习最优的序贯决策。
关于强化学习，目前暂不具体描述，在后期的学习过程中再进行详细论述。

生如夏花之绚烂，死如秋叶之静美。