Codeforces Round #645 (Div. 2)补题
好久没写题了……
最近好像能做出2D了,不过上分还是困难。
比赛传送门
这场出题人作的要死,对于题面内容这里不再提。
本场关键词
贪心、找规律、前缀和、二分
A.Park Lighting
题意
给你 n × m n\times m n×m的网格,你可以在两个网格之间的边上放一个灯,这个灯将会照亮这两个网格。
求出照亮所有的 n × m n\times m n×m个格子的最小需要的灯数。
思路
贪心,只要 n n n和 m m m中间有一个是偶数,那么答案就是总格子数除以二;如果都为奇数,那么先暂时去掉一行,将这部分如上计算,再对剩下这一行贪心考虑。
代码
#includeB.Maria Breaks the Self-isolation
题意
小M在办聚会,他现在想邀请 n n n个人,第 i i i个人有一个数值 a i a_i ai,表示当他到小M家时,如果在场的人(不包括他自己)达到 a i a_i ai,这个人就会留下。
求这场聚会最多可以邀请多少人,人数包括小M。
思路
排序之后贪心,如果 a i a_i ai被邀请了,那么数值小于等于 a i a_i ai的人一定也会被邀请。
代码
#includeC.Celex Update
题意
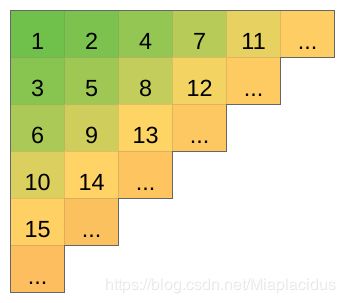
给你一个按照上图规律无限扩展的矩阵。
有 t t t组询问,每组 x 1 , y 1 , x 2 , y 2 x_1,y_1,x_2,y_2 x1,y1,x2,y2四个整数,保证 x 1 ≤ x 2 , y 1 ≤ y 2 x_1\le x_2\ ,y_1\le y_2 x1≤x2 ,y1≤y2,输出 ( x 1 , y 1 ) (x_1,y_1) (x1,y1)到 ( x 2 , y 2 ) (x_2,y_2) (x2,y2)的所有路径中,权值和不同的路径个数。
( x , y ) (x,y) (x,y)表示在第 x x x行 y y y列,只能向下或向右行走。
思路
找规律,组合数学
猜一发所有合法路径不会有权值和相同的情况,那么的话单纯计算路径数量只和 x 2 − x 1 x_2-x_1 x2−x1与 y 2 − y 1 y_2-y_1 y2−y1有关, a n s = ( x 2 − x 1 ) × ( y 2 − y 1 ) + 1 ans=(x_2-x_1)\times (y_2-y_1)+1 ans=(x2−x1)×(y2−y1)+1。
我也不知道怎么证明……
代码
#includeD.The Best Vacation
题意
你将选择一段时间和小C连续在一起度过 x x x天假期。
这里一年有 n n n个月,第 i i i个月有 d i d_i di天,当你在每个月第 j j j日和小C在一起时,他将给你 j j j个拥抱。
求你最多能得到多少拥抱数。
保证 1 ≤ x ≤ d 1 + d 2 + ⋯ + d n 1\le x\le d_1+d_2+\dots +d_n 1≤x≤d1+d2+⋯+dn
思路
贪心+前缀和+二分
首先 n n n已经达到了2e5,所以我们不可能枚举每一天作为起始点或者结束点。考虑枚举每个月时,可以发现将每个月最后一天作为结束点时是最优的,而因为 x ≤ d 1 + d 2 + ⋯ + d n x\le d_1+d_2+\dots +d_n x≤d1+d2+⋯+dn,所以度假期最多只可能跨一次年。
所以这里将 n n n翻倍,将相邻两年拼接起来,记 s u m 2 [ i ] sum2[i] sum2[i]为第 1 1 1月到第 i i i月的累积贡献, s u m 3 [ i ] sum3[i] sum3[i]为第 1 1 1月到第 i i i月的累积天数,当确定了结尾的月份时,在 s u m 3 sum3 sum3上二分出起始点所在月份,中间的月份的贡献通过 s u m 2 sum2 sum2查询,在起始点所在月份计算剩余天数的贡献。
记录其中出现的最大值即可。
代码
#includeE.Are You Fired?
哇这题好难搞,看了题解也不是很理解。
题意
给定一个长度为 n n n的数组,其中前 ⌈ n 2 ⌉ \left\lceil\dfrac{n}{2}\right\rceil ⌈2n⌉ 项中第 i i i项的值为 a i a_i ai,后面所有项值均为 x x x。
现在要你确定一个整数 k k k,使得数组中任意一个长度为 k k k的子段和 > 0 >0 >0,若不存在则输出 − 1 -1 −1。
思路
当有一个 k ′ ≤ ⌊ 1 n ⌋ k'\le \left\lfloor\dfrac{1}{n}\right\rfloor k′≤⌊n1⌋符合条件时,可以确定 k = 2 k ′ k=2k' k=2k′一定同样成立,这就说明假如存在解,就一定存在 k > n 2 k>\dfrac {n}{2} k>2n成立。
当 x ⩾ 0 x\geqslant 0 x⩾0时,可以确定最优情况为 k = n k=n k=n,判断即可。
否则接着深入研究,尝试找出对每个长度 k k k,出现的最小 k k k长度子段和。
记 p p p为长度为 k k k的字段和 s s s的差分数组, s 1 = a 1 + a 2 + ⋯ + a k s_1=a_1+a_2+\dots +a_k s1=a1+a2+⋯+ak。
而 s i + 1 = s i + a i + k − a i s_{i+1}=s_{i}+a_{i+k}-a_i si+1=si+ai+k−ai,因为 k > n 2 k>\dfrac {n}{2} k>2n,则 a i + k = x a_{i+k}=x ai+k=x。
即 p = [ s 1 , x − a 1 , x − a 2 , … , x − a n − k ] p=[s_1,x-a_1,x-a_2,\dots ,x-a_n-k] p=[s1,x−a1,x−a2,…,x−an−k]。
当 k k k增大了 1 1 1时,差分数组 p p p的首项 + x +x +x,并去掉最后一项。
任意 k k k长度的首项都可以用前缀和 s u m sum sum求出。
另开一个 d p dp dp数组, d p [ i ] dp[i] dp[i]表示对于 ∑ j = 1 i x − a j \sum\limits_{j=1}^ix-a_j j=1∑ix−aj过程中出现的最小和,用来表示 k = n − i k=n-i k=n−i的差分数组中出现的最小差分前缀和。
然后枚举下 k k k,检查一下 s u m [ k ] + d p [ n − k ] > 0 sum[k]+dp[n-k]>0 sum[k]+dp[n−k]>0,存在则直接输出。
代码
#include
void read(){}
template<typename T,typename... T2>inline void read(T &x,T2 &... oth) {
x=0; int ch=getchar(),f=0;
while(ch<'0'||ch>'9'){if (ch=='-') f=1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
if(f)x=-x;
read(oth...);
}
int a[maxn],sum[maxn];
signed main()
{
std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#ifdef DEBUG
freopen("input.in", "r", stdin);
// freopen("output.out", "w", stdout);
#endif
int n,lim,x;
cin>>n;
lim=n/2+(n%2);
for(int i=1;i<=lim;i++)
cin>>a[i],sum[i]=sum[i-1]+a[i];
cin>>x;
for(int i=lim+1;i<=n;i++)
sum[i]=sum[i-1]+(a[i]=x);
if(x>=0)
{
cout<<((sum[n]>0)?n:-1)<<endl;
return 0;
}
vector<int>dp(maxn,0);
for(int i=1,tot=0;i<=lim;i++)
{//dp[i]表示对长度为n-i的串,进行差分叠加过程中出现的最小和
tot+=x-a[i];//差分前缀和
dp[i]=min(dp[i-1],tot);
}
for(int k=lim;k<=n;k++)//枚举长度,首项[1,k]的和
{//k增大1时,右面有一个x并到了首项中
if(sum[k]+dp[n-k]>0)//前缀和,作为s的首项
{//如果其中最小和和
cout<<k<<endl;
return 0;
}
}
cout<<-1<<endl;
return 0;
}