超酷算法（1）：BK树 （及个人理解）

原文链接 ： 超酷算法（1）：BK树 - 博客 - 伯乐在线 http://blog.jobbole.com/78811/

看到上面地址里的一个BK算法，理解了半天……感觉算法用来查找不错，记下来加上个人一些理解。

本文由 伯乐在线 - 威士忌 翻译自 notdot。未经许可，禁止转载！
欢迎加入：翻译小组，通过翻译频道 贡献一份力量。

这是『超酷算法』系列的第一篇文章。基本上，任何一种算法我觉得都很酷，尤其是那些不那么明显简单的算法。

BK树或者称为Burkhard-Keller树，是一种基于树的数据结构，被设计于快速查找近似字符串匹配，比方说拼写检查器，或模糊查找，当搜索”aeek”时能返回”seek”和”peek”。为何BK-Trees这么酷，因为除了穷举搜索，没有其他显而易见的解决方法，并且它能以简单和优雅的方法大幅度提升搜索速度。

BK树在1973年由Burkhard和Keller第一次提出，论文在这《Some approaches to best match file searching》。这是网上唯一的ACM存档，需要订阅。更细节的内容，可以阅读这篇论文《Fast Approximate String Matching in a Dictionary》。

在定义BK树之前，我们需要预先定义一些操作。为了索引和搜索字典，我们需要一种比较字符串的方法。编辑距离（ Levenshtein Distance）是一种标准的方法，它用来表示经过插入、删除和替换操作从一个字符串转换到另外一个字符串的最小操作步数。其它字符串函数也同样可接受（比如将调换作为原子操作），只要能满足以下一些条件。

现在我们观察下编辑距离：构造一个度量空间（Metric Space），该空间内任何关系满足以下三条基本条件：

• d(x,y) = 0 <-> x = y (假如x与y的距离为0，则x=y)

• d(x,y) = d(y,x) (x到y的距离等同于y到x的距离)

• d(x,y) + d(y,z) >= d(x,z)

上述条件中的最后一条被叫做三角不等式（Triangle Inequality）。三角不等式表明x到z的路径不可能长于另一个中间点的任何路径（从x到y再到z）。看下三角形，你不可能从一点到另外一点的两侧再画出一条比它更短的边来。

编辑距离符合基于以上三条所构造的度量空间。请注意，有其它更为普遍的空间，比如欧几里得空间（Euclidian Space），编辑距离不是欧几里得的。既然我们了解了编辑距离（或者其它类似的字符串距离函数）所表达的度量的空间，再来看下Burkhard和Keller所观察到的关键结论。

假设现在我们有两个参数，query表示我们搜索的字符串，n表示字符串最大距离，我们可以拿任意字符串test来跟query进行比较。调用距离函数得到距离d，因为我们知道三角不等式是成立的，所以所有结果与test的距离最大为d+n，最小为d-n。

由此，BK树的构造就相当简单：每个节点有任意个子节点，每条边有个值表示编辑距离。所有子节点到父节点的边上标注n表示编辑距离恰好为n。比如，我们有棵树父节点是”book”和两个子节点”rook”和”nooks”，”book”到”rook”的边标号1，”book”到”nooks”的边上标号2。

从字典里构造好树后，取任意单词作为树的根节点。无论何时你想插入新单词时，计算该单词与根节点的编辑距离，并且查找数值为d(neweord, root)的边。递归得与各子节点进行比较，直到没有子节点，你就可以创建新的子节点并将新单词保存在那。比如，插入”boon”到刚才上述例子的树中，我们先检查根节点，查找d(“book”, “boon”) = 1的边，然后检查标号为1的边的子节点，得到单词”rook”。我们再计算距离d(“rook”, “boon”)=2，则将新单词插在”rook”之后，边标号为2。

在树中做查询，计算单词与根节点的编辑距离d，然后递归查找每个子节点标号为d-n到d+n（包含）的边。假如被检查的节点与搜索单词的距离d小于n，则返回该节点并继续查询。

BK树是多路查找树，并且是不规则的（但通常是平衡的）。试验表明，1个查询的搜索距离不会超过树的5-8%，并且2个错误查询的搜索距离不会超过树的17-25%，这可比检查每个节点改进了一大步啊！需要注意的是，如果要进行精确查找，也可以非常有效地通过简单地将n设置为0进行。

回顾这篇文章，写的有点长哈，似乎比我预期中的要复杂。希望你在阅读之后，也能感受到BK树的优雅和简单。

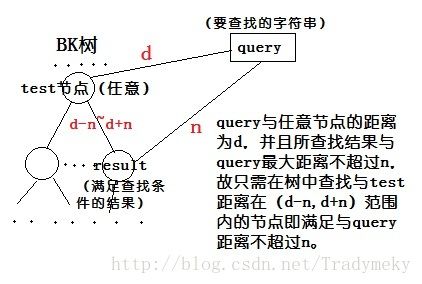
关于查找我画了个图，帮助理解：

文中查找说的不是很详细，写下自己理解的流程（有空编程实现）：

条件：一棵BK树，一个要查找的字符串query，与query最大的编辑距离n（n=0代表精确查找，n>0代表模糊查找）

step 1. query与根节点比较，编辑距离为d，然后找边值在范围（d-n,d+n）的子节点test（根据BK树结构特点，不在此范围代表这整个分支都不满足查找条件，可剪枝）；

step 2. 然后比较query与test节点的编辑距离，如果小于n，代表找到test节点符合查找要求，返回此节点；

step 3. 将当前的test节点当做根节点，返回step 1. 继续查找其子节点。递归以致遍历BK树，即可找到所有满足条件的结果。