浅论资产定价的两大基石 (I)
Two Pillars of Asset Pricing (I)
该文是Eugene Fama荣获2013年诺贝尔经济学奖时发表演讲的文字版,发表在次年6月的AER(American Economic Review)上。该文前半部分讨论有效市场假说,后半部分讨论资产定价模型,这两者被Fama形象地称为Two Pillars of Asset Pricing。本系列将对Fama这篇文章进行全文翻译,笔者希望以此对现代金融学资产定价理论的发展历程作一简要回顾,同时对此前本科阶段尚不甚明晰的问题予以厘清。本篇翻译了原文第一部分的前两节,剩余内容将在之后陆续完成。
原文链接:Two Pillars of Asset Pricing
By Eugene F. Fama
1. 有效市场
A. 早期研究
直至如今,芝大当年的PhD学生们仍不会忘记1962年这个颇具纪念意义的年份。彼时计算机刚刚进入他们的校园,将计量经济学家从古老的机械计算器中解放出来。自此以后,学者们能够快速地处理大量的数据(至少是按照以前的标准)。股票价格无疑是最容易获取的数据之一,随着计算机的引入,美国高校对股票价格数据的研究兴趣与日俱增,其中尤以芝大和MIT为最。彼时MIT的Franco Modigliani常来芝大造访其长期合作伙伴Merton Miller,因此这两所学校之间保持着密切的学术交流。
毫无疑问,有效市场假说(Efficient Market Hypothesis,EMH)一直是资产定价领域的核心问题,困难之处则在于如何检验这一假说。EMH认为市场确实做了它应该做的事(译者注:这是一个实证性问题),但是如果要检验EMH,我们必须得首先指定市场应该做什么(译者注:这是一个规范性问题),对于后者,自然需要资产定价模型来帮助我们指定,在市场均衡的条件下,资产的期望收益率应具有什么样的特征。要检验EMH是否成立,我们只需检验资产定价模型的结果是否与现实一致,如若不然,问题可能出在两个方面:其一,EMH确实不成立;其二,资产定价模型是有问题的。然而,我们并不清楚问题究竟出在哪个方面,这被称为联合假设问题(Joint Hypothesis Problem)(Fama,1970)。
假设时间离散, P t + 1 P_{t+1} Pt+1是 t + 1 t+1 t+1时刻所有资产的回报向量, f ( P t + 1 ∣ Θ t m ) f(P_{t+1}| \Theta_{tm}) f(Pt+1∣Θtm)是 P t + 1 P_{t+1} Pt+1基于 t t t时刻市场信息 Θ t m \Theta_{tm} Θtm的条件分布, f ( P t + 1 ∣ Θ t ) f(P_{t+1}| \Theta_t) f(Pt+1∣Θt)是 P t + 1 P_{t+1} Pt+1基于 t t t时刻全部可得信息 Θ t \Theta_t Θt的条件分布,那么EMH可表示为:
f ( P t + 1 ∣ Θ t m ) = f ( P t + 1 ∣ Θ t ) (1) f(P_{t+1}| \Theta_{tm}) = f(P_{t+1}| \Theta_t) \tag{1} f(Pt+1∣Θtm)=f(Pt+1∣Θt)(1)
我们更喜欢将EMH表示为收益率的形式。设 E ( R t + 1 ∣ Θ t m ) E(R_{t+1}|\Theta_{tm}) E(Rt+1∣Θtm)是基于市场信息的期望收益率, E ( R t + 1 ∣ Θ t ) E(R_{t+1}|\Theta_{t}) E(Rt+1∣Θt)是基于全部可得信息的期望收益率,那么EMH可表示为:
E ( R t + 1 ∣ Θ t m ) = E ( R t + 1 ∣ Θ t ) (2) E(R_{t+1}| \Theta_{tm}) = E(R_{t+1}| \Theta_t) \tag{2} E(Rt+1∣Θtm)=E(Rt+1∣Θt)(2)
f ( P t + 1 ∣ Θ t ) f(P_{t+1}| \Theta_t) f(Pt+1∣Θt)和 E ( R t + 1 ∣ Θ t ) E(R_{t+1}| \Theta_t) E(Rt+1∣Θt)是可观测的,而 f ( P t + 1 ∣ Θ t m ) f(P_{t+1}| \Theta_{tm}) f(Pt+1∣Θtm)和 E ( R t + 1 ∣ Θ t m ) E(R_{t+1}| \Theta_{tm}) E(Rt+1∣Θtm)则是不可观测的(因为现实中的股票价格是基于全部可得信息确定的,而非仅基于市场信息确定的)。这样一来,(1)式和(2)式就无从检验。若要检验EMH,我们必须指定 f ( P t + 1 ∣ Θ t m ) f(P_{t+1}| \Theta_{tm}) f(Pt+1∣Θtm)和 t t t时刻的均衡价格 P t P_t Pt之间的关系,这就需要一个资产定价模型来指定 E ( R t + 1 ∣ Θ t m ) E(R_{t+1}| \Theta_{tm}) E(Rt+1∣Θtm)所应当具有的特征。
在早期,EMH被诠释为基于历史信息无法预测未来的股票收益率。考虑一种最简单的资产定价模型:设期望收益率是恒定的:
E ( R t + 1 ∣ Θ t m ) = E ( R ) (3) E(R_{t+1}| \Theta_{tm}) = E(R) \tag{3} E(Rt+1∣Θtm)=E(R)(3)
如果市场是有效的,根据(2),我们有:
E ( R t + 1 ∣ Θ t ) = E ( R ) (4) E(R_{t+1}| \Theta_{t}) = E(R) \tag{4} E(Rt+1∣Θt)=E(R)(4)
于是我们可以根据(4)进行如下检验:构建 R t + 1 R_{t+1} Rt+1对 Θ t \Theta_{t} Θt中变量的回归方程,则解释变量前的系数应该不显著。如果系数显著,我们不知道问题出在(3)(即资产定价模型有问题),还是(1)和(2)(即EMH根本不成立),这就是联合假设问题。
如今看来,联合假设问题的存在似乎是显然的,或许早在Bachelier(1900),Muth(1961),Mandelbrot(1966)等文献中就已经含蓄地论及这一问题,但直至Fama(1970)才真正揭示了它在EMH研究中的重要性。EMH和资产定价模型是同一问题的两面:如果要检验EMH,必然也会同时对资产定价模型进行检验,例如许多早期的研究认为可以从收益率的样本自相关性入手检验EMH,其基本思想是基于EMH,资产收益率的样本自相关系数应该不显著,如果系数显著,则EMH不成立。这种检验方法忽视了一个问题,即它已经隐含地采用了如(3)所述的资产定价模型。
反过来,如果要检验资产定价模型,亦不可避免地要对EMH进行检验。常见的资产定价模型如CAPM,ICAPM,CCAPM等都假定投资者能够无成本地获得全部信息,且能够利用这些信息进行正确的投资决策——这是EMH的一种强版本。对这些资产定价模型进行检验的同时,也包含了对EMH的检验。
B. 事件研究
除了上一节讨论的早期研究方法,即考察未来收益率是否可以使用历史收益率进行预测,Fama et al.(1969)开创了一种新的方法用以检验EMH,这种方法称为事件研究法,即研究上市公司特定事件的发生对其股票价格的影响。具体而言,我们这篇文章研究的事件是股票分割(Stock Split)(译者注:股票分割即将一张较大面值的股票拆成几张较小面值的股票,此举对公司的资本结构不会产生任何影响,一般只会使发行在外的股票总数增加,但可以向投资者传递公司发展前景良好的信息,有助于提高投资者对公司的信心,所以是一种利好消息),样本期间是1926年-1960年。为了将特定事件对股票价格的影响从市场对股票价格的一般影响中分离出来(译者注:影响股票价格的因素可分为两种,其一是系统性的,即整个市场的波动,其二是非系统性的,即仅对某一特定公司或股票产生影响的事件或信息),我们使用了一个简单的市场模型:
R i t = a i + b i R M t + e i t (5) R_{it} = a_i + b_iR_{Mt} + e_{it} \tag{5} Rit=ai+biRMt+eit(5)
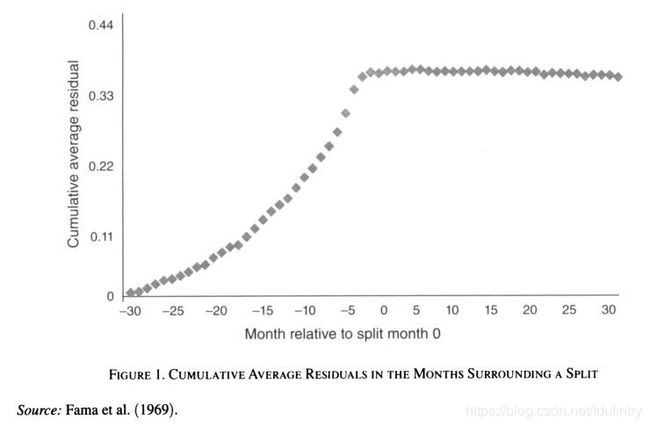
其中 R i t R_{it} Rit是股票 i i i的收益率, R M t R_{Mt} RMt是市场组合的收益率,残差 e i t e_{it} eit自然是股票 i i i的收益率中无法为市场因素所解释的部分,称为超常收益率。我们以事件发生的时间为中心,具体而言,将事件发生的那个月份记为 t = 0 t=0 t=0,事件发生之前的第 i i i个月记为 t = − i t=-i t=−i,之后第 i i i个月记为 t = i t=i t=i(对于不同的样本, t = 0 t=0 t=0其实对应着不同的日历时间)。在文中,我们考察了公告披露前后各30个月的超常收益率,并进行了样本上的平均,得到平均超常收益率(Average Abnormal Return,AAR)。为了便于观察,我们将AAR在时间序列上进行累加,得到累积平均超常收益率(Cumulative Average Abnormal Return,CAAR)。
论文的结论令人吃惊。CAAR在公告披露之前的数月便开始上升,而在公告披露之后则基本稳定,说明在公告披露以前,关于公司基本面的全部信息都已经被市场充分吸收,因此股票价格在公告披露之后没有进一步的反应,这正印证了EMH的预言。
我们的这篇论文催生了大量的后续研究,迄今为止,使用事件研究法对不同事件(包括业绩、并购、股利政策等等)进行的研究层出不穷,几乎所有相关研究都采用了我们提出的方法,其中很多较早的研究都得出了与我们相同的结论:市场对于事件的反应是迅速且完全的。
较早的研究主要针对以事件为中心的较短的时期,通常考察事件发生前后的若干天,此时资产定价模型相对来说不那么重要,这是因为股票价格受市场波动的影响显然远远小于受特定事件的影响。最近,行为金融领域的研究者开始把兴趣放在较长的时期,此时资产定价模型就变得十分重要,这是因为从长期来看,股票价格受市场波动的影响不容忽视。例如我们的论文假设回归方程(5)中的 a i a_i ai和 b i b_i bi是恒定的,如今它们则被普遍认为是时变的,而这就可能会影响我们的结论,感兴趣的读者可参考Fama(1998)。