ACM：平衡树(2)——Splay
题目来源：
HihoCoder1329
题目描述：
定义一个包含数字的集合，集合的初始情况为空。给定下面两种操作：题目描述：
插入：向集合中添加一个数字k。
询问：询问集合中不超过k的最大数字。
删除：删除落在区间[a, b]内的所有数字。
题目要求对于每次询问，输出对应的答案。
解答：
本题和HihoCoder1325类似，可以用之前介绍的Treap算法来解答。但Treap树堆有一个问题，节点的权值是随机生成的，因此对树的调整操作也是随机发生的，在某些情况下，Treap树同样也可能会退化为一条线，导致搜索效率降低。另外，本题添加了删除指定区间数据的操作，Treap树中对于删除操作也比较麻烦。
这里介绍另外一种平衡搜索树——Splay。
Splay树的操作：
Splay树和普通的二叉搜索树类似，Splay中文可以译为“伸展树”，它在基础的二叉搜索树的基础上，定义了4种新的操作，定义如下：
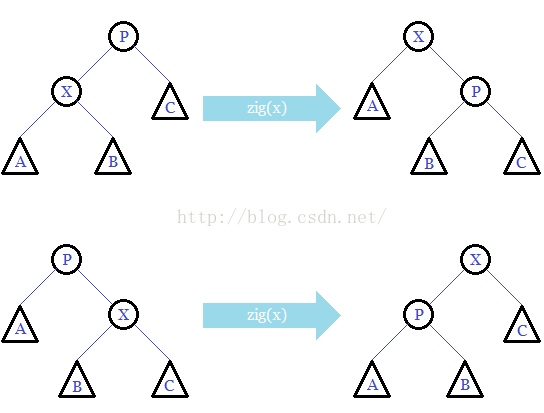
zig：
zig操作将树中的某个节点通过旋转提升一层，如下图：
zig-zig：
zig-zig操作将某个节点高度提升2层，执行该步骤的前提是：当前节点的父节点，以及当前节点的父节点的父节点均不为空，并且当前节点和其父节点同时为各自父节点的左孩子或右孩子。此时首先对于当前节点的父节点执行zig操作，然后在对当前节点执行zig操作。注意不是对于当前节进行两次zig操作，如下图：
zig-zag：
zig-zag操作和zig-zig操作类似。同样可以将节点高度提升2层。但该操作的前提是：当前节点的父节点，以及当前节点的父节点的父节点均不为空，并且当前节点和其父节点不是同时为各自父节点的左孩子或右孩子。即：当前节点是其父节点的左孩子并且父节点是其父节点的右孩子，或者当前节点是其父节点的右孩子并且父节点是其父节点的左孩子。zig-zag操作对当前节点连续执行两次zig操作将，节点高度提升2层。如下图：
splay：
基于以上的3种操作，我们可以定义Splay树的splay操作。该操作涉及到了两个节点A、B，其中节点A是节点B的祖先节点。通过Splay操作，可以将节点B转化为节点A的子节点。该过程通过对节点B反复进行以上的3中操作，使节点B的高度逐渐提升，直到节点B是节点A的孩子节点。具体步骤如下：
① 判定节点B的父节点是否为节点A。如果是，则算法结束，否则执行步骤②
② 找到节点B的父节点P，判定节点P的父节点是否为节点A。如果是，则对节点B执行zig操作；如果不是，则根据节点B、P以及P的父节点的关系，对节点B执行zig-zig操作或zig-zag操作。
③ 反复执行步骤①和②，直到算法结束。
注意：执行该操作的前提是：A节点必须是B节点的祖先节点。如果该条件不满足，则不可以执行splay操作。另外，如果想将某个节点变为根节点，则只要对空节点NULL和当前节点执行Splay操作即可。
·前驱和后继：
在解答本题过程中，用到操作还有查找某个节点的前驱节点和后继节点。该过程和普通的二叉查找树完全相同，简要说明如下：
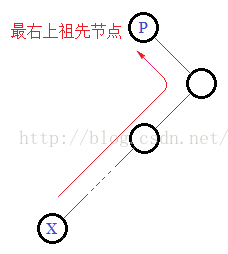
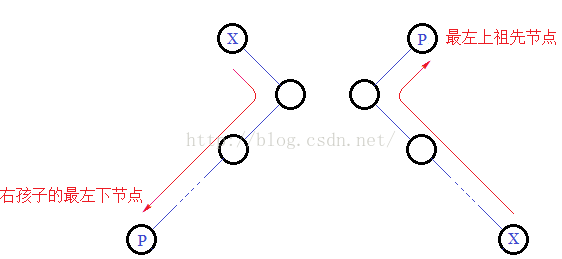
对于某个节点的前驱节点，就是它的左孩子的“最右下节点”，即从该节点的左孩子开始，顺着右孩子指针依次向下寻找，最后找到的节点就是其前驱节点：
·插入：
对于插入操作，和传统的二叉查找树的插入操作完全相同。不同的是，在插入操作完毕后对插入的节点执行Splay操作，使其成为当前Splay树的根节点。这样做的目的是平摊整个算法中不同操作的执行时间，使得整个算法的平摊效率趋近于O(lgn)。
·查找：
查找过程和普通的二叉查找树的过程也相同。在查找完成后，对当前找到的节点执行一次Splay操作，使其成为根节点，原因同上。
·删除：
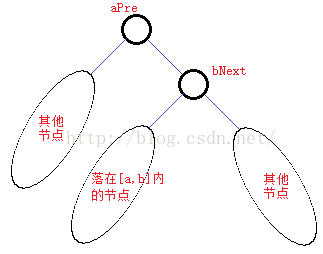
删除操作比较复杂，也是Splay树的优越性的所在。根据题意，这里的删除的操作是指删除树中所有落在指定区间[a,b]之内的节点。具体的操作步骤是：首先找出结点a的前驱结点aPre，以及结点b的后继节点bNext，然后利用Splay操作将aPre转化为树的根节点，然后将bNext节点转化为aPre的孩子节点。此时由于aPre < bNext, 因此，bNext一定是aPre的右孩子节点，此时，位于bNext的左子树中的节点就一定比apre大，同时又比bNext小，即落入区间[a,b]的节点，此时直接删除bNext的左子树即可。
删除节点的过程中可能会出现区间边界a,b不在树中的情况。 此时为了保证算法可以正确的进行。可以将a，b作为两个节点插入到树中，然后再执行删除的算法操作。另外在寻找前驱和后继节点的过程中，也会出现查找结果为空的情况，我们可以预先在树中插入一个极小的数和极大的数，这样就保证了所有有效节点的前驱和后继节点均为有效节点。保证算法的顺利进行。
但是注意，上文中插入的这些节点均不是有效的数据节点，是起到辅助作用的“虚”节点，因此在查询过程中，这些节点的值并不是有效的，应该略去。
输入输出格式：
输入：
第1行：1个正整数n，表示操作数量；
第2..n+1行：可能包含下面3种规则：
输出：1个字母'I'，紧接着1个数字k，表示插入一个数字k到树中，保证每个k都不相同。
1个字母'Q'，紧接着1个数字k。表示询问树中不超过k的最大数字；
1个字母'D'，紧接着2个数字a,b，表示删除树中在区间[a,b]的数。
若干行：每行1个整数，表示针对询问的回答，保证一定有合法的解。
数据范围：
100≤n≤200,000
1≤k≤1,000,000,000
程序代码：
/****************************************************/
/* File : Hiho_Week_103 */
/* Author : Zhang Yufei */
/* Date : 2016-07-09 */
/* Description : HihoCoder ACM program. (submit:g++)*/
/****************************************************/
#include
#include
#include
/*
* Define the node in splay tree.
* Parameters:
* @value: The value of this node.
* @max: The max value in the sub-tree.
* @tag: Mark if the node is real or fake.
* @left & @right: The left and right child.
* @parent: The parent node of this node.
*/
typedef struct node {
int value;
int max;
int tag;
struct node *left, *right;
struct node *parent;
} node;
// The root of splay tree.
node* root;
/*
* This function define the left rotate operation.
* Parameters:
* @cur: The current node to rotate.
* Returns:
* None.
*/
void left_rotate(node* cur) {
node* right = cur->right;
node* right_left = right->left;
node* parent = cur->parent;
right->parent = cur->parent;
if(parent != NULL) {
if(cur == parent->left) {
parent->left = right;
} else {
parent->right = right;
}
} else {
root = right;
}
right->left = cur;
cur->parent = right;
cur->right = right_left;
if(right_left != NULL) {
right_left->parent = cur;
}
if(cur->tag == 1) {
cur->max = cur->value;
} else {
cur->max = 0;
}
if(cur->left != NULL) {
if(cur->left->max > cur->max) {
cur->max = cur->left->max;
}
}
if(cur->right != NULL) {
if(cur->right->max > cur->max) {
cur->max = cur->right->max;
}
}
if(right->tag == 1) {
right->max = right->value;
} else {
right->max = 0;
}
if(right->left != NULL) {
if(right->left->max > right->max) {
right->max = right->left->max;
}
}
if(right->right != NULL) {
if(right->right->max > right->max) {
right->max = right->right->max;
}
}
}
/*
* This function define the right rotate operation.
* Parameters:
* @cur: The current node to rotate.
* Returns:
* None.
*/
void right_rotate(node* cur) {
node* left = cur->left;
node* left_right = left->right;
node* parent = cur->parent;
left->parent = cur->parent;
if(parent != NULL) {
if(cur == parent->left) {
parent->left = left;
} else {
parent->right = left;
}
} else {
root = left;
}
left->right = cur;
cur->parent = left;
cur->left = left_right;
if(left_right != NULL) {
left_right->parent = cur;
}
if(cur->tag == 1) {
cur->max = cur->value;
} else {
cur->max = 0;
}
if(cur->left != NULL) {
if(cur->left->max > cur->max) {
cur->max = cur->left->max;
}
}
if(cur->right != NULL) {
if(cur->right->max > cur->max) {
cur->max = cur->right->max;
}
}
if(left->tag == 1) {
left->max = left->value;
} else {
left->max = 0;
}
if(left->left != NULL) {
if(left->left->max > left->max) {
left->max = left->left->max;
}
}
if(left->right != NULL) {
if(left->right->max > left->max) {
left->max = left->right->max;
}
}
}
/*
* This function define the zig operation.
* Parameters:
* @cur: The current node to operate.
* Returns:
* None.
*/
void zig(node* cur) {
node* p = cur->parent;
if(cur == p->left) {
right_rotate(p);
} else {
left_rotate(p);
}
}
/*
* This function define the zig-zig operation.
* Parameters:
* @cur: The current node to operate.
* Returns:
* None.
*/
void zig_zig(node* cur) {
node *p = cur->parent;
node *pp = p->parent;
if(cur == p->left) {
right_rotate(pp);
right_rotate(p);
} else {
left_rotate(pp);
left_rotate(p);
}
}
/*
* This function define the zig-zag operation.
* Parameters:
* @cur: The current node to operate.
* Returns:
* None.
*/
void zig_zag(node* cur) {
node *p = cur->parent;
node *pp = p->parent;
if(cur == p->left) {
right_rotate(p);
left_rotate(pp);
} else {
left_rotate(p);
right_rotate(pp);
}
}
/*
* This function define the splay operation.
* Parameters:
* @cur: The current node to operate.
* @dst: The destination node.
* It's the parent node of @cur in final state.
* Returns:
* None.
*/
void splay(node* cur, node* dst) {
while(cur->parent != dst) {
node *p = cur->parent;
if(p->parent == dst) {
zig(cur);
} else {
node* pp = p->parent;
if(cur == p->left && p == pp->left ||
cur == p->right && p == pp->right) {
zig_zig(cur);
} else {
zig_zag(cur);
}
}
}
}
/*
* This function find the preview node of the current node.
* Parameters:
* @cur: The current node to search.
* Returns:
* The preview node of the current node.
*/
node* preview(node* cur) {
node* pre = cur->left;
if(pre != NULL) {
while(pre->right != NULL) {
pre = pre->right;
}
} else {
pre = cur;
while(pre != NULL) {
if(pre->parent != NULL &&
pre == pre->parent->right) {
pre = pre->parent;
break;
}
pre = pre->parent;
}
}
return pre;
}
/*
* This function find the successor node of the current node.
* Parameters:
* @cur: The current node to search.
* Returns:
* The successor node.
*/
node* successor(node *cur) {
node *suc = cur->right;
if(suc != NULL) {
while(suc->left != NULL) {
suc = suc->left;
}
} else {
suc = cur;
while(suc != NULL) {
if(suc->parent != NULL &&
suc == suc->parent->left) {
suc = suc->parent;
break;
}
suc = suc->parent;
}
}
return suc;
}
/*
* This function insert a node into the splay tree.
* Parameters:
* @ins: The node to insert.
* Returns:
* The inserted node.
*/
node* insert(node* ins) {
node* p = root;
node* pre = NULL;
while(p != NULL) {
pre = p;
if(ins->tag == 1) {
if(p->max < ins->value) {
p->max = ins->value;
}
}
if(ins->value > p->value) {
p = p->right;
} else if(ins->value < p->value) {
p = p->left;
} else {
if(ins->tag == 1) {
p->value = ins->value;
p->max = p->value;
p->tag = 1;
}
splay(p, NULL);
free(ins);
ins = p;
return ins;
}
}
if(pre != NULL) {
if(pre->value > ins->value) {
pre->left = ins;
} else {
pre->right = ins;
}
ins->parent = pre;
} else {
root = ins;
}
splay(ins, NULL);
return ins;
}
/*
* This function search the node according to the given range.
* Parameters:
* @s & @e: The left and right edge of range.
* Returns:
* The root of the sub-tree which contains nodes in the
* given range.
*/
node* search(int s, int e) {
node* s_node = (node*) malloc(sizeof(node));
s_node->value = s;
s_node->max = 0;
s_node->tag = 0;
s_node->left = s_node->right = s_node->parent = NULL;
node* e_node = (node*) malloc(sizeof(node));
e_node->value = e;
e_node->max = 0;
e_node->tag = 0;
e_node->left = e_node->right = e_node->parent = NULL;
s_node = insert(s_node);
e_node = insert(e_node);
node* s_pre = preview(s_node);
node* e_next = successor(e_node);
splay(s_pre, NULL);
splay(e_next, s_pre);
return e_next->left;
}
/*
* This function delete the nodes according to given range.
* Parameters:
* @s & @e: The left and right edge of range.
* Returns:
* None.
*/
void remove(int s, int e) {
node *del = search(s, e);
if(del != NULL) {
node* p = del->parent;
if(p != NULL) {
if(p->left == del) {
p->left = NULL;
} else {
p->right = NULL;
}
} else {
root = NULL;
}
while(p != NULL) {
if(p->tag == 1) {
p->max = p->value;
} else {
p->max = 0;
}
if(p->left != NULL) {
if(p->max < p->left->max) {
p->max = p->left->max;
}
}
if(p->right != NULL) {
if(p->max < p->right->max) {
p->max = p->right->max;
}
}
p = p->parent;
}
}
}
/*
* The main program.
*/
int main(void) {
int n;
scanf("%d", &n);
node* min = (node*) malloc(sizeof(node));
min->value = 0;
min->max = 0;
min->tag = 0;
min->left = min->right = min->parent = NULL;
node* max = (node*) malloc(sizeof(node));
max->value = 1000000001;
max->max = 0;
max->tag = 0;
max->left = max->right = max->parent = NULL;
insert(min);
insert(max);
for(int i = 0; i < n; i++) {
char op;
getchar();
scanf("%c", &op);
if(op == 'I') {
int k;
scanf("%d", &k);
node *ins = (node*) malloc(sizeof(node));
ins->value = k;
ins->max = k;
ins->tag = 1;
ins->left = ins->right = ins->parent = NULL;
insert(ins);
} else if(op == 'Q') {
int k;
scanf("%d", &k);
node* r = search(1, k);
printf("%d\n", r->max);
} else if(op == 'D') {
int a, b;
scanf("%d %d", &a, &b);
a = a > 1 ? a : 1;
b = b < 1000000000 ? b : 1000000000;
remove(a, b);
}
}
return 0;
}