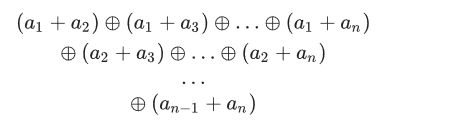Codeforces Round #626 (Div. 2) (D. Present 精妙异或处理 E. Instant Noodles(思维题))
题目链接
题意:给你n个数,让你求这个:
做法:一脸懵,这题咋写?参考题解
算是一种巧妙的运算方法吧,由于异或不满足分配律,所以不能化简做法。
那么直接来计算每一位是否有1贡献答案,那么加法是存在进位影响当前这位的,于是把每个数 低于当前位 的数 取出来,排下序,用简单的二分来统计多少是会进位的.
sum统计当前位1的个数,奇数个会贡献答案
枚举每个 低位ai 下面用b[i]代替,二分一下
若无进位,假设b[i]当前为1 就是 sum+=(当前位0的个数 1+0=1) 假设b[i]当前为0 就是 sum+=(当前位1的个数 0+1=1)
若有进位, 假设b[i]当前为1 就是 sum+=(当前位1的个数 1+1+1(进位1)=1) 假设b[i]当前为0 就是 sum+=(当前位0的个数 0+0+1(进位1)=1)
很妙的做法。。。
#include
#define rep(i,a,b) for(int i=a;i<=(b);++i)
#define mem(a,x) memset(a,x,sizeof(a))
#define pb push_back
#define pii pair
#define mk make_pair
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;}
int a[400005];
pii p[400005];
int l[400005];
int suffix0[400005];
int suffix1[400005];
void test_case() {
int n;
scanf("%d", &n);
for(int i = 1; i <= n; ++i)
scanf("%d", &a[i]);
int ans = 0;
for(int BIT = 0; BIT <= 26; ++BIT) {
int BITMASK = (1 << BIT) - 1;
for(int i = 1; i <= n; ++i) {
p[i].first = a[i] & BITMASK;//去掉高位只考虑低位
p[i].second = (a[i] >> BIT) & 1;//当前位 为0 或 为1
}
sort(p + 1, p + 1 + n);//按照低位从小到大排序
suffix0[n + 1] = 0;//后缀0
suffix1[n + 1] = 0;//后缀1
for(int i = n; i >= 1; --i) {
suffix0[i] = suffix0[i + 1] + (p[i].second == 0);
suffix1[i] = suffix1[i + 1] + (p[i].second == 1);
l[i] = p[i].first;
}
ll sum = 0;
//处理加法 加法存在低位进位影响该位 0+0+1=1 1+1+1=1
//和无进位也影响该位0+1=0 1+0=1
for(int i = 1; i <= n; ++i) {
int pos = upper_bound(l + i + 1, l + n + 1, BITMASK - l[i]) - l;//这样二分防止重复计算(例如a1+a2 a2+a1)
//当前i的低位和[i+1,pos]的数 相加是不会有进位的
//和[pos,n]的数相加 会有进位
//统计当前位置提供异或贡献1的个数
if(p[i].second == 0)//当前位0,
//和[i+1,pos] 当前位为1 相加 0+1=1
//和[pos,n] 当前位为0 相加 0+0+1=1
sum += suffix0[pos] + suffix1[i + 1] - suffix1[pos];
else//当前位1,
//和[i+1,pos] 当前位为0 相加 1+0=1
//和[pos,n] 当前位为1 相加 1+1+1=1
sum += suffix1[pos] + suffix0[i + 1] - suffix0[pos];
}
if(sum % 2 == 1)//奇数个1该位贡献答案
ans |= (1 << BIT);
}
printf("%d\n", ans);
}
int main()
{
test_case();
}
E. Instant Noodles
题意:给你一个二分图,求左侧端点的所有可能子集中的点相连的右侧端点的权值的和的最大公因数。
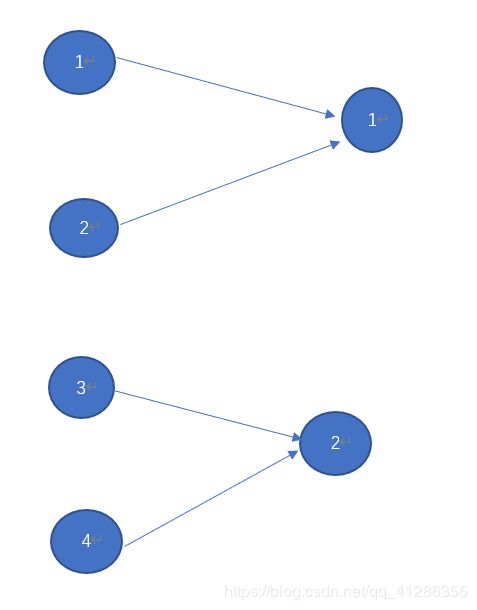
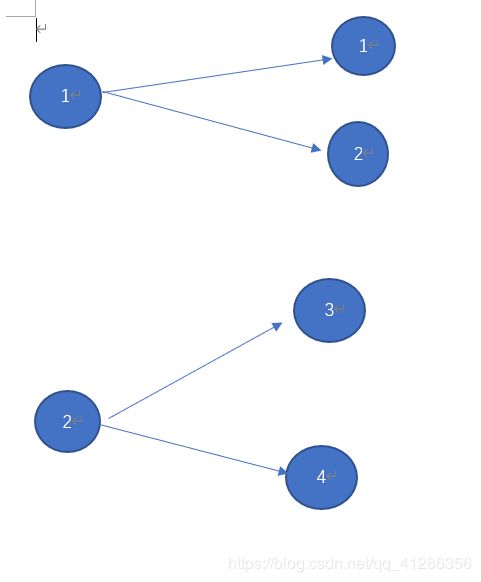
是不是很晕,别急,给你一组图就知道怎么写了:
这个答案就是gcd(val(1),val(2))
这组样例就是求gcd(val[1]+val[2],val[3]=val[4]);
做法:用vector保存每个右端点 的连左端点的有向边,然后用map保存 拥有相同左端点的右端点值的和,然后对map遍历 求gcd即可
#include
using namespace std;
const int N=5e5+10;
typedef long long ll;
ll c[N];
vector G[N];
int main(){
int _;cin>>_;while(_--){
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%lld",&c[i]);
G[i].clear();
}
for(int i=1;i<=m;i++){
int u,v;
scanf("%d%d",&u,&v);
G[v].push_back(u);
}
map ,ll> mp;
for(int i=1;i<=n;i++){
if(G[i].size()){
sort(G[i].begin(),G[i].end());
mp[G[i]]+=c[i];
}
}
ll ans=0;
for(auto i:mp){
//printf("se:%d\n",i.second);
ans=__gcd(ans,i.second);
}
cout<