Codeforces Round #626 (Div. 2）

A
这个似乎出过一遍了？选一个偶数或者两个奇数。

B
题意：
给你$n$个数$a_1,a_2,a_3,a_4......a_n$
再给你$m$个数$b_1,b_2.....b_m$
有一个矩形$n\cdot m$ 的矩形C，$C_{i,j}=a_i\cdot b_j$，且$a,b$中的数不是0，就是1，所以C中也是不是零就是1。
现在给你一个$k$，让你输出C中面积为$k$的矩形个数。
思路：
这个题目怎么说呢，说好想也好像，说不好想也不好想。。。。
首先，因为$a,b$中不是零就是1，所以C中为1的区域肯定是矩形，且大小为$a$中连续1的个数 * $b$中连续1的个数，有疑问可以画一下，到这儿还是比较好想的。然后接下来是重点。

假设a产生的连续的段为$x_1,x_2.....x_{cnt1}$
b产生连续的段为$y_1,y_2,y_3....y_{cnt2}$
这可以构成$cnt1\cdot cnt2$个矩形。
我们先按正解来，对于面积$k$的矩形，我们枚举边长，$<x,y>$
然后提前预处理好$a$中段对x的贡献，每一个为$x_i-x+1$；同理$y$也是这样。
答案就是$\sum _{i=1}^{cnt1}(x_i-x+1)\cdot \sum _{i=1}^{cnt2}(y_i-y+1)$。对于枚举边长，复杂度$O(N)$,预处理时间复杂度也是$O(N)$。
这样想似乎这个题目也就这样。。。。

但在比赛中我没想到直接枚举面积为$k$的矩形边长，而是枚举的$a\ast b$中可以产生的矩形，正如上文所说，$a,b$可以构成矩形为$cnt1\cdot cnt2$个。对于每个矩形我们算面积为$k$的贡献，怎么算呢？对于每个矩形$x_i\cdot y_i$，也是枚举边长，不过是枚举$x_i$的边长，看其是否可以构成面积为$k$的矩形，这里假设枚举$x_i$的边长为$x$，那么$y=k/x$。那么$x_i\cdot y_i$可以产生$<x,y>$的贡献为$(x_i-x+1)\cdot (y_i-y+1)$。其中$x$的范围$[1,x_i]$。我们不断累加贡献，也能得到贡献，但这样随机数据尚可，但最坏会被卡成$n^2$。值的一提的是我一开始看错范围以为4000。。。一直Wa和T，后经ZHJ提醒，数组开到40000，竟然以998ms的时间卡过，虽说后来重测被卡掉，但是这也不失是一件趣事。

赛后我以我的思路印证题解中代码，一直对上面正解中预处理边长累加那儿有疑惑，这很矛盾，在我的思路中，是枚举矩形然后对于这个矩形，在枚举边长，贡献是相乘后在相加，而题解中是相加后在相乘，这可能对别人来说很容易想透的，但对于我而言，这有点无法接受，人和人之间的思维方式真的有差别。

我按我的方式进行了思考，发现这两种思路是殊途同归的。我将用我的思路来解释正解。

假设$a$数组又连续段$a_1,a_2$,b数组有连续段$b_1,b_2$
我们可以构造$a_1$x$b_1$,$a_1$x$b_2$,$a_2$x$b_1$,$a_2$x$b_2$,四个矩形，原来是对每个矩形枚举边会超时，现在是对面积为$k$的矩形我们找边$<x,y>$
然后这四个矩形对其产生的贡献为
$(a_1-x+1)\cdot (b_1-y+1)+(a_1-x+1)\cdot (b_2-y+1)+(a_2-x+1)\cdot (b_1-y+1)+(a_2-x+1)\cdot (b_2-y+1)$
我们对上述式子进行提取公因式得
$((a_1-x+1)+(a_2-x+1))\cdot ((b_1-y+1)+(b_2-y+1))$
这个式子就是说对于边$<x,y>$ 结果是，a中所有段对$x$产生的贡献相加 乘以 b中所有段对$y$产生贡献的累加，这里所说的贡献可以当做产生多少$x$，产生多少$y$。

bool a[N],b[N];
ll q[N],p[N];
void init(int n,int m){ 
    int cnt1(0),cnt2(0);
    rep(i,1,n){
        if(a[i] == 0){
            for(int j =1 ;j <= cnt1;++j){
                q[j] += cnt1 - j + 1;
            }
            cnt1 = 0;
        }
        else cnt1 ++;
    }
    if(cnt1){
        rep(j,1,cnt1) q[j] += cnt1 - j + 1;
    } 
    rep(i,1,m){
        if(b[i] == 0) {
            for(int j = 1;j <= cnt2;++j) p[j] += cnt2 - j + 1;
            cnt2 = 0;
        }
        else cnt2++;
    }
    if(cnt2){
        rep(j,1,cnt2) p[j] += cnt2 - j + 1;
    }
}
int main(){
    int n = read(),m = read(),k =read();
    rep(i,1,n) a[i] = read();
    rep(i,1,m) b[i] = read();
    init(n,m); 
    ll ans = 0;
    for(int i = 1;i <= n;++i){
        if(k % i == 0){
            int x = i,y = k/i;
            if(y <= m) ans += q[x]*p[y];
        }
    }
    cout<< ans;
}

C
题意：
就是括号匹配，但是现在的问题是你可以通过对任意$[l,r]$排序，代价是这段的长度，来使的括号匹配。
思路：
首先就是若左右括号不等则一定不能匹配，否则一定可以。
我们设一个栈，然后从头遍历每个字符。
我们知道括号匹配的形式是$()$,所以我们考虑当前字符是否是’(’，如果是的话，看栈顶元素是否是’)’，如果是的话，这说明可以将这两个字符排序可以正确匹配，所以我们将$ans+=2$，并且删除栈顶元素；不是的话就将’(‘入栈。
如果当前元素是’)’ ，看栈顶是否是’('是的话就删除栈顶元素；否则入栈。
我们发现这样的匹配思路并没有错，而且代码还很好写。具体的怎么的正确我曾尝试证明，但是失败了。

stack<char> st;
int main(){
    int n = read();
    string s;
    cin >> s;
    int l = s.size();
    int cnt1(0),cnt2(0);
    rep(i,0,l-1){
        if(s[i]=='(') cnt1++;
        else cnt2++;
    }
    if(cnt1!=cnt2) return puts("-1"),0;
    int ans = 0;
    rep(i,0,l-1){
       if(s[i] =='('){
           if(st.size()&&st.top()==')'){st.pop();ans+=2;}
           else st.push('(');
       }
       else if(st.size()&&st.top()=='(') st.pop();
       else st.push(s[i]);
    }
    cout <<ans;
}

D
题意：
给你$n$个数，$a_1,a_2,a_3.....a_n$。然后问你两两之和的异或和是多少。

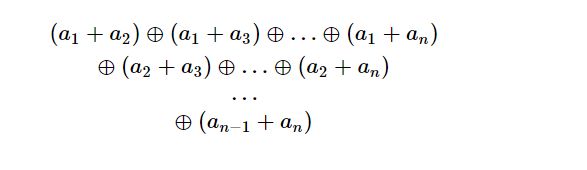
思路：
一般关于位运算的题目都是按位处理，我一开始想两两之和，那么从低到高统计1的个数，那么这一位1的个数乘0的个数，为当前为两两相加会产生1的个数，如果是奇数就对答案产生贡献，但是会有进位产生，不知道怎么处理。
题解给的方法很好，转化到了另一个问题，不用考虑进位了。
对于结果来说，第$k$位是否为1,与$k$之后位没有关系，所以直接$\%2^{k+1}$，去掉之后的位。
那么想要答案第$k$位为1的话，会有奇数个这样的项$(a_i+a_j)$会在第$k$位为1。而对于$a_i+a_j$来说，怎么判断它第$k$为是否为1呢？
我们分类讨论
1、$a_i,a_j$第$k$为上都没有1，那么若使得第$k$为上是1，则是下面这种：
最小：$2^k$

k+1	k	k-1	k-2	0
0	0	1	0	0
0	0	1	0	0
0	1	0	0	0

最大：$2^{k+1}-2$

k+1	k	k-1	k-2	0
0	0	1	1	1
0	0	1	1	1
0	1	1	1	0

2、$k$上至少有一位为1
最小：$2^k$

k+1	k	k-1	k-2	0
0	1	0	0	0
0	0	0	0	0
0	1	0	0	0

最大：$2^{k+1}-1$ （因为第$k$位上有一个1，为了不能产生进位，所以后面不能有进位，所以相加后的最大值后面全是1）

k+1	k	k-1	k-2	0
0	1	1	1	1
0	0	0	0	0
0	1	1	1	1

3、$k$上全为1
最小：$2^{k+1}+2^k$

k+1	k	k-1	k-2	0
0	1	1	0	0
0	1	1	0	0
1	1	0	0	0

最大：$2^{k+2}-2$

k+1	k	k-1	k-2	0
0	1	1	1	1
0	1	1	1	1
1	1	1	1	0

综上，若$a_i+a_j$相加结果在$[2^k,2^{k+1}-1]$ 或者$[2^{k+1}+2^k,2^{k+2}-2]$。则会在第$k$位上贡献1。
我们对于每一位，把模后的结果放到一个数组里，并从小到大排序，对于每个$i$，二分查找即可。
(这个二分我tm快改了一晚上，好吧，就是一晚上。。。。

int a[N];
vector<int> q;
int n;
int bina1(int x,int m,int num){//查询 <= num  的最大值
    int l = x+1,r = m;
    while(l < r){
        int mid = l + r +1 >> 1;
        if(q[x] + q[mid] <= num) l = mid;
        else r = mid -1;
    }
    return l;

}
int bina2(int x,int m,int num){//查询 >= num的最小值
    int l = x+1,r = m;
    while(l < r){
        int mid = l + r >>1;
        if(q[mid]+q[x] >= num) r = mid;
        else l = mid + 1;
    }
    return r;
}
bool ok(int p){//p为2^{k+1}
    q.clear();
    rep(i,1,n) q.push_back(a[i]%p);
    sort(q.begin(),q.end());
    int S = q.size();
    ll ans = 0;
    for(int i = 0;i < S-1;++i){//若区加相交，则可二分查找
        if(q[i+1]+q[i]<=p-1&&q[S-1]+q[i]>=p/2) ans += bina1(i,S-1,p-1) - bina2(i,S-1,p/2)+1;
        if(q[i+1]+q[i]<=p*2 -2&&q[S-1]+q[i]>=p+p/2) ans += bina1(i,S-1,p*2-2) - bina2(i,S-1,p+p/2)+1;
    }
    if(ans&1) return 1;//奇数个则产生贡献
    else return 0;
}
int main(){
    n = read();
    rep(i,1,n) a[i] = read();
    if(n == 2) return cout << (a[1]+a[2]) <<endl,0;
    ll ans = 0;
    for(int i = 0;i <= 25;i ++){
        if(ok(1<<(i+1))) ans |= 1<<i;
    }
    cout << ans;
}