Educational Codeforces Round 92 && Codeforces Round #660 (Div. 2)——CF初体验

Powered by:AB_IN 局外人

早上洛谷，下午OJ，晚上牛客，深夜CF。
好充实啊！

一开始卡的登不上，也提交不了。可以考虑镜像网站。
像我这种菜鸡就不玩Hack了。。

Educational Codeforces Round 92 (A-C)

A. LCM Problem

挑一个情况即可:l,2l，如果这个成立即可。

t=int(input())
while t>0:
    t-=1
    a,b=map(int,input().split())
    if b>=2*a:
        print(a,2*a)
    else:
        print("-1 -1")

B. Array Walk

这题挂的标签就是dp和贪心。我用的贪心做的。
题目要求可以左右横跳，而且一行不能出现连续向左跳两次的情况。
那么我们就在连续的两个数，它俩的和是所有连续两个数的和中最大的的 这两个数 左右横跳即可。
比如$15432$ 就在5,4这俩数左右横跳。
那么怎么解决这个问题呢?
那就通过枚举左右横跳的次数
先放上代码：

#include
using namespace std;
int t,n,m,k,z;
int a[100005],b[100005],sum[100005];
int main(){
	cin>>t;
	while(t--){
		cin>>n>>k>>z;
		for(int i=1;i<=n;i++){
			cin>>a[i];
			sum[i]=sum[i-1]+a[i];
		}
		for(int i=1;i<n;i++){
			b[i]=a[i]+a[i+1];
		}
		int mm=0;
		for(int i=z;i>=0;i--){
			int pos=k-2*i+1;
			if(pos<1)continue;
			int maxx=0;
			for(int j=1;j<=pos;j++){
				maxx=max(maxx,b[j]*i);//乘i就是在这横跳i次的结果
			}
			mm=max(mm,sum[pos]+maxx);
		}
		cout<<mm<<endl;
	}
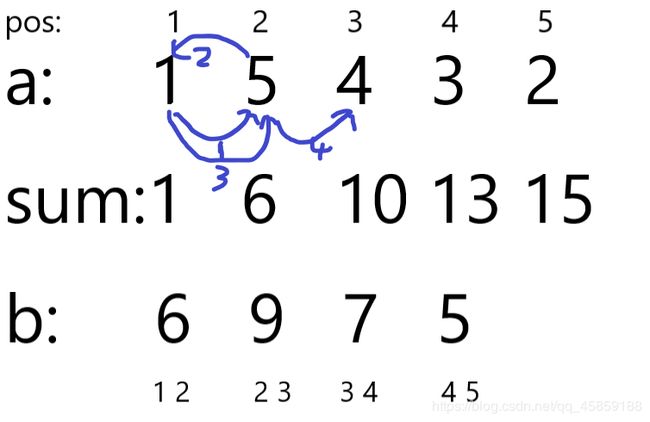
	return 0;
}

还是举$15432$这个例子：
允许走4步，可以左走1步。

首先我们先做出前缀和sum数组
还有两个数的和b数组
a为原数组
pos为数组下标

开始枚举z:

• 左走一步。
  既然能向左走一步，那么就是可以左右横跳一次，那么就用掉两步。
  那么一共有4步，用掉2步，剩2步往右走的。而走两步会使下标从1->3，所以pos=3。
  pos=3意味着什么，意味着你要左右横跳一次，那么就必须终点到pos=3的地方。
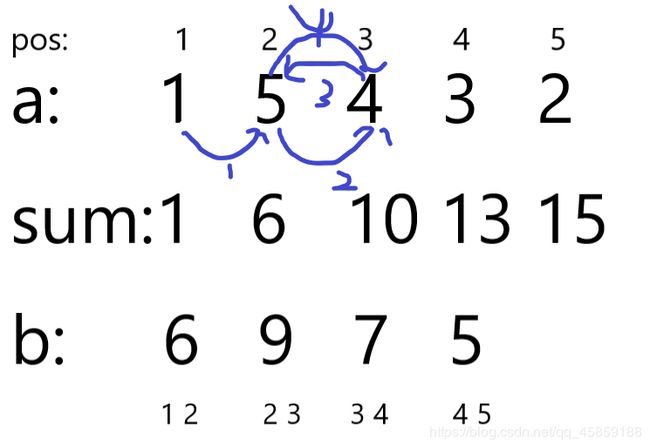
  好，下面我们就要抉择在哪两个数之间左右横跳，那么就看b数组。
  我们这个例子比较小，所以可以列举出来看看。

  • 在1 5 间
    

  • 在5 4 间
    

  • 在4 3 间
    

  显然在pos=3时，由b数组可以看出那两个数的和就是b数组的前三个。
  显然第二个情况最优，结果为19。

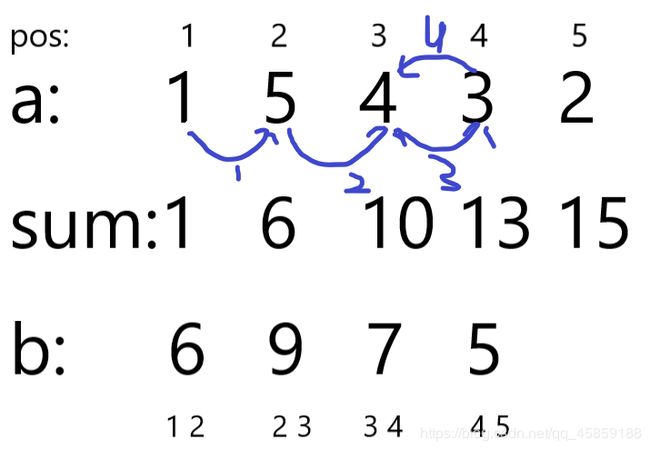
• 左走0步
  那么就是pos从1->5，结果是15。

所以最终结果是19。
再结合代码缕一缕就差不多了。

C. Good String

符合题意的字符串只有两种情况：

• 1.只有一种数字，一个数字一直循环。如111111。
• 2.只用两种数字，两个数字一直循环。如12121212。

所以枚举两个数字从0到9。（即枚举循环节）
核心环节：当第一个数字满足时，两个数字交换一下，继续往下匹配。
注意：（即solve函数的if语句）

• 第一种情况时，字符串长度是奇是偶都可以，两个数可以相等。
• 第二种情况时，字符串长度必须是偶数，两个数不能相等。

符合if语句时，说明不符合这个题循环节的定义，那么循环节长度就是1。

def solve(s, x, y):
    result = 0
    for a in s:
        if int(a)==x:
            result += 1
            x, y = y, x
    if x!=y and result%2==1:
        result = 1
    return result
 
t = int(input())
for _ in range(t):
    s = input()
    ans = 0
    for x in range(10):
        for y in range(10):
            ans = max(ans, solve(s, x, y))
    print(len(s)-ans)

牛客的pypy3慢，cf的pypy3快。把菜鸡搞蒙了。。。

Codeforces Round #660 (Div. 2) (A-B)

A. Captain Flint and Crew Recruitment

特殊情况搞一下就行了。前两个数放6和10，后两个数不等于6,10,0，这俩还不相等即可。
我写的有点麻烦了。。

#include 

using namespace std;
long long t,a,p[10]={0,14,15,21,22,26,33},tmp1,tmp2;
int main()
{
    cin>>t;
    while(t--){
        cin>>a;
        if(a<=30){
            printf("NO\n");
            continue;
        }
        else{
            int tmp=a-6-10;
            for(int i=1;i<=7;i++){
                tmp1=tmp-p[i];
                tmp2=p[i];
                if(tmp1!=tmp2&&tmp1!=6&&tmp1!=10&&tmp1!=0)
                    break;
            }
            printf("YES\n");
            printf("6 10 %lld %lld\n",tmp2,tmp1);
        }
    }
    return 0;
}

一开始不知道Hack这个机制，结果Hack错了。。。

B. Captain Flint and a Long Voyage

保证最后剩下的二进制数值r最大的同时，还需保证初始的x的值尽可能小。
最大：就要采用8（1001）9（1001）这两个长度为4的数。
最小：在末尾放8。比如n=5时 r=1001 1001 1001 100x xxxx(x为未知）
那么要x最小，就得x=1001 1001 1001 1000 1000。

t=int(input())
while t>0:
    t-=1
    k=int(input())
    a=(k+3)//4
    print('9'*(k-a)+'8'*a)

完结。