RegNet: Designing Network Design Spaces
Designing network design spaces是何凯明团队最近推出的一篇论文,目的是在探索网络搜索空间的设计。本论文和EfficientNet一样,也是假定网络的基本模块是不变的,不会去搜索基本模块的操作。文章中以残差bottleneck为基本模块,研究模块中bottleneck比例系数和group个数、以及每个stage的通道数和深度之间的设计,并逐步减小搜索空间的范围,最终得到一个小范围但是高性能的设计空间。
空间设计衡量工具
文章首先介绍了网络设计空间的衡量工具,叫做误差经验分布曲线(EDF)。这个曲线的计算方法是:从400MF计算量的设计空间中选取一堆网络模型、每个模型只训练10个epoch(目的是为了加快每个模型计算出准确率误差的速度),然后统计所有采样模型的准确率误差,计算公式为:
F ( e ) = 1 n ∑ i = 1 n 1 [ e i < e ] F(e)=\frac{1}{n}\sum_{i=1}^n1[e_i
这个公式表示的含义是,采样模型里面准确率误差小于 e e e占所有采样模型的比例。用坐标图可以表示为:

左边这个图就是误差EDF的函数曲线,中间和右边两图表示采样模型在深度和通道宽度两个维度上的误差分布。示例图中采样了500个模型。在后面中我们将会看到,每一次调整设计搜索空间时,均采样误差EDF来判断调整后设计空间的优劣。
AnyNet设计空间
AnyNet的设计空间有四个维度:模块个数 d d d(网络深度)、模块宽度 w w w(通道数)、模块中bottleneck的比例 b b b和group个数 g g g,文章中探讨的网络有4个stage,固定输入图片的大小为224,所以对一个网络来说,有16个自由度。初始的搜索空间定为: d i ≤ 16 d_i \leq 16 di≤16, w i ≤ 1024 w_i \leq 1024 wi≤1024(能被8整除), b i ∈ { 1 , 2 , 4 } b_i \in \{1, 2, 4\} bi∈{1,2,4}, g i ∈ { 1 , 2 , . . . , 32 } g_i \in \{1,2,...,32\} gi∈{1,2,...,32}, i i i表示stage序号。每次调整完设计空间后,均会从360MF到400MF的计算量范围中采样500个模型,训练10个epoch后来绘制EDF函数曲线。
最初的这个网络叫做AnyNetX,设计空间达到了 1 0 18 10^{18} 1018的可能性,所以需要采用一些方法来逐步减小AnyNet的搜索空间,主要有以下几个步骤:
- A n y N e t X A AnyNetX_A AnyNetXA. 初始的网络设计空间 A n y N e t X AnyNetX AnyNetX就叫做 A n y N e t X A AnyNetX_A AnyNetXA。
- A n y N e t X B AnyNetX_B AnyNetXB. 将所有stage的模块bottleneck比例统一设置,作者采用这个方法重新采样模型、训练和绘制EDF曲线,发现和 A n y N e t X A AnyNetX_A AnyNetXA中的EDF曲线基本上没有差别。这样就减少了3个搜索自由度,不用每个stage分别去搜索bottleneck比例,改成统一设置。
- A n y N e t X C AnyNetX_C AnyNetXC. 和步骤2中一样,统一设置每个stage的模块group参数,在步骤2的基础上重新采样、训练和得到EDF曲线,有意思的是,作者同样发现 A n y N e t X C AnyNetX_C AnyNetXC的EDF曲线和 A n y N e t X B AnyNetX_B AnyNetXB中几乎一致。所以在group这个参数上也可以统一设置,又减小了3个搜索自由度。
步骤2和步骤3的EDF曲线如下图所示:

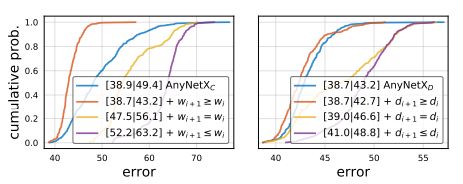
- A n y N e t X D AnyNetX_D AnyNetXD. 在步骤3的基础上,论文测试了 w i + 1 ≥ w i w_{i+1} \geq w_i wi+1≥wi情况下设计原则,结果惊奇地发现,居然比 A n y N e t X C AnyNetX_C AnyNetXC的EDF曲线更好。
- A n y N e t X E AnyNetX_E AnyNetXE. 在步骤4的基础上,采用了和 A n y N e t X D AnyNetX_D AnyNetXD相似的设计原则: d i + 1 ≥ d i d_{i+1} \geq d_i di+1≥di,结果又惊奇地发现,居然比 A n y N e t X D AnyNetX_D AnyNetXD的曲线更好。步骤4和步骤5让设计空间减小了 4 ! 4! 4!倍。
步骤4和步骤5的EDF曲线如下图所示:
RegNet设计空间
在 A n y N e t X E AnyNetX_E AnyNetXE的基础上,论文进一步探讨了搜索维度中每个stage中深度 d i d_i di和宽度 w i w_i wi之间的关系。作者在论文里面讲了一大堆,读者第一次看可能有点晕,其实简单地说就是采用数学建模的方法,用两个方程来表示:
u j = w 0 + w a ⋅ j w j = w 0 ⋅ w m [ s j ] u_j=w_0+w_a \cdot j \\ w_j=w_0 \cdot w_m^{[s_j]} uj=w0+wa⋅jwj=w0⋅wm[sj]
第一个方程中 u j u_j uj暂定表示为第 j j j个模块的通道数,它是一个等差的离散数列,但是在实际网络设计中,每个stage阶段的通道数是固定的,所以就设计了上面的第二个方程,其中 w j w_j wj表示第 j j j个block的通道数, [ s j ] [s_j] [sj]表示第 j j j个block属于哪一个stage,在这个方程里,每个stage不同block之间的通道数是固定。
我当时看到这边第一反应是只要有第二个方程就好了,第一个方程设计的意义何在?其实第一个方程是要用来计算每个stage的block个数 d i d_i di。在得到第 i i i个stage的通道数 w i w_i wi和第 i + 1 i+1 i+1个stage的通道数 w i + 1 w_{i+1} wi+1之后,只要计算出满足 w i ≤ u j ≤ w i + 1 w_i \leq u_j \leq w_{i+1} wi≤uj≤wi+1方程中 j j j的个数,就可以知道stage i i i有几个block了。
通过上面两个数学建模方程,论文每个stage模块的深度和宽度维度变成了对 d , w 0 , w a , w m d, w_0, w_a, w_m d,w0,wa,wm四个参数的搜索,再一次减小了搜索空间,将新的设计空间叫做 R e g N e t RegNet RegNet。作者在 d < 64 , w 0 , w a < 256 , 1.5 ≤ w m ≤ 3 d<64, w_0,w_a<256, 1.5 \leq w_m \leq 3 d<64,w0,wa<256,1.5≤wm≤3范围上进行采样、训练和绘制EDF,得到比 A n y N e t X E AnyNetX_E AnyNetXE更好的效果。

上面 A n y N e t X AnyNetX AnyNetX和 R e g N e t X RegNetX RegNetX是在4个stage,小计算量和少epoch的条件下进行的,作者为了验证这个方法的泛化性,在5个stage和更高计算量、更多epoch的条件下也做了实验,得到同样的结果,充分证明了这个方法的可扩展性。
实验
作者在论文中对 R e g N e t RegNet RegNet的参数做了一些限制,进一步减小了搜索的范围以及提升EDF曲线效果,这里就不一一列举了,有兴趣的读者在论文第4部分中查看。此外,作者还得到一些有趣的结论,比如发现好的模型bottleneck比例一般是1.0;对于 R e g N e t X RegNetX RegNetX网络来说,输入分辨率为 224 × 224 224 \times 224 224×224时是最佳的,这个和EfficientNet刚好相反。
作者在 R e g N e t X RegNetX RegNetX中加入了SE(Squeeze-and-Excitation)的操作,将这个网络的设计空间叫做 R e g N e t Y RegNetY RegNetY。
作者从各个计算量等级的 R e g N e t X RegNetX RegNetX和 R e g N e t Y RegNetY RegNetY中随机选取了25个网络模型进行训练,并挑选了其中最好的模型在ImageNet上重新训练5次100个epoch(获得鲁棒性结果),得到了下面两个表格的训练结果。作者在论文中特别提到,除了权重衰减之外,没有使用任何正则化和其他训练tricks。


好的效果肯定都是对比出来的,作者分别与移动端网络(~600MF)、ResNe(X)t和EfficientNet做了性能比较,前两个就不列出来了,有兴趣的在论文中查看,我们重点来看和EfficientNet的对比结果。
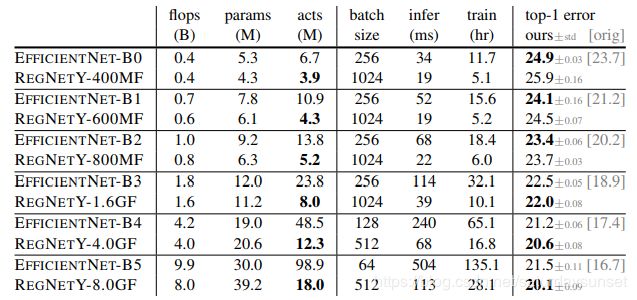
从上面这个表格可以看出,在相同等级计算量的条件下,EfficientNet-B0~B2比RegNetY更好一些,但是在更高计算量中,RegNetY开始超越了EfficientNet。除此之外,RegNetY无论是在模型参数大小还是训练推理时间上,都远远超过了EfficientNet。特别是RegNetY-8.0GF网络,不仅在精度上比EfficientNet-B5高出1.4个点,推理速度更是提升了接近5倍!