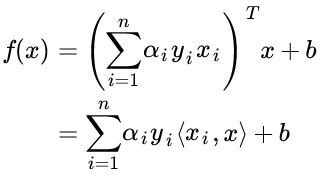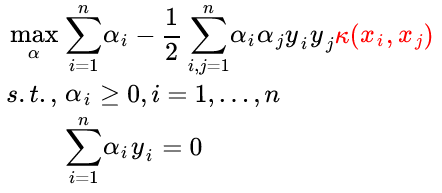SVM 是一块很大的内容,网上有写得非常精彩的博客。这篇博客目的不是详细阐述每一个理论和细节,而在于在不丢失重要推导步骤的条件下从宏观上把握 SVM 的思路。
1. 问题由来
SVM (支持向量机) 的主要思想是找到几何间隔最大的超平面对数据进行正确划分,与一般的线性分类器相比,这样的超平面理论上对未知的新实例具有更好的分类能力。公式表示如下:

: 所有点中最小的几何间隔, 实际上就是支持向量上的点的几何间隔
: 训练样本及对应标签,
, 作用是将第 i 个样本点的几何间隔转化为正数
公式的意思是假设每个训练样本点的几何间隔至少是
, 求
的最大值。
由于几何间隔(没帽子)和函数间隔(有帽子)的关系是:
最大化 ![]() 可以固定
可以固定 ![]() ,求 ||w|| 的最小值或者固定 ||w||, 求
,求 ||w|| 的最小值或者固定 ||w||, 求 ![]() 的最大值,一般选择前者: 固定函数间隔为 1, 将 \gamma = 1/||w|| 带入上式,同时为了计算方便, 目标函数等价于最小化 ||w||^2 ,约束优化问题转化为:
的最大值,一般选择前者: 固定函数间隔为 1, 将 \gamma = 1/||w|| 带入上式,同时为了计算方便, 目标函数等价于最小化 ||w||^2 ,约束优化问题转化为:
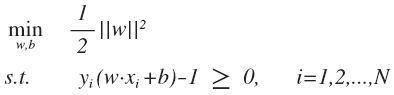
这是一个 QP 优化问题。
2. 对偶问题
利用拉格朗日乘子法将约束条件融入到目标函数:

SVM 的原始问题实际上是一个极小极大问题:
这个表达式有几个变量,先从哪一个着手?答案是 ![]() , 至于为什么,实际上是根据下面这个优化函数将原始问题的约束条件——函数间隔必须不小于 1 转化到拉格朗日乘子
, 至于为什么,实际上是根据下面这个优化函数将原始问题的约束条件——函数间隔必须不小于 1 转化到拉格朗日乘子 ![]() 向量上去的,先看函数的后面一部分:
向量上去的,先看函数的后面一部分:
很容易可以看出,如果样本点 xi 满足约束条件,即有 ![]() , 上式求最大,必定有
, 上式求最大,必定有 ![]() , alpha 与后面括号里面的式子必有一个为 0 (VI) 所有的样本点都满足约束条件,极小极大问题就转化为
, alpha 与后面括号里面的式子必有一个为 0 (VI) 所有的样本点都满足约束条件,极小极大问题就转化为 ![]() , 如果有一个样本点不满足约束条件,alpha 值取无穷大,上式将取无穷大,显然是没有意义的。实际上,这段论述就说明了原始问题具有 KKT 强对偶条件,对于原始问题来说需要满足的 KKT 条件有哪些呢?
, 如果有一个样本点不满足约束条件,alpha 值取无穷大,上式将取无穷大,显然是没有意义的。实际上,这段论述就说明了原始问题具有 KKT 强对偶条件,对于原始问题来说需要满足的 KKT 条件有哪些呢?
倒数两个条件是原始问题的条件,肯定成立。第一个条件是上面讨论过的条件:
- 当样本不在支持向量上,alpha 一定等于 0, w 在不等式2的内部,这是一个松的约束,L 函数就等于 1/2||w||^2 , 取它的偏导为0就可以了。
- 当样本点在支持向量上时, w 在不等式2的边界上,这是一个等式约束,这就和普通的拉格朗日等式约束相同,在最优点目标函数和约束条件函数的导数平行。用 wiki 的一张图来表示:
原始问题满足 KKT 条件,可以转化成一个最优解等价的对偶极大极小问题,先对极小部分求偏导:

得到对偶最优化问题:
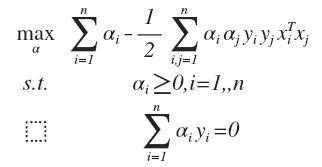
对于一个新来的样本,将上面 w 的值带入 f(x) = w^T·x + b, 可以知道要判断新来的点,我们只需要计算它与训练点的内积即可,这是 kernel trick 的关键:
3. 软间隔
软间隔问题是应对 outliers 的一种方法。软间隔问题可以建立目标函数:
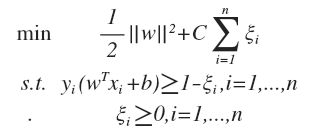
与硬间隔的优化方法相似,得到的解是:

4. Kernel Method
核方法是一种很巧妙的方法,既可以将特征映射到较高的维度,又可以地利用了 SVM 的内积运算避免了维度计算量的爆炸。最后的最优化问题与硬间隔优化问题相似,只要将两个样本的内积改为两个样本的核函数即可 (kernel substitution) :
当然,你也可以将两个样本的内积看做最简单的核函数。Kernel method 不仅可以用在 SVM 上,还可以用在 PCA、线性分类器上等,以后再专门写一篇 kernel method 的博客。
参考资料:
[1] pluskid 的博客
[2] 统计学习方法, 李航 著