学习笔记：二维凸包 Andrew算法

前置技能

• 向量叉积

例题

• 洛谷 P2742 【模板】二维凸包 / [USACO5.1]圈奶牛Fencing the Cows

参考代码

const int MAXN = 10005;
const double EPS = 1E-8;

int n,top;
double ans;

inline int dcmp(double x)
{
	if (fabs(x) < EPS) return 0;
	return x > 0 ? 1 : -1;
}//判断一个浮点数是等于0，大于0或小于0。

struct Vector
{
	double x,y;
	Vector(void) : x(0.0),y(0.0) {}
	Vector(double _x,double _y) : x(_x),y(_y) {}
	friend bool operator <(const Vector &VecA,const Vector &VecB)
	{
		if (VecA.x < VecB.x || (VecA.x == VecB.x && VecA.y < VecB.y)) return true;
		else return false;
	}//排序方法，找到基点。

	friend Vector operator -(const Vector &VecA,const Vector &VecB)
	{
		return Vector(VecA.x - VecB.x,VecA.y - VecB.y);
	}//向量减法。

	friend double operator ^(const Vector &VecA,const Vector &VecB)
	{
		return VecA.x * VecB.y - VecA.y * VecB.x;
	}//向量叉积。
	
	friend double dis(const Vector &VecA,const Vector &VecB)
	{
		return (VecA.x - VecB.x) * (VecA.x - VecB.x) + (VecA.y - VecB.y) * (VecA.y - VecB.y);
	}//两点间欧几里德距离。
}pos[MAXN],Stack[MAXN];

void init()
{
	scanf("%lld",&n);
	for (int i = 0;i < n;++i) scanf("%lf%lf",&pos[i].x,&pos[i].y);
	sort(pos,pos + n);
}

void work()
{
	for (int i = 0;i <= n - 1;++i)
	{
		while (top >= 2 && dcmp((Stack[top - 1] - Stack[top - 2]) ^ (pos[i] - Stack[top - 2])) <= 0) top--;
		Stack[top++] = pos[i];
	}
	int c = top;
	for (int i = n - 2;i >= 0;--i)
	{
		while (top >= c + 1 && dcmp((Stack[top - 1] - Stack[top - 2]) ^ (pos[i] - Stack[top - 2])) <= 0) top--;
		Stack[top++] = pos[i];
	}
	for (int i = 0;i <= top - 2;++i) ans += sqrt(dis(Stack[i],Stack[i + 1]));
	printf("%.2lf",ans);
}

分析

• pos[]：点坐标。以0作为基准下标。
• Stack[]：存放组成凸包的点。同样是0基准的。
• top：指向Stack的最后一个元素的后一个下标。

Andrew算法求凸包和Graham算法的区别是，后者以纵坐标为第一关键字，横坐标为第二关键字，找到的基点为$p6$；前者以横坐标为第一关键字，纵坐标为第二关键字，找到的基点为$p1$（两者都是较小者优先）。这样，对于Andrew算法而言，待扫描的点被分为$x$轴上下两部分，而Graham算法只需扫描基点上面的点。

对于一个凸包而言，若按照逆时针的顺序遍历组成它的每个点，显然点$p1$与其前一个点$p0$连成的直线$p1p0$总是在$p1$的下一个点$p2$的右侧。

以下图的凸包为例：

for (int i = 0;i <= n - 1;++i)
{
	while (top >= 2 && dcmp((Stack[top - 1] - Stack[top - 2]) ^ (pos[i] - Stack[top - 2])) <= 0) top--;
	Stack[top++] = pos[i];
}

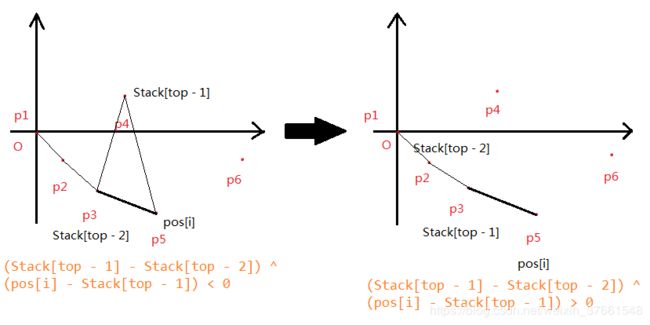
显然，Stack[]里至少应有两个点用来组成一个向量（top >= 2），再加上当前扫描到的点（pos[i]）和栈顶元素（Stack[top - 1]）组成另一个向量，由此判断这两个向量的位置关系。如果满足上面提到的条件，那么pos[i]就是组成凸包的元素（Stack[top++] = pos[i]）。

p.s. 作者看到有将$\le$号改成$＞$的，是因为他们这样写：

while (top >= 2 && dcmp((pos[i] - Stack[top - 2]) ^ (Stack[top - 1] - Stack[top - 2])) > 0) top--;

int c = top;
for (int i = n - 2;i >= 0;--i)
{
	while (top >= c + 1 && dcmp((Stack[top - 1] - Stack[top - 2]) ^ (pos[i] - Stack[top - 2])) <= 0) top--;
	Stack[top++] = pos[i];
}

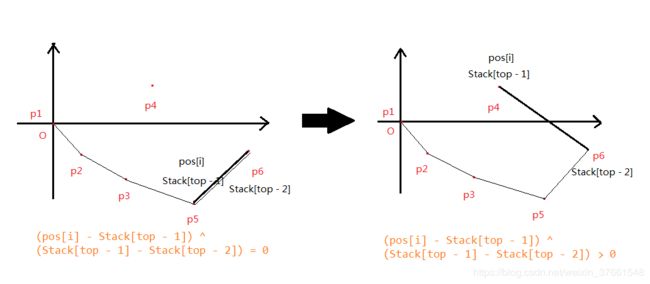//右图Stack[top - 1]和Stack[top - 2]应该分别是$p6$和$p5$。

从$p0$遍历到$p6$（$p_{n-1}$）只求出了下凸包，反过来按照同样的方法求出上凸包。为了不影响已经找到的下凸包，找上凸包时，对top值作出了限制（top >= c + 1）。

注意，根据Andrew算法，求完凸包后，Stack[]中会有7个点（$p1$被重复计算），此时top为8。

for (int i = 0;i <= top - 2;++i) ans += sqrt(dis(Stack[i],Stack[i + 1]));

最后统计凸包周长。由于top为8，我们又用到了Stack[i + 1]的值，所以$i$只枚举到top - 2。

---

向量操作

struct Vector
{
	double x,y;
	Vector(void) : x(0.0),y(0.0) {}
	Vector(double _x,double _y) : x(_x),y(_y) {}
};

friend Vector operator +(const Vector &VecA,const Vector &VecB)
{
	return Vector(VecA.x + VecB.x,VecA.y + VecB.y);
}//向量加法。

friend Vector operator -(const Vector &VecA,const Vector &VecB)
{
	return Vector(VecA.x - VecB.x,VecA.y - VecB.y);
}//向量减法。

friend double operator *(const Vector &VecA,const Vector &VecB)
{
	return VecA.x * VecB.x + VecA.y * VecB.y;
}//向量数量积。

friend double operator ^(const Vector &VecA,const Vector &VecB)
{
	return VecA.x * VecB.y - VecA.y * VecB.x;
}//向量叉积。

friend bool operator ==(const Vector &VecA,const Vector &VecB)
{
	return !dcmp(VecA.x - VecB.x) && !dcmp(VecA.y - VecB.y);
}//判断两个向量是否相等。

friend double dis(const Vector &VecA,const Vector &VecB)
{
	return (VecA.x - VecB.x) * (VecA.x - VecB.x) + (VecA.y - VecB.y) * (VecA.y - VecB.y);
}//两个点之间的欧几里德距离。

若有谬误，敬请斧正。