ACM暑期集训18

今天雨神开小灶讲了树形dp。

引入：

给你一棵n个点的树（1号点为根节点），求以点i为根的子树的大小

分析：

F[i]以点i为根的子树的点的个数 F[i] = 1+ΣF[k]  (k是i的儿子)

伪代码：

Void dfs(i )
{
  If(i是叶子节点)  f[i] = 1, 返回；
  for (k 是i的儿子) 
  {
       dfs(k);
       f[i]+=f[k];
  } 
  f[i]+=1;
}

例1.

给出一棵n个节点的树，让你删掉其中一个节点，使得删掉后形成的最大联通块最小

分析：

删除某个节点，他的儿子就成为独立的联通块，最大联通块就是max(x所有儿子联通块最大的size ,n-size[x]);

F[i]以将点i删掉以后最大联通块的大小

F[i] = max(n-tot[i], max(tot[k]))

K是I 的儿子  Tot[i]是以i为根的子树的大小 

void dfs(int x,int fa)
{
    size[x]=1;int maxx=0;
    for(int i=point[x];i;i=nxt[i])
      if (v[i]!=fa)
      {
        dfs(v[i],x);
        size[x]+=size[v[i]];
        maxx=max(maxx,size[v[i]]); 
      }
    maxx=max(maxx,n-size[x]);
    if (ans>maxx) ans=maxx,k=x;
}

例2：没有上司的舞会  （树的最大独立集）

题目大意： n个人形成一个关系树，每个节点代表一个人，节点的根表示这个人的唯一的直接上司，只有根没有上司。要求选取一部分人出来，使得每2个人之间不能有直接的上下级的关系，求最多能选多少个人出来，并且求出获得最大人数的选人方案是否唯一。

分析：

第一步：确定状态

用f[i][0]表示不选择i点时，i点及其子树能选出的最多人数，

f[i][1]表示选择i点时，i点及其子树的最多人数。

第二步：确定状态转移方程

f[i][0] = Σ(max (f[j][0], f[j][1]))

f[i][1] = 1+ Σf[j][0] (j是i的儿子！！)

边界：f[i][0] = 0, f[i][1] = 1  --------i是叶子节点

结果为max(f[root][0], f[root][1])

void dfs(int x)
{
    v[x] = 1;
    for (int i=1; i<=n; i++)
    {
        if ((!v[i]) && (fa[i] == x))
        {
            dfs(i);
            f[x][0] += max(f[i][1], f[i][0]);
            f[x][1] += f[i][0];
        }
    }
}

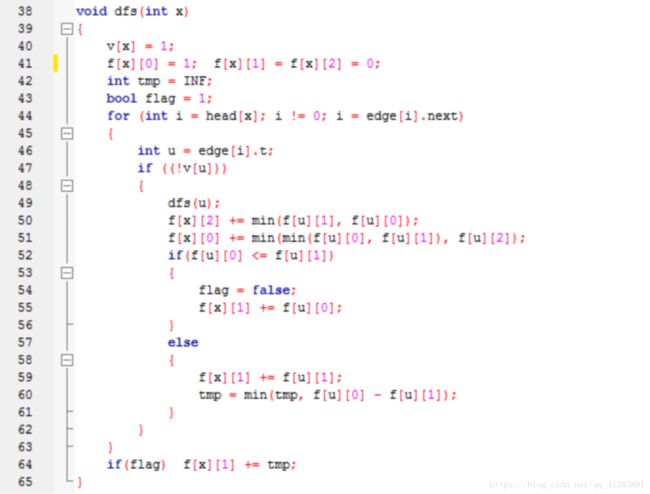
例3：Strategic game （树的最小点覆盖）

一城堡的所有的道路形成一个n个节点的树，如果在一个节点上放上一个士兵，那么和这个节点相连的边就会被看守住，问把所有边看守住最少需要放多少士兵。

分析：

第一步：确定状态

f[x][1]以x为根的子树在x上放置的士兵的最少所需的士兵数目

f[x][0]以x为根的子树x上不放置的士兵的最少所需的士兵数目

第二步：确定状态转移方程

f[x][1] =1 + Σ min(f[i][0],f[i][1]) // x上放置的士兵，于是它的儿子们可放可不放！

f[x][0] = Σ f[i][1]           //x上不放置的士兵，它的儿子们都必须放！ (i是x的儿子！！)

结果为min(f[root][0], f[root][1])

void dfs(long x)
{
    v[x] = 1;
    for (long i=0; i

例4：Cell Phone Network （树的最小支配集）

给你一棵无向树，问你最少用多少个点可以覆盖掉所有其他的点。 （一个点被盖，它自己和与它相邻的点都算被覆盖）

分析：

第一步：确定状态

①dp[i][0]：选点i，并且以点i为根的子树都被覆盖了。

②dp[i][1]：不选点i，i被其儿子覆盖

③dp[i][2]：不选点i，i没有被子节点覆盖（被其父亲覆盖）

第二步：确定状态转移方程

dp[i][0]=1+Σmin(dp[u][0],dp[u][1],dp[u][2]) （u是i的儿子）

dp[i][2]=Σ(dp[u][1])

对于dp[i][1]的讨论稍微复杂一点——他的所有儿子里面必须有一个取dp[u][1]  

那么：if(i没有子节点)dp[i][1]=INF

     else dp[i][1]=Σmin(dp[u][0],dp[u][1])+inc

其中对于inc有：

 if(上面式子中的Σmin(dp[u][0],dp[u][1])中包含某个dp[u][0])inc=0;

       else inc=min(dp[u][0]-dp[u][1])。

例5：二叉苹果树

有一棵苹果树，苹果树的是一棵二叉树，共N个节点，树节点编号为1~N，编号为1的节点为树根，边可理解为树的分枝，每个分支都长着若干个苹果，现在要要求减去若干个分支，保留M个分支，要求这M个分支的苹果数量最多。

分析：

第一步：确定状态

f[u][j]表示在以u为根的子树保留j个分支可以得到的最大苹果数量

第二步：确定状态转移方程

f[u][j]=f[r][j-1]+a[r] （如果切的是连接左子树的边）

f[u][j]=f[l][j-1]+a[l] （如果切的是连接右子树的边）

f[u][j]=max( f[r][k]+f[l][j-k-2]+a[r] +a[l] )   (1=

 

如果是多叉树怎么办？

F[u][j] = max(f[u][k] + f[v][j – k - 1] + W)  v分别是u的儿子，w为u到v边上的苹果数目, k属于[0, j]

void dfs(int u)
{
     vis[u]=1;
      int i,v,w,j,k,son=0;
      for(i=head[u];i!=-1;i=e[i].next)
      {
	 v=e[i].ed;w=e[i].w;
	 if(vis[v]==1)continue;
	 dfs(v);
	 for(k=m;k>=1;k--)
	 {
	       for(j=1;j<=k;j++)//在v节点的子树中选择j条边
                         if(f[u][k]

例6：树的直径

树的直径定义为：树中距离最远的两个点的距离

两次dfs即可求出树的直径，详见传送门

例7：

题目大意：给定n个敌方据点，1为司令部，其他点各有一条边相连构成一棵树，每条边都有一个权值cost表示破坏这条边的费用，叶子节点为前线。现要切断前线和司令部的联系，每次切断边的费用不能超过上限limit，问切断所有前线与司令部联系所花费的总费用少于m时的最小limit。1<=n<=1000,1<=m<=100万

分析：

最大值最小—— 二分

怎么检验？ f

[i]为切断i的所有子孙叶子所花费的最小费用

dp[i]+=min(dp[k],dist[i][k] )    (dist[i][k] <= limit )

else dp[i] += dp[k]

例8：消防站

Z国有n个城市，从1到n给这些城市编号。城市之间连着高速公路，并且每两个城市之间有且只有一条通路。不同的高速公路可能有不同的长度。最近Z国经常发生火灾，所以当地政府决定在某些城市修建一些消防站。在城市k修建一个消防站须要花费大小为W的费用。函数W对于不同的城市可能有不同的取值。如果在城市k没有消防站，那么它到离它最近的消防站的距离不能超过 。每个城市在不超过距离Di的前提下，必须选择最近的消防站作为负责站。函数D对于不同的城市可能有不同的取值。为了节省钱，当地政府希望你用最少的总费用修建一些消防站，并且使得这些消防站满足上述的要求。

分析：

令f[i][j]表示i是被在结点j修建的消防站保护的，且i的子树被子树中的消防站或者j点的消防站保护的最小花费

Best [i]表示在以i为根的子树中，修建合符要求的消防站的最小费用。

Best[i] = f[i][k]  (k在i的子树内)

①当 dist[i][j] > Di时， f[i][j] = ∞

②当 dist[i][j] <=Di时，

⑴当j在以i为根的子树外时，f[i][j] =  Σmin(best[k], f[k][j])

⑵当i= j时，f[i][j] =  Σmin(best[k], f[k][j]) + cost[i]

⑶当i!=j并且j在以i为根的子树内时，f[i][j] = f[child][j]+Σmin(best[k], f[k][j])  (k != child)(child是i的直接儿子，j的祖先，或者j自己)