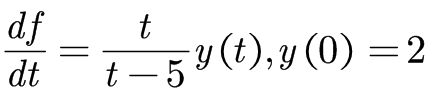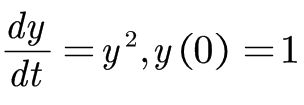MATLAB与高等数学--常微分方程(ODE)的求解
常微分方程(ODE)的求解
常微分方程的求解使用dsolve命令
>> clear;
>> syms y(t) a;
>> q = diff(y,t,1)==a*y;
>> s = solve(q)
s =
C1*exp(a*t)
我们还可以指定常数值，带入：
>> C1 = 2;a = 4;
>> f = subs(s)
f =
2*exp(4*t)
初始条件作为参数放在后面，注意要使用赋值号。：
>> syms f(t) ;
>> q = diff(f,t,1)==f*t/(t-5);
>> s = dsolve(q,f(0)==2)
s =
-(2*exp(t + 5*log(- 5 + t)))/3125
二阶或者更高阶的处理方法类似：
- 使用
syms声明变量:
由于求解的是微分方程，所以f跟自变量是函数关系，但具体的表达式不清楚，所以我们可以直接声明：
syms f(t)，后面也可以跟上其它未知数。 - 根据阶数使用
diff命令：
固定用法:
diff(f,t,n)
f代表因变量，t代表自变量，也就是对谁求导，n是方程的阶数。
- 然后写出等式：
固定格式：
q = 方程左边==方程右边
- 然后使用
dsolve命令，并将结果返回给一个变量
当初始条件中含有一阶导数的条件时，我们先要把一阶导数表示出来，然后将条件带入：
>> syms f(t);
>> q = diff(f,t,2)-f==0;
>> cond1 = f(0)==-1;
>> cond2 = diff(f,t,1);
>> s = dsolve(q,cond1,cond2(0)==2)
s =
exp(t)/2 - (3*exp(-t))/2
例题：求下列方程的解并绘制t在0～10之间的图像
>> syms f(t);
>> q = diff(f,t,1)==t+3;
>> cond = f(0)==7;
>> s = dsolve(q,cond)
s =
(t*(6 + t))/2 + 7
绘制图形：
例题：求解下面的方程并绘制图像以及它的渐近线。
>> syms y(t) ;
>> q = diff(y,t,1)==y.^2;
>> cond1 = y(0)==1;
>> s = dsolve(q,cond1)
s =
-1/(- 1 + t)
绘制图形：
我们看到解s，所以渐近线只能出现在分母等于0的地方，我们把分母单独拿出来，求它的根：
>> d = (t-1);
>> root = solve(d==0)
root =
1
接下来绘制渐近线：
>> plot(double(root)*[1 1],[-2 2],'--')
例题：求解下式并绘制t在-50～50之间的图像。
dsolve默认使用t作为独立变量，但题目中的变量为x，所以我们要更改自变量。
>> syms f(x);
>> q = diff(f,x,2)-(sin(x)/x).*(1-2/(x.^2))-2*cos(x)/(x.^2)==0;
>> cond1 = f(0)==2;
>> cond2 = diff(f,x,1);
>> s = dsolve(q,cond1,cond2(0)==0)
s =
3 - sin(x)/x
-
还是要重复提醒的是，要注意赋值号跟等号：
一般格式是：方程=方程左边公式==方程右边公式
绘制函数图像：
例题：求方程的通解并且在-1~1范围内绘制C1=0，10，20，30的图像
方程的通解：
>> syms y(t);
>> q = diff(y,t,1)==-y/(sqrt(1-t.^2));
>> s = dsolve(q)
s =
C1*exp(-asin(t))
然后我们带入C1的值求方程的特解：
>> C1 = [0 10 20 30];
>> f = subs(s)
f =
[ 0, 10*exp(-asin(t)), 20*exp(-asin(t)), 30*exp(-asin(t))]
C1=0图像：
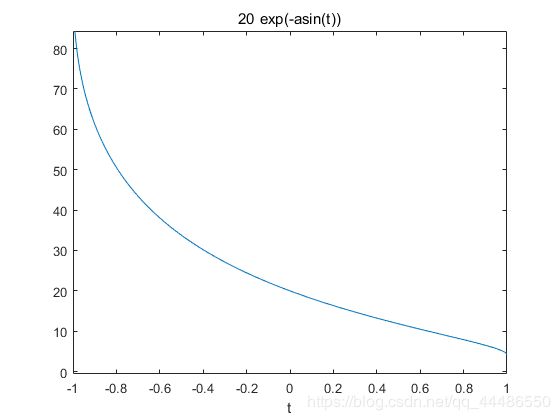
C1=10图像：
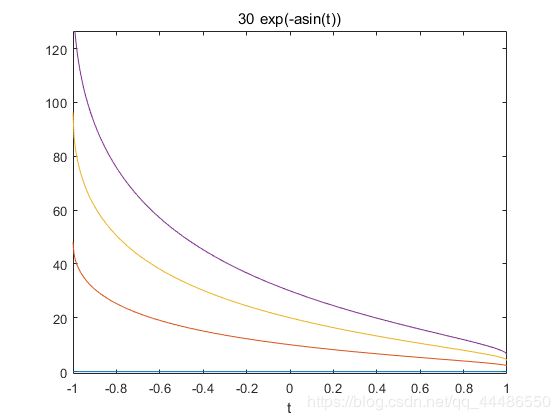
C1=20图像：
C1=30图像：
上面的方法未免过于繁琐，我们可以使用循环配合subs命令来逐个将值代入函数，然后再循环中使用hold on 命令来依次绘图。
syms y(t);
q = diff(y,t,1)==-y/(sqrt(1-t.^2));
s = dsolve(q);
for i = 0:10:30
f = subs(s,'C1',i);
ezplot(f)
hold on;
end
注意：
f = subs(s,'C1',i);
此命令的意思是将用i为C1赋值并且带入s的表达式中。
例题：以不同的初始值绘制图像，设y(0)=0.2,...,2.0,增量取0.2，
clear;
syms y(t);
q = diff(y,t,1)==-2*t.*(y.^2);
for i = 0.2:0.2:2.0
cond = y(0)==i;
s = dsolve(q,cond);
ezplot(s);
hold on;
end
或者使用subs命令：
clear;
syms y(t) a;
q = diff(y,t,1)==-2*t.*(y.^2);
cond = y(0)==a;
f = dsolve(q,cond);
for i = 0.2:0.2:2.0
tempt = subs(f,a,i);
ezplot(tempt);
hold on;
end
