数据结构（二十） -- C语言版 -- 树 - 霍夫曼树（哈夫曼树、赫夫曼树、最优二叉树）、霍夫曼编码

零、读前说明

• 本文中所有设计的代码均通过测试，并且在功能性方面均实现应有的功能。
• 设计的代码并非全部公开，部分无关紧要代码并没有贴出来。
• 如果你也对此感兴趣、也想测试源码的话，可以私聊我，非常欢迎一起探讨学习。
• 由于时间、水平、精力有限，文中难免会出现不准确、甚至错误的地方，也很欢迎大佬看见的话批评指正。
• 嘻嘻。。。。 。。。。。。。。收！

一、概述

  漂亮国数学家霍夫曼（David Huffman），也称赫夫曼、哈夫曼等。他在1952年发明了霍夫曼编码，所以就将在编码中用到的特殊的二叉树称为霍夫曼树，编码方式称为霍夫曼编码。膜拜！

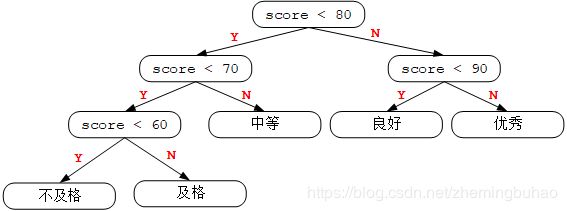
  在了解之前，我们先来看看从小就被支配的考试的分数，往往因为那么几分经常喜提男女混合双打套餐一份。在我们学习编程不久，也会有这样一个简单的代码来练习手法，每次编写这样的程序都会想到：为什么 60 分才及格呢 ??(͡° ͜ʖ ͡°)

if(score < 60) printf("不及格\n");
else if(score < 70) printf("及格\n");
else if(score < 80) printf("中等\n");
else if(score < 90) printf("良好\n");
else printf("优秀\n");

  程序运行的结果肯定是没有任何问题的，每次运行出正确的结果，心里的自豪感爆棚呀有没有！！ ≧◠◡◠≦✌
  

图1.1 成绩分布示意图

  
   但是现在学习了数据结构与算法之后，我们发现了端倪：通常学生的成绩呈现正态分布，也就是说 70 - 80 分的学生占大多数，而少于 60 分或者多于 90 分毕竟是少数，所以对于 70 - 80 分的这个分支，通常需要判断三次才能到，那么消耗的时间也就也多，那我们就会发现，这个程序运行的效率有问题，强迫症告诉我，搞他！！！

  那么既然这样的话， 我们来进行简单的计算一下，假设成绩的分布的占比为下表所示这样。

表1.1 分数占比分布表

分 数	0 ~ 59	60 ~ 69	70 ~ 79	80 ~ 89	90 ~ 100
占 比	5%	15%	40%	30%	10%

  假设有100个学生，那么根据上面的程序总共需要判断的次数为（占比 乘以 判断次数，且注意最后一个 else 不占次数）：

5 * 1 + 15 * 2 + 40 * 3 + 30 * 4 + 10 * 4 = 315 (次)   

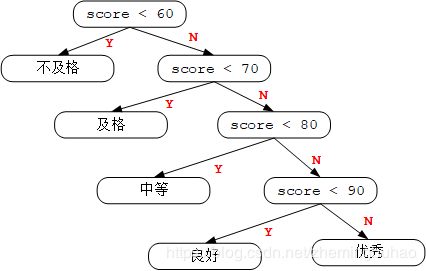
  那么根据上面表格中所显示的比例，将上面的程序的分支简单的修改一下，将出现频繁的分支往前面移动，出现不多的往后面移动，那么可以将上面的图可以修改为下图这样。

图1.1 修改和的成绩分布示意图

  
  那么有100个学生的话程序总共需要判断的次数为：

5 * 3 + 15 * 3 + 40 * 2 + 30 * 2 + 10 * 2 = 220 (次)

  
  明显的，判断的次数有明显的提升，那么上面修改后的图示就是霍夫曼树，也称为最优二叉树。

二、霍夫曼树

2.1、基本说明

  前面已经对霍夫曼树有了最简单的感觉，那么首先说明：

  路劲：从树中一个节点到另一个节点之间的分支构成两个节点之间的路径
  路劲长度：路劲上分支的数目
  带权路劲长度：从该节点到根节点之间的路劲长度与节点上权的乘积
  树的带权路劲长度：树中所有叶子节点的带权路劲长度之和，通常记为 ：$WPL={\sum }_{i=0}^n{w}_i{l}_i$

  假设有 $n$ 个权值 {$w_1$，$w_2$，…，$w_n$} ，试构造一个有 $n$ 个叶子节点的二叉树，每个叶子节点的权为 $w_i$ ，则其中带权路劲长度 $WPL$ 最小的二叉树称做最优二叉树或霍夫量树。

  所以说，上面提到的两种风格的树的形状，其进行 if 判断的次数，即为其对应的$WPL$，明显地第二种形状的树其$WPL$最小。

2.2、构建霍夫曼树

  既然霍夫曼树这么好，那么应该怎么构建这个霍夫曼树呢。霍夫曼最早给出了一个带有一般规律的算法，一般称为霍夫曼算法。描述如下：

  1、根据给定的 $n$ 个权值{$w_1$，$w_2$，…，$w_n$} 构成 $n$ 个二叉树的集合 $F$ ={$T_1$，$T_2$，…，$T_n$}， 其中每个二叉树 T，中只有一个带权为 $w_i$ 的根结点，其左右子树均为空
  2、在 F 中选取两个根结点的权值最小的树作为左右子树构造一个新的二叉树， 置新的二叉树的根结点的权值为其左右子树上根结点的权值之和
  3、在 F 中删除这两个树，同时将新得到的二叉树加入 F 中
  4、重复 2、3 步骤，直到 F 只含一个树为止，这个树便是霍夫曼树

（以上摘自《大话数据结构》P145）

  
  看完上面的总觉得可以了，但是大脑却一个劲的说不行，那我们用下面的一组图图来简单的描述一下上面的总结。

  假设有一个五二叉树在 A、B、C、D、E 构成的森林，权值分别为在 5、15、40、30、10 ，用这个创建一个霍夫曼树。

图2.1 二叉树集合示意图

  
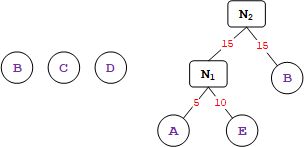
  1、取上面二叉树集合中两个权值最小的叶子节点组成一个新的二叉树，并且将权值最小的节点最为新二叉树（下图中节点 $N_1$ ）的左孩子。也就是节点 A （权值为 5 ）为新节点的左孩子，节点 E （权值为 10 ）为新节点的右孩子。新节点的权值则为两个孩子的权值的和（ 10+5 ），如下图所示。

图2.2 组建新节点示意图

  
  2、用 $N_1$ 替换节点 A 和节点 E ，为了统一插入，将新节点 $N_1$ 插入到集合的前面，如下图所示。

图2.3 二叉树集合分布示意图

  
  3、重复上面步骤2，再在集合中取一个权值最小的节点 B （权值为 15 ）与新节点 $N_1$ 组成新的节点 $N_2$ （权值为 15+15 ），如下图所示。

图2.4 组建新节点示意图

  
  4、将新节点 $N_2$ 替换节点 $N_1$ 与节点 B ，此时集合中还存在三个二叉树。分别为 {$N_2$、C、D}。
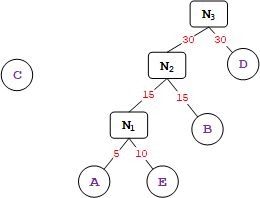
  5、重复上面步骤2，再在集合中取一个权值最小的节点 D （权值为 30 ）与新节点 $N_2$ 组成新的节点 $N_3$ （权值为 30+30 ），如下图所示。

图2.5 二叉树组建示意图

  
  6、将新节点 $N_3$ 替换节点 $N_2$ 与节点 D，此时集合中还存在两个二叉树。分别为 {$N_2$ 、C}。
  7、重复上面步骤2，再在集合中取一个权值最小的节点 C（权值为 40）与新节点 $N_3$ 组成新的节点 $N_4$ ，因为节点 C 的权值（ 40）小于节点 $N_3$ 的权值（ 60 ），所以节点 $N_3$ 为新节点 $N_4$ 的右孩子。新节点 $N_4$ 的权值为 40+60 ，如下图所示。

图2.6 霍夫曼树示意图

  
  8、此时集合中就剩下一各二叉树 $N_4$ 了，所以，霍夫曼树的创建完成了。

  此时，可以计算出来此二叉树的 $WPL$ ：

40 * 1 + 30 * 2 + 15 * 3 + 10 * 4 + 5 * 4 = 205   

  显然此时得到的值为 $WPL$ = 205，比之前我们自行做修改的二叉树的还要小，显然此时构造出来的二叉树才是最优的霍夫曼树。

2.3、霍夫曼树的存储结构

  根据上面的描述，如果树的集合中有 $n$ 个节点，那么我就需要 $2n-1$ 个空间用来保存创建的霍夫曼树中各个节点的信息。也就是需要创建一个数组 huffmanTree[$2n-1$]用来保存霍夫曼树，数组的元素的节点结构如下所示。

图2.7 霍夫曼树存储结构示意图

  其中：
    weight：权值域，保存该节点的权值
    lchild：指针域，节点的左孩子节点在数组中的下标
    rchild：指针域，节点的右孩子节点在数组中的下标
    parent：指针域，节点的双亲节点在数组中的下标

三、霍夫曼树的应用 — 霍夫曼编码

3.1、概述

  霍夫曼树的研究是为了当时在进行远距离数据传输的的最优化的问题，并且在现如今庞大的信息面前，数据的压缩显的尤为主要。而霍夫曼编码是首个使用的压缩编码方案。首先我们了解几个简单的概念。

  编  码：给每个对象标记一个二进制位串来表示一组对象，比如ASCII，指令系统等
  定长编码：表示一组对象的二进制位串的长度相等
  变长编码：表示一组对象的二进制位串的长度不相等，可以根据整体出现的频率来调节
  前缀编码：一组编码中任一编码都不是其他任何一个编码的前缀

  前缀编码保证了在解码时不会出现歧义，而霍夫曼编码就是一种前缀编码。

   比如一组字符串 “hello world”，如果采用ASCII进行编码，那么既可以表示为下表这样（包含空格）：

表3.1 字符串的ASCII表示表

字符串	h	e	l	l	o	(空格)	w	o	r	l	d
十六进制表示	0x68	0x65	0x6C	0x6C	0x6F	0x20	0x77	0x6F	0x72	0x6C	0x64
二进制表示	0110 1000	0110 0101	0110 1100	0110 1100	0110 1111	0010 0000	0111 0111	0110 1111	0111 0010	0110 1100	0110 0100

   显然，想要保存或者传输这么一个字符串的话，至少需要 12 个字节（字符串的结束符’\0’），也就是需要 12*8 个 bit 来保存或者传输。

   那么既然提到了霍夫曼编码，那么肯定霍夫曼编码可以解决这个占用多、效率低的问题了。

   首先各个字母出现的次数可以理解为其权值，所以上述字符串中各个字母的权值可以表示为下面这样。

表3.2 字母权值显示表

字符串	h	e	l	o	（空格）	w	r	d
权 值	1	1	3	2	1	1	1	1

   然后根据前面描述的创建霍夫曼树的步骤（点我查看构造霍夫曼树的详情），我们可以创建出来字符串 “hello world” 的最优的霍夫曼树，如下图左边所示。

图3.1 霍夫曼树示意图

  
   然后在上图左边所示的霍夫曼树中，将左分支上的原本表示权值的数值修改为表示路径的 0 ，将右分支上原本表示权值的数据修改成表示路径的 1，那么现实效果可以如上图右边所示。

表3.3 字母霍夫曼编码显示表

字符串	h	e	l	l	o	(空格)	w	o	r	l	d
霍夫曼编码	1111 110	1111 111	0	0	10	110	1111 10	10	1111 0	0	1110

   由此可见，数据的存储或者传输的空间大大的缩小，那么随着字符的增加和多自负权重的不同，这种压缩会更加的显示出其优势。

3.2、霍夫曼编码的代码实现

   那么根据上面的描述，霍夫曼树、霍夫曼编码的创建的实现代码可以如下编写。

/**
 *  功  能：
 *      创建一个霍夫曼树
 *  参  数：
 *      weight ：保存权值的数组
 *      num    ：权值数组的长度，也就是权值的个数 
 *  返回值：
 *      成功 ：创建成功的霍夫曼树的首地址
 *      失败 ：NULL
 **/
huffmanTree *Create_huffmanTree(unsigned int *weight, unsigned int num)
{
    huffmanTree *hTree = NULL;
    if (weight == NULL || num <= 1) // 如果只有一个编码就相当于0
        goto END;

    hTree = (huffmanTree *)malloc((2 * num - 1 + 1) * sizeof(htNode)); // 0号下标预留。用来表示初始化的状态，所以要在原来的基础上加1
    if (hTree == NULL)
        goto END;

    // 初始化哈夫曼树中的所有结点，均初始化为0
    memset(hTree, 0, (2 * num - 1 + 1) * sizeof(htNode));
    // 将权值赋值成传入的权值，并且从数组的第二个位置开始，i=1
    for (unsigned int i = 1; i <= num; i++)
        (hTree + i)->weight = *(weight + i - 1);

    // 构建哈夫曼树，将新创建的节点在原本节点的后边，从num+1开始
    for (unsigned int offset = num + 1; offset < 2 * num; offset++)
    {
        unsigned int index1, index2;
        select_minimum_index(hTree, offset - 1, &index1, &index2); // 获取权值最小的节点的下标

        // printf("index1 = %d, index2 = %d, hTree[1] = %d, hTree[2] = %d\n",
        //        index1, index2, hTree[index1].weight, hTree[index2].weight);

        (hTree + offset)->weight = (hTree + index1)->weight +
                                   (hTree + index2)->weight; // 将权值最小的两个节点的权值相加醉成新节点的权值
        (hTree + index1)->parent = offset;                   // 权值最小的节点的双亲结点为此新节点
        (hTree + index2)->parent = offset;                   // 值次小的节点的双亲结点为此新节点
        (hTree + offset)->lchild = index1;                   // 此新节点的左孩子为权值最小的节点
        (hTree + offset)->rchild = index2;                   // 此新节点的右孩子为权值次小的节点
    }

END:
    return hTree;
}

/**
 *  功  能：
 *       查询/计算在特定霍夫曼树下的对应圈权值的霍夫曼编码
 *  参  数：
 *      htree ：参考的霍夫曼树
 *      nums  ：原本权值的个数
 *      weight：权值
 *  返回值：
 *      成功：返回权值weight对应的编码
 *      失败：NULL
 **/
huffmanCode *Create_HuffmanCode_One(huffmanTree *htree, unsigned int nums, unsigned int weight)
{
    huffmanCode *hCode = NULL, *tmpCode = NULL;
    unsigned int i = 0, index = 0, parent = 0;

    if (htree == NULL || weight < 1)
        goto END;

    // 找到权值匹配的数组的下标
    while (htree[i].weight != weight && i <= nums)
        i++;
    if (i > nums) // 如果成立，额说明没有找到对应的权值，是为假权值
        goto END;

    tmpCode = (char *)malloc(sizeof(char) * nums);
    if (tmpCode == NULL)
        goto END;

    memset(tmpCode, 0, sizeof(char) * nums);
    // 霍夫曼编码的起始点，一般情况来说，最长的编码的长度为权值个数-1
    index = nums - 1;
    //从叶子到根结点求编码
    parent = (htree + i)->parent;
    while (parent != 0)
    {
        if ((htree + parent)->lchild == (unsigned int)i) //从右到左的顺序编码入数组内
            tmpCode[--index] = '0';                      //左分支标0
        else
            tmpCode[--index] = '1'; //右分支标1

        i = parent;
        parent = (htree + parent)->parent; //由双亲节点向霍夫曼树的根节点移动
    }

    hCode = (char *)malloc((nums - index) * sizeof(char)); //字符串，需要以'\0'为结束
    if (hCode == NULL)
        goto END;

    memset(hCode, 0, (nums - index) * sizeof(char));
    strcpy(hCode, &tmpCode[index]);

END:
    if (tmpCode != NULL)
        free(tmpCode);
    tmpCode = NULL;

    return hCode;
}

/**
 *  功  能：
 *      霍夫曼树的数组权值最小两个节点的下标
 *  参  数：
 *      htree  ：输入，霍夫曼树
 *      num    ：输入，霍夫曼树数组中有效节点的个数
 *      index1 ：输出，权值最小的节点的下标
 *      index2 ：输出，权值次小的节点的下标
 *  返回值：
 *      无
 **/
static void select_minimum_index(huffmanTree *htree, unsigned int num, unsigned int *index1, unsigned int *index2)
{
    unsigned int i = 1;
    // 记录最小权值所在的下标
    unsigned int indexMin;
    if (htree == NULL || index1 == NULL || index2 == NULL)
        goto END;

    // 遍历目前全部节点，找出最前面第一个没有被构建的节点
    while (i <= num && (htree + i)->parent != 0)
        i++;

    indexMin = i;

    //继续遍历全部结点，找出权值最小的单节点
    while (i <= num)
    {
        // 如果节点没有被构建，并且此节点的的权值比 下标为目前记录的下标的节点的权值小
        if ((htree + i)->parent == 0 && (htree + i)->weight < (htree + indexMin)->weight)
            indexMin = i; // 找到了最小权值的节点，下标为i
        i++;
    }
    *index1 = indexMin; // 最小的节点已经找到了，下标为 indexMin

    // 开始查找次小权值的下标
    i = 1;
    while (i <= num)
    {
        // 找出下一个没有被构建的节点，且没有被 index1 指向
        if ((htree + i)->parent == 0 && i != (*index1))
            break;
        i++;
    }
    indexMin = i;

    // 继续遍历全部结点，找到权值次小的那一个
    i = 1;
    while (i <= num)
    {
        if ((htree + i)->parent == 0 && i != (*index1))
        {
            // 如果此结点的权值比 indexMin 位置的节点的权值小
            if ((htree + i)->weight < (htree + indexMin)->weight)
                indexMin = i;
        }
        i++;
    }
    // 次小的节点已经找到了，下标为 indexMin
    *index2 = indexMin;

END:
    return;
}

3.3、测试案例及其运行效果

   测试案例就是主函数实现的代码，主要代码如下。

#include "../src/huffman/huffman.h"
#include 
#include 
#include 

int main(int argc, const char *argv[])
{
    int ret = 0;
    char chars[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G', '\0'};
    unsigned int weight[] = {5, 7, 2, 4, 1, 9, 8};
    unsigned char length = sizeof(weight) / sizeof(int);

    /* 根据已知的权重进行编码，解码 */
    // 创建霍夫曼树
    huffmanTree *htree = fhuffmanTree.buildHTree(weight, length);
    // 打印输出霍夫曼树的关系表格
    fhuffmanTree.printHTree(htree, 2 * length);
    // 创建霍夫曼编码
    huffmanCode **hcode = fhuffmanTree.getHCode(htree, length);
    // 打印输出霍夫曼编码
    fhuffmanTree.printHCode(hcode);

    /* 根据已知的字符串进行编码 */
    char *string = (char *)"ADZFBCD";
    char *stringCode = NULL;
    fhuffmanTree.toHcode(hcode, chars, length, string, &stringCode);
    printf("The input string '%s' Encoded by Huffman is : \n\n\t%s\n\n", string, stringCode);

    /* 根据已知的字符串进行解码 */
    char *coding = (char *)"110001101110001001";
    char *codeString = NULL;
    fhuffmanTree.toString(htree, chars, length, coding, &codeString);
    printf("The input coding '%s' Decoded by Huffman is : \n\n\t%s\n\n", coding, codeString);

    fhuffmanTree.destoryHTree(htree);
    fhuffmanTree.destoryHCode(hcode);

    free(stringCode);
    stringCode = NULL;
    free(codeString);
    codeString = NULL;

    printf("\nsystem exited with return code %d\n", ret);

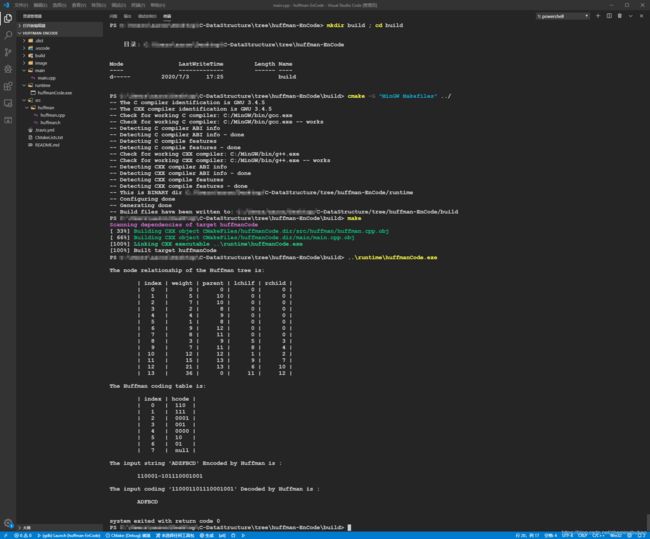
    return ret;
}

   工程管理使用常见的 cmake 进行管理，项目工程结构如下图左上角所示，比较清楚不再赘述。
   项目创建、编译、运行在下图中均已经显示明白，不再赘述。
   具体的测试效果如下图所示。

图3.2 霍夫曼运行效果示意图

  
  好啦，废话不多说，总结写作不易，如果你喜欢这篇文章或者对你有用，请动动你发财的小手手帮忙点个赞，当然 关注一波 那就更好了，好啦，就到这儿了，么么哒(* ￣3)(ε￣ *)。

上一篇：数据结构（十九） – C语言版 – 树 - 树、森林、二叉树的江湖爱恨情仇、相互转换
下一篇：数据结构（廿一） – C语言版 – 图 - 图的基本概念