python算法——大O表示法
大O表示法
大O表示法的样子为 O(操作数)
大O表示法指出了算法的速度有多快
它的好处在于,当我们引用别人的算法时,了解了它的大O表示法会对我们大有益处。(一般情况下用处不大,但了解总是好的)
不同的大O运行时间
当要找出一堆数中最大的数时:
1.遍历所有的数
2.找出最大数
def Max(n):
for k in n:
max_number = 0
if max_number < k:
max_number = k
return max_number
print(Max([1, 3, 5, 7, 9]))
这里需要把列表所有的元素都检查一遍,因此运行时间也就是列表中所有元素检查一遍的时间。用大O表示法表示为O(n)
当把一堆数按从小到大排列时:
1.找出最小的数,把它加入新列表并从原列表中删除
2.有多少数执行多少次
def find_min(n):
minest = n[0]
minest_index = 0
for i in range(1, len(n)):
if minest > n[i]:
minest = n[i]
minest_index = i
return minest_index
def array(n):
NewArr = []
for i in range(len(n)):
minest = find_min(n)
NewArr.append(n.pop(minest))
return NewArr
print(array([9, 7, 5, 3, 1]))
这里每次都需要遍历所有数,遍历的次数为元素的数量。大O表示法为O(n*n),即O(n^2)
*注:即使下一次需要遍历的数量比上一次少一,但它还是n。
大O表示法中的常量
一些常见的大O表示法
基于每秒执行10次计算的,但计算机运行速度并不是这样。只是为了有个大概的计量,便于了解之间的差别。
常量c
比较一下下面两个打印列表的函数:
1.打印一个列表
def print_number1(list):
for k in list:
print(k)
print_number1([1, 3, 5, 7, 9])
2.打印一个列表,每打印一个数字休眠1秒
from time import sleep
def print_number2(list):
for k in list:
print(k)
sleep(1)
print_number2([1, 3, 5, 7, 9])
可以看出两个函数的大O表示法都为 O(n),因为它们都遍历了一个列表。但是可以明显感觉到print_number1的运行速度要比print_number2快许多。因为它没有每次运行后休眠1秒。但从大O表示法来看二者的运行速度是一样的,但print_number1的运行速度要快。在大O表示法中n指的其实是c*n。
这个c指的是算法所需的固定时间,被称为常量。print_number1指的是 10毫秒*n 。
print_number2指的是 1秒*n。
通常这个常量是不被考虑进来的,因为大O运行时间不同,这个常量无关紧要。
举个例子:
用上图的简单查找和二分查找来说。
设简单查找的运行常量为10毫秒,二分查找的运行常量为10秒。
当元素数量很多(10亿)的时候
二者的运行时间为
简单查找:10毫秒*10亿=1亿秒
二分查找:10秒*log(10亿)=300秒
很明显二分查找要比简单查找快的多,所以常量基本没什么影响。
但有时候常量有的影响可能会很大,比如说上例中打印列表的函数。print_number1的常量比print_number2小,但它们的运行时间都为O(n)
所以print_number1的运行速度更快。实际上print_number1的运行速度确实要快。相对于糟糕情况,遇上平均情况的可能性要大的多。
平均情况与最糟情况
这里要涉及到快速排序
在快速排序中,性能的高低取决于所选的,基准值。
假如你每次都将第一个元素作为基准值,且元素是有序的,由于快速排序不检查数组是否有序,因此它依旧会按照程序运行
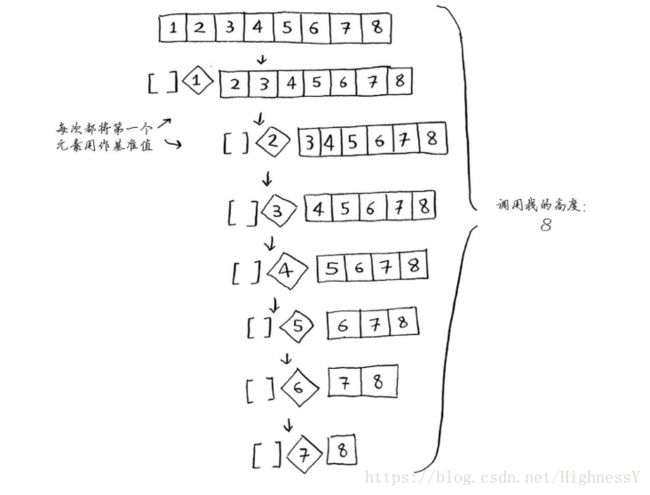
注意这里数列没有被分为两半,其中一个子序列总是为空。导致了调用栈很长。
如果每次的基准值都是中间元素呢
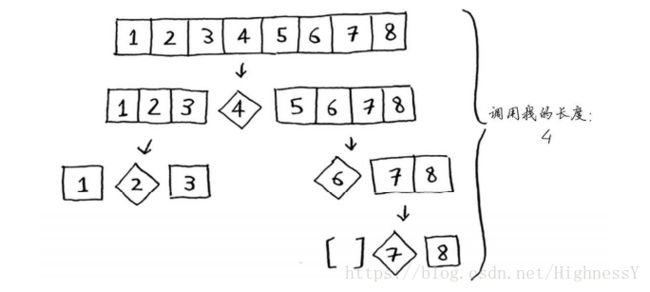
这里调用栈短很多,因为每次都将数组分为两半,很快就到达了基线条件。因此调用栈短很多。
以上两种情况就是最糟情况与最佳情况。
最糟情况下:栈的长度为O(n),每层都涉及O(n)个元素。所以运行时间为O(n*n)
最佳情况下:栈的长度为O(logn),每层涉及O(n)个元素。所以运行时间为O(logn*n)
这里的最佳情况也就是平均情况。只要你每次选基准值都是随机的,快速排序的运行时间都为O(logn*n)。