2020年百度之星·程序设计大赛-初赛三 补题/解题
Title
- Discount
- 题解
- Game
- 题解
- Permutation
- 题解
- Intersection
- 题解
- Chess
- Ant
- Fight
- Graph
Discount
Problem Description
学皇来到了一个餐馆吃饭。他觉得这家餐馆很好吃,于是就想办个会员。
一共有 n 种会员充值卡套餐,假设学皇这餐饭的消费为 a 元,选择第 i 种套餐,需要充值 b[i]∗a 的钱,这次吃饭可以打 c[i]×10 折,由充值的钱支付(即这次吃饭只需要从充值金额中扣除 a×c[i] 元)。以后用剩余的充值的钱吃饭不再打折。
请问学皇应该选择哪个套餐(必须选择恰好一个套餐),使得优惠的比例最大?
优惠比例的定义是把充的钱用完以后,(本来应该付的钱 - 实际付的钱) / 本来应该付的钱。在这个题目里,实际付的钱就是这次充值的花费。
Input
第一行一个整数 test(1≤test≤100) 表示数据组数。
对于每组数据,第一行一个正整数 n(1≤n≤100) 表示套餐的数目。
接下来 n 行,每行一个正整数 b[i] (1≤b[i]≤100) 和一个小数 c[i] (0≤c[i]≤1,c[i] 最多包含两位小数)。
Output
对于每组数据,输出一个五位小数表示最大的优惠比例。如果小数点后超过五位,四舍五入到五位。
Sample Input
1
2
2 0.5
3 0.1
Sample Output
0.23077
样例解释
对于第一种套餐,优惠比例为 0.5a / (2a + 0.5a) = 0.2;
对于第二种套餐,优惠比例为 0.9a / (3a + 0.9a) = 9 / 39;
题解
#include
#include
int b[105];
double c[105];
int main()
{
int t,n,i;
double ans,sum;
scanf("%d",&t);
while(t--)
{
ans=0;
scanf("%d",&n);
for(i=0;i Game
Problem Description
Alice 和 Bob 在玩游戏。
桌面上有两堆金币,少的那堆有 x 个金币,多的那堆有 2x 个金币。
假设金币可以被无限细分。Alice 和 Bob 事先都不知道 x 是几,但是他们都知道 x 是一个 (0,1] 之间均匀分布的随机实数。
Alice 会等概率的被分配到其中的一堆金币,Bob 会得到另一堆。x 的值和两堆金币的分配是相互独立的。
拿到金币以后,Alice 会马上数清自己拿到多少金币。然后 Alice 可以选择是否和 Bob 那堆换。
给定 Alice 拿到的金币数目,请问 Alice 要不要交换,使得她期望能得到的金币数目更多?
如果交换期望得到的金币数目多于不交换期望得到的金币数目,输出交换,否则不交换。
Input
第一行一个正整数 test (1≤test≤200000) 表示数据组数。
接下来每行一个小数 p (0
Output
对于每组数据,输出 Yes 表示需要交换,输出 No 表示不要交换。
Sample Input
1
1.00000
Sample Output
Yes
题解
#include
#include
int b[105];
double c[105];
int main()
{
int t;
float p;
scanf("%d",&t);
while(t--)
{
scanf("%f",&p);
if(p>1.0)
printf("No\n");
else
printf("Yes\n");
}
return 0;
}
Permutation
Problem Description
一开始有 n 个数,他们按 1…n 的顺序排列,要求交换最多 m 对数字(同一个数字可以参与多次交换),使得逆序对数目最大。
对于一个序列 A,如果存在正整数 i,j 使得 1≤i
Input
第一行一个正整数 test (1≤test≤100000) 表示数据组数。
对于每组数据,一行两个整数 n,m (1≤n≤1000000,0≤m≤1000000) 表示数字个数和最多可以交换的数字对数。
Output
对于每组数据,一行一个整数表示答案。
Sample Input
6
1 1
2 0
2 1
3 1
4 1
4 2
Sample Output
0
0
1
3
5
6
题解
#include
#include
#include
#include
#define ll long long
using namespace std;
int main()
{
ll t,n,m;
scanf("%lld",&t);
while(t--)
{
scanf("%lld%lld",&n,&m);
ll ans=0;
if(n==1||m==0)
ans=0;
else if(m>=n/2)
{
ans=n*(n-1)/2;
}
else
{
ll min=n-2*m;
ans=(min+n-1)*(n-min)/2;
}
printf("%lld\n",ans);
}
return 0;
}
Intersection
Problem Description
Mr. Left 来到了一个路口,这个路口只能右转,并且都是两车道。
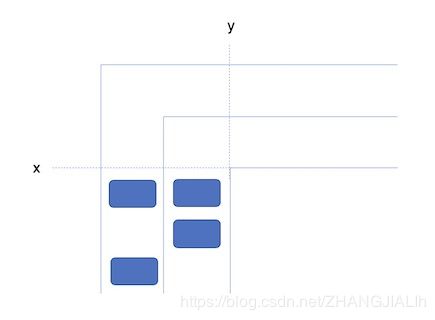
现在在南北向车道上有 n 辆车,他们都在线 x 南边,这些车想要通过这个路口,到东边去,具体地说,他们要开到线 y 东边。
一辆车一个时刻可以从东南西北中选一个方向移动一个位置,或者呆在原地不动。
同一时刻同一位置不能有超过一辆车。车不能开到路外面。
在任意时刻,所有车都同时移动。两辆相邻的车不能都移动到对方的格子上。在此基础上,只要所有车移动后不存在两辆车处于同一位置,移动就合法。
问最少要多少时间,这些车才可以都开到东边?
Input
第一行一个整数 test (1≤test≤10)。
对于每组数据,第一行一个整数 n (1≤n≤100000),表示车辆数目。
接下来 n 行,每行两个整数 x,y 表示车的位置,其中 x 表示车道 id( x=1 表示右车道,x=2 表示左车道),y (1≤y≤100000) 表示车在路口前第几个位置。
数据保证没有两辆车初始在同一位置。
Output
对于每组数据,一行一个整数表示答案。
Sample Input
2
2
1 1
2 1
2
1 2
2 1
Sample Output
3
4
样例解释
第一组
time 0
…
…
CC
…
time 1
…
CC…
…
…
time2
…
.CC.
…
…
time3
…
…CC
…
…
第二组
time 0
…
…
C.
.C
time 1
…
C…
.C
…
time2
C…
.C…
…
…
time3
.C…
…C.
…
…
time4
…C.
…C
…
…
题解
Chess
Problem Description
你现在有一个棋盘,上面有 n 个格子,格子从左往右,1,…,n 进行标号。你可以在棋盘上放置恰好 m 个传送器,并且对于每个传送器设置传送位置。
传送位置需满足:对于在 i 号格子上的传送器,传送目标位置 j 满足 j
现在有一名玩家,拿着一枚 1,…,11 的骰子(骰子每次等概率地投出 1 到 11 中的一个数字),从位置 1 开始,用骰子决定前进步数,即如果当前在位置 y 且投出数字 x,那棋子将会跳到位置 y+x。如果棋子跳到棋盘外的位置(x+y>n),玩家失败。如果位置 y+x上恰好有个传送器,那玩家的棋子立刻会被传送到传送器目标位置。如果传送器目标位置有另一个传送器,玩家的棋子会沿着另一个传送器继续传送。这个过程持续若干次,直到目标位置没有传送器为止。
如果玩家棋子可以到达点 n 且不被传送到别的地方(意味着位置 n 没有传送器),则玩家获胜。
问现在有多少种不同的放置传送器的方法,使得玩家有可能获胜。如果摆放传送器的格子不同或者某个格子上的传送器传送的位置不同则视为不同的方案。
每个格子最多放置一个传送器。
Input
第一行一个正整数 test (1≤test≤20) 表示数据组数。
对于每组数据,第一行两个整数 n,m (1≤n≤1000,0≤m≤1000) 表示格点数和传送器数。
Output
对于每组数据,一行一个整数表示答案模 109+7。如果无解(没有任何获胜的方案),输出 −1。
Sample Input
1
12 10
Sample Output
3628800
Ant
Problem Description
有一棵 n 个节点的石榴树,点的下标为 1…n,下标为 m 的节点上有一颗石榴。石榴树有 2n−2 条有向边,每条有向边都连接两个不同的节点,不存在完全相同的两条有向边,且如果从节点 a 到节点 b 的有向边存在,反过来从节点 b 到节点 a 的有向边也必定存在。从任意一个节点都能(经过这些有向边中的若干条)到达任意一个其它节点。
现在有两只小蚂蚁去找石榴。
两只小蚂蚁都从 1 号点出发,第一只蚂蚁先走。它每次会从它当前所在的节点出发的没有走过的有向边中等概率地选择一条走(注意从 a 到 b 和从 b 到 a 是两条不同的有向边),并且在这条有向边上留下信息素。如果蚂蚁找到了石榴,或者无路可走了,它就会停下来。
第一只蚂蚁停下来以后第二只蚂蚁走,它每次从它当前所在的节点出发的有第一只蚂蚁留下的信息素且自己没走过的有向边中等概率地选择一条走。如果第二只蚂蚁找到了石榴,或者它无路可走了,它就会停下来。
如果第二只蚂蚁沿着从 1 到 m 的最短路找到了石榴,就说它成功了。请问对于第一只蚂蚁,使得第二只蚂蚁成功率大于等于 1/2 的概率是多少?
Input
第一行一个正整数 test (1≤test≤100) 表示数据组数。
对于每组数据,第一行两个正整数 n,m (1≤n≤100000,1≤m≤n) 分别表示点数和石榴在哪里。
接下来 n−1 行描述 2n−2 条有向边,每行两个整数 x,y 代表从 x 到 y 和从 y 到 x 各有一条有向边。
数据保证读入是一棵合法的石榴树,数据保证树是这样随机生成的:
for (int i = 1; i <= n; i++)
a[i] = i;
random_shuffle(a + 1, a + n + 1);
for (int i = 2; i <= n; i++)
连接编号为 a[i] 和 a[j] 的点,其中 j 为 {1, ..., i-1} 中一个随机的整数。每次随机相互独立。
(实际上每次随机使用了C++自带的随机函数。)
Output
对于每组数据,一行一个数表示答案。由于答案 A/B 中的 AB 可能很大,请输出 A/Bmod(109+7)。假设 A/B 为最简分数,A/Bmod(109+7)=A×B−1mod(109+7),B−1 为满足 B−1×Bmod(109+7)=1 的整数。
Sample Input
3
1 1
4 2
1 2
1 3
1 4
5 4
1 2
1 3
3 4
3 5
Sample Output
1
666666672
416666670
Fight
Problem Description
Mr Left,Mr Mid,Mr Right 正在玩游戏。他们初始都有 1000 血,Mr Left,Mr Mid,Mr Right 的攻击力分别为 x,y,z。
对于每一轮,假设仍然剩下至少两个人的血量大于 0,那么选出两个血量大于 0 的人对打,他们的血量分别扣除和他们对打的另一个人的攻击力。
当有至少两个人的血量小于等于 0 时,游戏结束。
请问在最优情况下,这个游戏最少多少轮结束?
Input
第一行一个正整数 test (1≤test≤100) 表示数据组数。
接下来 test 行,每行三个正整数 x,y,z (1≤x,y,z≤1000) 表示 Mr Left, Mr Mid, Mr Right的攻击力。
Output
对于每组数据,一行一个整数表示答案。
Sample Input
2
1 1 1
1 2 3
Sample Output
1000
666
Graph
Problem Description
给你一张 n 个点 m 条边的无向连通图,现在你要将数字 1,…,m 填到边上作为边权,每个数字能出现一次且仅能出现一次。
问有多少种方法使得图上没有一个简单环的边权和为偶数。两种方案会被视为不同方案当且仅当存在至少一条边在两种方案中的边权不同。
简单环是不经过重复点的环。
Input
第一行一个正整数 test (1≤test≤5) 表示数据组数。
对于每组数据,第一行两个整数 n,m (1≤n,m≤100000) 表示图的点数和边数。
接下来 m 行每行两个整数 u,v 表示图上的点 u 和点 v 之间有一条无向边。
点的编号为 1,…,n。
数据保证没有自环和重边。
Output
对于每组数据,一行一个整数表示答案模 998244353。
Sample Input
2
3 2
1 2
2 3
4 4
1 2
2 3
3 4
4 1
Sample Output
2
0