图论(kuangbin)题解

最近看到队中的大佬可怕的做题量,弱鸡感受到了发自内心的恐惧,于是我这个弱鸡决定加强自己的日常训练(熬夜就熬夜吧,少年不熬夜,老大徒伤悲(雾))

随时扩充

强连通相关

POJ 1236 Network of Schools(板子)

转化一下就是第一问求缩点之后入度为零的点的个数第二问求(入度为零和出度为零的最值)
因为本人 菜鸡并不擅长压行,所以他们50行可以写完的代码,我要写100+行(留下没有尊严的泪水)

ACcode:

#include 
#include 
#include 
#include 
#define MAX 110
using namespace std;
struct node{
	int to,nxt;
}edge[MAX*MAX];
int n;
int head[MAX];
int len;

void addedge(int from,int to) 
{
	edge[len]={to,head[from]};
	head[from]=len++;
}//链式向前星 

stack<int> st;
int low[MAX];
int dfn[MAX];
int vis[MAX];
int book[MAX];
int num;
int cnt;

void tarjan(int now)
{
	low[now]=dfn[now]=cnt++;
	vis[now]=1;
	st.push(now);
	for(int i=head[now];i!=-1;i=edge[i].nxt)
	{
		int to=edge[i].to;
		if(dfn[to]==0)
		{
			tarjan(to);
			low[now]=min(low[now],low[to]);
		}
		else if(vis[to]==1)
		{
			low[now]=min(low[now],dfn[to]);
		}
	}
	
	if(low[now]==dfn[now])
	{
		num++;
		while(1)
		{
			int t=st.top();
			st.pop();
			vis[t]=0;
			book[t]=num;
			if(t==now)
			break;
		}
	}
	
}//tarjan 



void init()
{
	memset(head,-1,sizeof(head));
	cnt=1;
	num=0;
	len=0;
}

int main()
{
	init();
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		int a;
		while(cin>>a,a!=0)
			addedge(i,a);
	}
	for(int i=1;i<=n;i++)
	{
		if(dfn[i]==0)
		tarjan(i);
	}
	int in[MAX]={0};
	int out[MAX]={0};
	for(int i=1;i<=n;i++)
	{
		for(int j=head[i];j!=-1;j=edge[j].nxt)
		{
			int to=edge[j].to;
			if(book[to]!=book[i])
			{
				in[book[to]]++;
				out[book[i]]++;
			}
			
		}
	}
	int ans1=0;
	int ans2=0;
	for(int i=1;i<=num;i++)
	{
		if(in[i]==0)
		ans1++;
		if(out[i]==0)
		ans2++;
	}
	cout<<ans1<<endl;
	cout<<(num==1? 0:max(ans1,ans2));
	return 0;
}

Network UVA - 315(割点板子)

一道裸的求割点的题,就是UVA不太行,一道题要判14+mins…跪了

ACcode:

#include 
#include 
#include 
#include 
#define MAX 110
using namespace std;
struct node{
	int to,nxt;
}edge[MAX*MAX];

int head[MAX];
int len=0;

void addedge(int from,int to)
{
	edge[len]={to,head[from]};
	head[from]=len++;
}

int dfn[MAX];
int low[MAX];
int cnt;
int root;
int isit[MAX]; 
int n;

void tarjan(int now)
{
	dfn[now]=low[now]=cnt++;
	int child=0;
	for(int i=head[now];i!=-1;i=edge[i].nxt)
	{
		int to=edge[i].to;
		if(dfn[to]==0)
		{
			child++;
			tarjan(to);
			low[now]=min(low[now],low[to]);
			if(now==root&&child>=2)
			isit[now]=1;
			else if(now!=root&&dfn[now]<=low[to])
			isit[now]=1;
		}
		else
		{
			low[now]=min(low[now],dfn[to]);
		}
	}
}

void init()
{
	len=0;
	cnt=1;
	memset(head,-1,sizeof(head));
	memset(dfn,0,sizeof(dfn));
	memset(isit,0,sizeof(isit));
}

int main()
{
	while(cin>>n,n)
	{
		init();
		int i;
		while(cin>>i,i)
		{
			char k;
			while(k=getchar(),k!='\n')
			{
				int a;
				cin>>a;
				addedge(i,a);
				addedge(a,i);
			}
		}
		
		for(int i=1;i<=n;i++)
		{
			if(dfn[i]==0)
			{
				root=i;
				tarjan(i);
			}
		}
		int ans=0;
		for(int i=1;i<=n;i++)
		if(isit[i])
		ans++;
		cout<<ans<<endl;
	}
	
	return 0;
}
/*
5
5 1 2 3 4
0
6
2 1 3
5 4 6 2
0
0
*/

Ant Network LightOJ - 1308(割点+简单思维)

题意很简单,随意炸掉一个点,问最少建立几个出口能够让所有没有被炸掉的点都能到达出口,并输出方案的个数;

炸掉的点如果不是割点就一点意义都没有…所以一上来就可以确定这是一个割点题,剩下的讨论一下就好:

1. 如果图中没有割点,直接随意定两个出口就行–>直接输出2 (n-1)*n/2;
2. 如果图中有割点,我们就只需要考虑被割点分开的联通集就好,但刚开始这里考虑的不细致…以为是所有分量大小的乘积就是答案,但很显然不是,因为我们只会炸一个点,所以如果这个分量连接了两个以上的割点,我们是不需要在这个分量上建立出口的…考虑到这里这个题就可以秒了…

因为代码很水,就不贴代码了…

Network POJ - 3694(缩点+LCA)

太菜了(第一个不是板子的题就不会写…)
get:
通过本题学会了缩点的高端写法(tarjan套并查集法),对于有环图变树的理解更深了.更正了一个对割边的错误理解(一定是 不通过该边 无法访问到以前节点的边才叫"割边",所以一定要把来时的边跳过才行)

题意: 给你一个无向连通图,然后依次添Q条边,问你每添一条边"割边"(删掉会改变连通性的边)的个数.

显然面对1e5的点和1e3次查询,每次都跑tarjan是行不通的,所以这里优化的方案是在上一次的查询基础之上找到有几条边不再是割边了,减掉就好了.

这个题很容易想到缩点,因为无环图(本题是树)总是要比有环图清晰,好处理.
1.树上的所有边都是"割边"
2.在树上的两个点a和b之间添一条边,那么一定会成环,环上的边就不是"割边"了,而除去新添的那条边,剩下的边的组合就是a->b的路径,也十分好处理,可以通过LCA处理.
但是LCA有一个条件->我们要知道每个节点所处于的层次.可以先通过tarjan缩点,然后在通过BFS实现,但这太麻烦了,我们只需要对tarjan稍作修改,把dfn数组的含义调整为层数就好了.

ACcode

#include 
#include 
#include 
#include 
#define MAX 100010
using namespace std;
struct node{
	int to;
	int nxt;
}edge[MAX*4];
int pre[MAX];
int fa[MAX];

int ans;
int n,m;
int head[MAX];
int len=0;

void addedge(int from,int to)
{
	edge[len]={to,head[from]};
	head[from]=len++;
}

int find(int x)
{
	return (pre[x]==x? x:pre[x]=find(pre[x]));
}

void join(int a,int b)
{
	int fa=find(a);
	int fb=find(b);
	if(fa!=fb)
		pre[fa]=fb;
}

int dfn[MAX];
int low[MAX];
int vis[MAX];

void tarjan(int now,int last,int c)
{
	dfn[now]=low[now]=c;
	vis[now]=1;
	fa[now]=last;
	for(int i=head[now];i!=-1;i=edge[i].nxt)
	{
		int to=edge[i].to;
		if(to==last) continue;
		if(dfn[to]==0)
		{
			tarjan(to,now,c+1);
			low[now]=min(low[now],low[to]);
			if(dfn[now]<low[to])
				ans++;
			else
			join(now,to);
		}
		else if(vis[to]==1)
		low[now]=min(low[now],dfn[to]);
	}
	vis[now]=0;//退栈(妙啊)
}

void LCA(int a,int b)
{
	while(dfn[a]>dfn[b])
	{
		if(find(a)!=find(fa[a]))
		ans--;
		join(a,fa[a]);
		a=fa[a];
	}
	
	while(dfn[b]>dfn[a])
	{
		if(find(b)!=find(fa[b]))
		ans--;
		join(b,fa[b]);
		b=fa[b];
	}
	
	while(a!=b)
	{
		if(find(a)!=find(fa[a]))
		ans--;
		if(find(b)!=find(fa[b]))
		ans--;
		join(a,fa[a]);
		join(b,fa[b]);
		b=fa[b];
		a=fa[a];
	}
}

void init()
{
	len=0;
	ans=0;
	memset(head,-1,sizeof(head));
	memset(dfn,0,sizeof(vis));
	memset(fa,0,sizeof(fa));
	for(int i=1;i<MAX;i++)
	pre[i]=i;
}

int main()
{
	std::ios::sync_with_stdio(false);
	
	int p=1;
	while(cin>>n>>m,n||m)
	{
		init();
		for(int i=0;i<m;i++)
		{
			int a,b;
			cin>>a>>b;
			addedge(a,b);
			addedge(b,a);
		}
		tarjan(1,0,1);
		int q;
		cin>>q;
		cout<<"Case "<<p<<":"<<endl;
		p++;
		for(int i=1;i<=q;i++)
		{
			int a,b;
			cin>>a>>b;
			LCA(a,b);
			cout<<ans<<endl;
		}
		cout<<endl;
	}
	return 0;
}

(两点半了,溜了)

Redundant Paths POJ - 3177(简单缩点)

这道题和上一题很像,所以这题就小意思啦,唯一值得注意的是这个题可能有重边.
所以在判断反向边的时候要用

if(i==(last^1)) continue;

这样写要注意edge[]的下标从0开始,并且反向边和正向边要在一起建立.
此外就没有什么要注意的了
ACcode:

#include 
#include 
#include 
#define MAX 5050
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
struct node{
	int to,nxt;
}edge[MAX*4];
int n,m;
int head[MAX];
int fa[MAX];
int len;

void addedge(int from,int to)
{
	edge[len]={to,head[from]};
	head[from]=len++;
}

int find(int x)
{
	return (x==fa[x]? x:fa[x]=find(fa[x]));
}

void un(int a,int b)
{
	int f1=find(a);
	int f2=find(b);
	if(f1!=f2)
	fa[f1]=f2;
}

int vis[MAX];
int low[MAX];
int dfn[MAX];
int cnt;

void tarjan(int now,int last)
{
	low[now]=dfn[now]=cnt++;
	vis[now]=1;
	for(int i=head[now];i!=-1;i=edge[i].nxt)
	{
		int to=edge[i].to;
		if(i==(last^1)) continue;
		if(dfn[to]==0)
		{
			tarjan(to,i);
			low[now]=min(low[now],low[to]);
			if(dfn[now]<low[to]) continue;
			else
			un(now,to);
		}
		else if(vis[to]==1)
		low[now]=min(low[now],dfn[to]);
	}
	vis[now]=0;
}

void init()
{
	len=0;
	cnt=1;
	mem(head,-1);
	for(int i=1;i<MAX;i++)
	fa[i]=i;
}
int main()
{
	init();
	cin>>n>>m;
	for(int i=0;i<m;i++)
	{
		int a,b;
		cin>>a>>b;
		addedge(a,b);
		addedge(b,a);
	}
	tarjan(1,-1);
	int du[MAX]={0};
	for(int i=1;i<=n;i++)
	for(int j=head[i];j!=-1;j=edge[j].nxt)
	{
		if(find(i)!=find(edge[j].to))
		{
			du[find(i)]++;
		}
	}
	int ans=0;
	for(int i=1;i<=n;i++)
	if(du[i]==1)
	ans++;
	cout<<(ans+1)/2;
	return 0;
}
/*
8 9
1 2
1 3
1 8
2 4
2 5
3 6
3 7
8 4
2 5
*/

Warm up HDU - 4612(缩点+树的直径)

忘记清空deep数组了…不然就秒杀了…(还是太菜)

有了前两题的铺垫,这题放到这里就是送分鸭,太爽了
答案=桥的个数-树的直径

ACcode:

#include 
#include 
#include 
#include 
#define MAX 200020
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
struct T{
	int head[MAX];
	pair<int,int> edge[MAX*10];
	int cnt;
	
	void init()
	{
		cnt=0;
		mem(head,-1);
	}
	
	void addedge(int from,int to)
	{
		edge[cnt]=make_pair(to,head[from]);
		head[from]=cnt++;
	}
}mp1,mp2;

int n,m;
int fa[MAX];
int low[MAX];
int dfn[MAX];
int vis[MAX];
int len;
int book[MAX];
int deep[MAX];
int find(int x)
{
	return (fa[x]==x? x:fa[x]=find(fa[x]));
}

void un(int a,int b)
{
	int f1=find(a);int f2=find(b);
	if(f1!=f2) fa[f1]=f2;
}


void tarjan(int now,int last)
{
	low[now]=dfn[now]=len++;
	vis[now]=1;
	for(int i=mp1.head[now];i!=-1;i=mp1.edge[i].second)
	{
		int to=mp1.edge[i].first;
		if(i==(last^1)) continue;
		if(dfn[to]==0)
		{
			tarjan(to,i);
			low[now]=min(low[now],low[to]);
			if(low[to]>dfn[now]) continue;
			un(to,now);
		}
		else
			low[now]=min(low[now],dfn[to]);
	}
	vis[now]=0;
}

void init()
{
	len=1;
	mem(dfn,0);
	for(int i=1;i<MAX;i++)
	fa[i]=i;
	mem(deep,0);
	mp1.init();
	mp2.init();
}

void dfs(int now,int last)
{
	deep[now]=(last==-1? 1:deep[last]+1);
	for(int i=mp2.head[now];i!=-1;i=mp2.edge[i].second)
	{
		int to=mp2.edge[i].first;
		if(deep[to]==0)
		dfs(to,now);
	}
}


int main()
{
	while(scanf("%d%d",&n,&m),n||m)
	{
		init();
		int a,b;
		for(int i=0;i<m;i++)
		{
			scanf("%d%d",&a,&b);
			mp1.addedge(a,b);
			mp1.addedge(b,a);
		}
		tarjan(1,-1);
		int num=0;
		
		for(int i=1;i<=n;i++)
		if(fa[i]==i)
		book[i]=++num;//把根节点离散一下,方便处理 
		
		for(int i=1;i<=n;i++)
		{
			for(int j=mp1.head[i];j!=-1;j=mp1.edge[j].second)
			{
				int to=mp1.edge[j].first;
				int a=find(i);
				int b=find(to);
				if(a!=b)
				{
					mp2.addedge(book[a],book[b]);
					mp2.addedge(book[b],book[a]);
				}
			}
		}

		dfs(1,-1);
		int M_num=-1;
		for(int i=1;i<=num;i++)
		if(M_num<deep[i]) M_num=deep[i];
		for(int i=1;i<=num;i++)
		if(deep[i]==M_num)
		{
			mem(deep,0);
			dfs(i,-1);
			break;
		}
		M_num=-1;
		for(int i=1;i<=num;i++)
		if(M_num<deep[i]) M_num=deep[i];
		cout<<(num-M_num)<<endl;
	}
	return 0;
} 



/*
8 9
1 2
1 3
1 8
2 4
2 5
3 6
3 7
8 4
2 5

7 6
1 2
1 3
2 4
2 5
3 6
3 7
*/

我已经在尽力的压行了…但为什么他们能在80行内写完?(小小的眼睛里充满了 异或 疑惑)

Strongly connected HDU - 4635(简单缩点)

题意:给一个简单有向图如果是强连通图输出-1,否则输出在简单图的基础上,最多添几条边,保证它还是一个无向图.
思路很简单因为用稍稍推(cai)一下就知道当两个强连通分量的大小差距越大,边就越多,所以这个题就变得很简单了(但还是被坑了一发…)因为要找的被分割开的强连通分量必须入度为0或者出度为0…

ACcode:

#include 
#include 
#include 
#include 
#include  
#define ll long long
#define MAX 100010
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
struct node{
	int to,nxt;
}edge[MAX];

int head[MAX];
int cnt;
int n,m;
void addedge(int from,int to)
{
	edge[cnt]={to,head[from]};
	head[from]=cnt++;
}
stack<int> st; 
int dfn[MAX];
int low[MAX];
int vis[MAX];
int book[MAX];
int fa[MAX];
int in[MAX];
int out[MAX];
int num;
int len;

void tarjan(int now)
{
	low[now]=dfn[now]=len++;
	vis[now]=1;
	st.push(now);
	for(int i=head[now];i!=-1;i=edge[i].nxt)
	{
		int to=edge[i].to;
		if(dfn[to]==0)
		{
			tarjan(to);
			low[now]=min(low[now],low[to]);
		}
		else if(vis[to])
		{
			low[now]=min(low[now],dfn[to]);
		}
	}
	
	if(dfn[now]==low[now])
	{
		num++;
		while(1)
		{
			int t=st.top();
			st.pop();
			vis[t]=0;
			fa[t]=num;
			book[num]++;
			if(t==now)
			break;
		}
	}
	
}

void init()
{
	mem(head,-1);
	mem(dfn,0);
	mem(in,0);
	mem(out,0);
	cnt=0;
	len=1;
	num=0;
	mem(book,0);
	while(!st.empty())
	st.pop();
}

int main()
{
	int t;
	scanf("%d",&t);
	for(int q=1;q<=t;q++)
	{
		printf("Case %d: ",q);
		init();
		scanf("%d%d",&n,&m);
		int a,b;
		for(int i=0;i<m;i++)
		{
			scanf("%d%d",&a,&b);
			addedge(a,b);
		}
		for(int i=1;i<=n;i++)
		if(!dfn[i]) tarjan(i);
		if(num==1)
		{
			printf("-1\n");
			continue;
		}
		for(int i=1;i<=n;i++)
		{
			for(int j=head[i];j!=-1;j=edge[j].nxt)
			{
				int to=edge[j].to;
				if(fa[to]!=fa[i])
				{
					out[fa[i]]++; in[fa[to]]++;
				}
			}
		}
		int M_num=10000000;
		for(int i=1;i<=num;i++)
		{
			if(in[i]==0||out[i]==0)
			M_num=min(M_num,book[i]);
		}
		ll ans=1ll*n*(n-1)-1ll*M_num*(n-M_num);
		
		printf("%lld\n",ans-m);
	}
	return 0;
}

Caocao’s Bridges(割桥板子)

割桥板子题(就是感觉题意不清晰?)
注意两点就能秒了这道题

1. 图不连通直接输出零
2. 炸桥最少也要一个人吧?

ACcode:

#include 
#include 
#include 
#include  
#define ll long long
#define MAX 1010
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
struct node{
	int to,nxt,v;
}edge[MAX*MAX*2];

int head[MAX];
int cnt;
int n,m;
void addedge(int from,int to,int v)
{
	edge[cnt]={to,head[from],v};
	head[from]=cnt++;
}
int dfn[MAX];
int low[MAX];
int vis[MAX];
int ans=10000000;
int len;

void tarjan(int now,int last)
{
	low[now]=dfn[now]=len++;
	vis[now]=1;
	for(int i=head[now];i!=-1;i=edge[i].nxt)
	{
		int to=edge[i].to;
		if(i==(last^1)) continue;
		if(dfn[to]==0)
		{
			tarjan(to,i);
			low[now]=min(low[now],low[to]);
			if(dfn[now]<low[to])
			ans=min(ans,edge[i].v);
		}
		else if(vis[to])
		{
			low[now]=min(low[now],dfn[to]);
		}
	}
	vis[now]=0;
}

void init()
{
	mem(head,-1);
	mem(dfn,0);
	cnt=0;
	len=1;
	ans=10000000;
}

int main()
{
	int n,m;
	while(scanf("%d%d",&n,&m),n||m)
	{
		init();
		int a,b,c;
		for(int i=0;i<m;i++)
		{
			scanf("%d%d%d",&a,&b,&c);
			addedge(a,b,c);
			addedge(b,a,c);
		}
		tarjan(1,-1);
		int f=0;
		for(int i=1;i<=n;i++)
		{
			if(dfn[i]==0)
			{
				f=1;
				break;
			}
		}
		if(f)
		{
			printf("0\n");
			continue;
		}
		printf("%d\n",(ans==10000000? -1:max(1,ans)));
	}
	return 0;
}

P1262 间谍网络

时隔多月,再一次写tarjan简直是有一种怀念 (似曾相识) 的感觉,不过还行,至少敲出来了,题目属于一看就有思路,一写就嫌麻烦的类型,思路很明显,缩点成树,判断根是否能收买,有一个根不能就是"NO",否则就是"YES",总花费就是根的花费的和,NO的就标记所有可以被收买的节点,第一个不能被收买,且没有被标记的节点就是答案(第一发死到粗体字上了…菜!)

二分图匹配

Fire Net HDU - 1045(简单构图+板子)

网格图可以说是有着天然的二部图的影子(行和列分别为二部图的两端,点就是边)

匈牙利板子题,唯一要注意的是建图的时候要把相连的行和列看做一个点.
(话说这题可以暴力来着?)
ACcode:

#include 
#include 
#include 
#define MAX 110
using namespace std;
int n;

char mp[MAX][MAX];
int xid[MAX][MAX];
int yid[MAX][MAX];

struct node{
	int to,nxt;
}edge[MAX*MAX];
int x_max;
int cnt;
int head[MAX];
void addedge(int from,int to)
{
	edge[cnt]={to,head[from]};
	head[from]=cnt++;
}

int vis[MAX];
int match[MAX];

int getit(int now)
{
	for(int i=head[now];i!=-1;i=edge[i].nxt)
	{
		int to=edge[i].to;
		if(vis[to]) continue;
		vis[to]=1;
		if(match[to]==0||getit(match[to]))
		{
			match[to]=now;
			return 1;
		}
	}
	return 0;
}

void getans()
{
	int ans=0;
	for(int i=1;i<=x_max;i++)
	{
		memset(vis,0,sizeof(vis));
		if(getit(i))
		ans++;
	}
	printf("%d\n",ans);
}

void init()
{
	memset(xid,0,sizeof(xid));
	memset(yid,0,sizeof(yid));
	memset(head,-1,sizeof(head));
	memset(match,0,sizeof(match));
	cnt=0;
}

int main()
{
	
	while(scanf("%d",&n),n)
	{
		init();
		int id=0;
		for(int i=1;i<=n;i++)
		scanf("%s",mp[i]+1);
		int f=0;
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=n;j++)
			{
				if(mp[i][j]=='X') f=0;
				else
				{
					if(f==0) 
					{
						f=1;
						id++;
					}
					xid[i][j]=id;
				}
			}
			f=0;
		}
		x_max=id;
		f=0;
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=n;j++)
			{
				if(mp[j][i]=='X') f=0;
				else
				{
					if(f==0) 
					{
						f=1;
						id++;
					}
					yid[j][i]=id;
				}
			}
			f=0;
		}
		
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=n;j++)
			{
				if(mp[i][j]=='.')
				addedge(xid[i][j],yid[i][j]);
			}
		}
		
		getans();
		
	}
	
	return 0;
}

The Accomodation of Students HDU 2444(判断+板子)

题意:先判断是不是二部图,不是输出"No",否则输出最大匹配.
跑一个DFS(染色)就能判断是不是二部图了O(n),然后跑个匈牙利就OK了(nlog(n))

ACcode:

#include
#include 
#include 
#include 
#define MAX 220
using namespace std;
int n,m; 
struct node{
	int to,nxt;
}edge[MAX*MAX*2];

int head[MAX];
int len;

void addedge(int from,int to)
{
	edge[len]={to,head[from]};
	head[from]=len++;
}

int flag[MAX];
int mark;
void dfs(int now,int f)
{
	flag[now]=f;
	for(int i=head[now];i!=-1;i=edge[i].nxt)
	{
		int to=edge[i].to;
		if(flag[to]!=-1)
		{
			if(flag[to]==f) mark=0;
			continue;
		}
		dfs(to,1-f);
	}
}

int vis[MAX];
int march[MAX];

int getit(int now)
{
	for(int i=head[now];i!=-1;i=edge[i].nxt)
	{
		int to=edge[i].to;
		if(vis[to]) continue;
		vis[to]=1;
		if(march[to]==0||getit(march[to]))
		{
			march[to]=now;
			return 1;
		}
	}
	return 0;
}

void getans()
{
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		memset(vis,0,sizeof(vis));
		if(flag[i]==1&&getit(i))
		ans++;
	}
	printf("%d\n",ans);
}

void init()
{
	memset(head,-1,sizeof(head));
	memset(flag,-1,sizeof(flag));
	memset(march,0,sizeof(march));
	len=0;
	mark=1;
}

int main()
{
	while(scanf("%d%d",&n,&m)!=EOF)
	{
		init();
		int a,b;
		for(int i=0;i<m;i++)
		{
			scanf("%d%d",&a,&b);
			addedge(a,b);
			addedge(b,a);
		}
		for(int i=1;i<=n;i++)
		{
			if(flag[i]==-1)
			dfs(i,1);
		}
		if(mark==0)
		{
			printf("No\n");
			continue;
		}
		getans();
	}
	return 0;
}

Courses HDU - 1083(板子)

因为实在是太板子了,所以不放代码了…(太水了…)

Swap HDU - 2819(网格图的二分图匹配)

传统的网格图,传统的构图方法,传统的匹配,不传统的输出…

如图所示,你显然不能把所有没有对应上的全输出一遍…(废话)
这里我思路错了,一直再找一个顺序来输出,很麻烦,最后也不知道哪里错了…
其实这里的思路很简单,我这一行应该对应其它列,那好,我就和我应该对应的那一列交换,这次交换的结果一定可以让一个对角线上的0变成1,然后我这一行所对应的列就变成了,和我交换的那行所对应的列,如果没有对应上,就接着交换,直到对应上为之(一定可以找到,因为走下来就会发现其实是一个环)

ACcode:

#include 
#include 
#include 
#include 
#include 
#define MAX 220
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;

int n;

struct node{
	int to,nxt;
}edge[MAX*MAX];

pair<int,int> ans[MAX*MAX];

int head[MAX];
int cnt;

void addedge(int from,int to)
{
	edge[cnt]={to,head[from]};
	head[from]=cnt++;
}
int march[MAX];
int vis[MAX];
int dfs(int now)
{
	for(int i=head[now];i!=-1;i=edge[i].nxt)
	{
		int to=edge[i].to;
		if(vis[to]) continue;
		vis[to]=1;
		if(march[to]==0||dfs(march[to]))
		{
			march[to]=now;
			return 1;
		}
	}
	return 0;
}

void getans()
{
	int len=0;
	for(int i=1;i<=n;i++)
	{
		mem(vis,0);
		if(dfs(i+n))
		len++;
	}
	if(len!=n)
	{
		printf("-1\n");
		return ;
	}
	int k[MAX]={0};
	int m=0;
	for(int i=1;i<=n;i++)
		k[march[i]-n]=i;
	for(int i=1;i<=n;i++)
	{
		while(k[i]!=i)
		{
			ans[++m].first=i;
			ans[m].second=k[i];
			swap(k[k[i]],k[i]);
		}
	}
	printf("%d\n",m); 
	for(int i=1;i<=m;i++)
	printf("R %d %d\n",ans[i].first,ans[i].second);
	
}

void init()
{
	mem(head,-1);
	cnt=0;
	mem(march,0);
}
int main()
{
	while(scanf("%d",&n)!=EOF)
	{
		init();
		for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
		{
			int a;
			scanf("%d",&a);
			if(a)
			addedge(i+n,j);
		}
		getans();
	}
	return 0;
}

Rain on your Parade HDU - 2389(HK)

卡了一上午…只因为一个巨沙雕的错误…佛了
只看题意就是一个巨裸的二分图匹配,但是套匈牙利会愉快的超时…
所以我们要加一个优化,所以就很开心的 (被迫) 学了一个HK算法

其实挺简单的,传统的匈牙利对于下面的图就会显得十分沙雕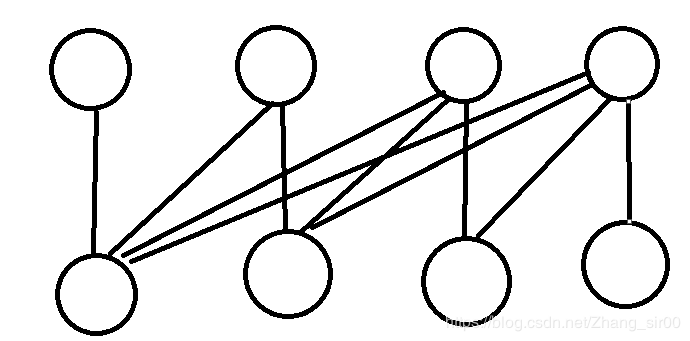
所以我们就先添一个bfs找路,让bfs来指导dfs以至于dfs不会像无头苍蝇乱撞…找路也十分的简单…看一遍bfs应该就理解了,并不难.

ACcode:

#include 
#include 
#include 
#include 
#include 
#include 
#define MAX 3030
#define ll long long
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
int t,n,m;

struct People{
	int x,y,spead;
}p[MAX];

struct node{
	int to,nxt;
}edge[MAX*MAX];

int head[MAX];
int cnt;
int march[MAX+MAX];
int dep[MAX+MAX];

void addedge(int from,int to)
{
	edge[cnt]={to,head[from]};
	head[from]=cnt++;
}

int bfs()
{
	queue<int> que;
	mem(dep,0);
	int flag=0;
	for(int i=1;i<=n;i++)
	{
		if(march[i]==0) que.push(i);
	}
	while(!que.empty())
	{
		int t=que.front();
		que.pop();
		for(int i=head[t];i!=-1;i=edge[i].nxt)
		{
			int to=edge[i].to;
			if(!dep[to])
			{
				dep[to]=dep[t]+1;
				if(march[to]==0) flag=1;
				else
				{
					dep[march[to]]=dep[to]+1;
					que.push(march[to]);
				}
			}
		}
	}
	return flag;
}


int dfs(int now)
{
	for(int i=head[now];i!=-1;i=edge[i].nxt)
	{
		int to=edge[i].to;
		if(dep[to]!=dep[now]+1) continue;
		dep[to]=0;
		if(march[to]==0||dfs(march[to]))
		{
			march[to]=now;
			march[now]=to;
			return 1;
		}
	}
	return 0;
}

void getans()
{
	int ans=0;
	while(bfs())
	{
		for(int i=1;i<=n;i++)
		{
			if(march[i]==0&&dfs(i))
				ans++;
		}
	}
	printf("%d\n\n",ans);
}

bool judge(int x,int y,People a)
{
	ll dis=1ll*(a.x-x)*(a.x-x)+1ll*(a.y-y)*(a.y-y);
	return 1ll*a.spead*t*a.spead*t>=dis;
}

void init()
{
	mem(march,0);
	mem(head,-1);
	cnt=0;
}

int main()
{
	int Q;
	scanf("%d",&Q);
	for(int q=1;q<=Q;q++)
	{
		init();
		printf("Scenario #%d:\n",q);
		scanf("%d",&t);
		scanf("%d",&n);
		for(int i=1;i<=n;i++)
			scanf("%d%d%d",&p[i].x,&p[i].y,&p[i].spead);
		scanf("%d",&m);
		for(int i=1;i<=m;i++)
		{
			int x,y;
			scanf("%d%d",&x,&y);
			for(int j=1;j<=n;j++)
			{
				if(judge(x,y,p[j]))
				{
					addedge(j,i+n);
				}
			}
		}
		getans();
	}
	return 0;
}
/*
1
3
0 0 5
0 0 5
10 0 5
3
-5 0
0 -5
5 0
*/

Oil Skimming HDU - 4185(神奇的建图)

不解释题意了…(懒癌犯了)

这个题看似和二分图匹配没有半毛钱关系(也许只是我太菜了…看不出来)
但是我们把图看成下面这个样子:

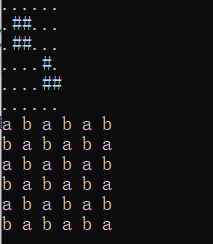
把a所对应的点看成二分图的一半,b对应的点看成二分图的另一半,二分图的每一条边就代表一个可能的匹配,于是这个题就迎刃而解了(神奇的建图思路,要多总结一些)

ACcode:

#include 
#include 
#include 
#define MAX 610
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
struct node{
	int to,nxt;
}edge[MAX*MAX*4];
int head[MAX*MAX];
int cnt;
void addedge(int from,int to)
{
	edge[cnt]={to,head[from]};
	head[from]=cnt++;
}

int fw[4][2]={0,1,0,-1,1,0,-1,0};
int n;

int march[MAX*MAX];
int vis[MAX];
char map[MAX][MAX];

int dfs(int now)
{
	for(int i=head[now];i!=-1;i=edge[i].nxt)
	{
		int to=edge[i].to;
		if(vis[to]) continue;
		vis[to]=1;
		if(march[to]==0||dfs(march[to]))
		{
			march[to]=now;
			return 1;
		}
	}
	return 0;
}


void getans()
{
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		if((i+j)%2==0)
		{
			mem(vis,0);
			if(dfs((i-1)*n+j))
			{
				ans++;
			}
		}
	}
	printf("%d\n",ans);
}



void judge(int x,int y)
{
	for(int i=0;i<4;i++)
	{
		int xx=x+fw[i][0];
		int yy=y+fw[i][1];
		if(xx<1||xx>n||yy<1||yy>n||map[xx][yy]=='.') continue;
		addedge(n*(x-1)+y,n*(xx-1)+yy);
	}
}

void init()
{
	mem(march,0);
	mem(head,-1);
	cnt=0;
}

int main()
{
	int t;
	scanf("%d",&t);
	for(int q=1;q<=t;q++)
	{
		init();
		scanf("%d",&n);
		for(int i=1;i<=n;i++)
		scanf("%s",map[i]+1);
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=n;j++)
			{
				if(map[i][j]=='.'||(i+j)%2==1) continue;
				judge(i,j);
			}
		}
		printf("Case %d: ",q);
		getans();
	}
	return 0;
}

Antenna Placement POJ - 3020(上一道题的练习)

会了上道题,这题就是来送分的…(但还是因为数组开小了这种沙雕错误卡了快一个小时…)
ACcode:

#include 
#include 
#include 
#include 
#define MAX 100
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
int n,m;
int fw[4][2]={0,1,0,-1,1,0,-1,0};
struct node{
	int to,nxt;
}edge[MAX*MAX*4];
int head[MAX*MAX];
int cnt;
char map[MAX][MAX]; 
int sum;//*的总数 
void addedge(int from,int to)
{
	edge[cnt]={to,head[from]};
	head[from]=cnt++;
}

int march[MAX*MAX];
int vis[MAX*MAX];


int dfs(int now)
{
	for(int i=head[now];i!=-1;i=edge[i].nxt)
	{
		int to=edge[i].to;
		if(vis[to]) continue;
		vis[to]=1;
		if(march[to]==0||dfs(march[to]))
		{
			march[to]=now;
			march[now]=to;
			return 1;
		}
	}
	return 0;
}

void getans()
{
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			if(map[i][j]=='*'&&(i+j)%2==0)
			{
				mem(vis,0);
				if(dfs(m*(i-1)+j))
				{
					ans++;
				}
			}
		}
	}
	printf("%d\n",sum-ans);
}


void judge(int x,int y)
{
	for(int i=0;i<4;i++)
	{
		int xx=x+fw[i][0];
		int yy=y+fw[i][1];
		if(xx>n||xx<1||yy>m||yy<1||map[xx][yy]!='*') continue;
		addedge(m*(x-1)+y,m*(xx-1)+yy);
	}
}

void init()
{
	mem(march,0);
	mem(head,-1);
	cnt=0;
	sum=0;
}

int main()
{
	int t;
	scanf("%d",&t);
	while(t--)
	{
		init();
		scanf("%d%d",&n,&m);
		for(int i=1;i<=n;i++)
			scanf("%s",map[i]+1);
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=m;j++)
			{
				if(map[i][j]=='*')
				{
					if((i+j)%2==0)
					judge(i,j);
					sum++;
				}
			}
		}
		getans();
	}
	
	return 0;
}

Strategic Game HDU - 1054(裸的最小点覆盖)

题意:给一棵树,问你最少取几个点,能把所有边全部覆盖完.
前置小知识:

1. 每一棵树都是一个二分图(层数为奇的是二分图的一部分,为偶的是另一部分,二分图的边就是树的边),然后这道题就转化为二分图求最小点覆盖了…
2. 最小点覆盖==最大匹配,证明也挺简单的,当一张二分图达到最大匹配时，左边的点集中未匹配的点肯定不会与右边点集中未匹配的点连接，如果连接，说明含有增广路，可以继续匹配，那么可以得出这么一个结论，达到最大匹配时，左右点集未匹配的点肯定会连接在已匹配的点上(除非你是一个孤立点…).

知道了上边的两点,这个题就可以秒杀了>_ ACcode:

#include 
#include 
#include 
#include 
#include 
#define MAX 1600
#define ll long long
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
int n;
struct node{
	int to,nxt;
}edge[MAX*MAX];
int head[MAX];
int cnt;

void addedge(int from,int to)
{
	edge[cnt]={to,head[from]};
	head[from]=cnt++;
}
int flag[MAX];

void bfs()
{
	queue<int> que;
	flag[0]=0;
	que.push(0);
	while(!que.empty())
	{
		int t=que.front();
		que.pop();
		for(int i=head[t];i!=-1;i=edge[i].nxt)
		{
			int to=edge[i].to;
			if(flag[to]==-1)
			{
				flag[to]=1-flag[t];
				que.push(to);
			}
		}
	}
}
int march[MAX];
int vis[MAX];

int dfs(int now)
{
	for(int i=head[now];i!=-1;i=edge[i].nxt)
	{
		int to=edge[i].to;
		if(vis[to]) continue;
		vis[to]=1;
		if(march[to]==-1||dfs(march[to]))
		{
			march[to]=now;
			return 1;
		}
	}
	
	return 0;
}


void getans()
{
	int ans=0;
	for(int i=0;i<n;i++)
	{
		mem(vis,0);
		if(flag[i]==1&&dfs(i))
		ans++;
	}
	printf("%d\n",ans);
}

void init()
{
	mem(flag,-1);
	mem(head,-1);
	mem(march,-1);
	cnt=0;
}

int main()
{
	while(scanf("%d",&n)!=EOF)
	{
		init();
		for(int i=0;i<n;i++)
		{
			int now,m;
			scanf("%d:(%d)",&now,&m);
			int a;
			for(int j=0;j<m;j++)
			{
				scanf("%d",&a);
				addedge(now,a);
				addedge(a,now);
			}
		}
		bfs();
		getans();
	}
	return 0;
}

Treasure Exploration POJ - 2594(传递闭包+有向图匹配)

做了这么多题了,总是把匈牙利想象在二分图上使用,但这是肤浅的(要尽力的开拓眼界,还要多做题啊,难怪这部分的题比连通图多那么多)

题意很简单:让机器人沿着有向的边走(图无环),问最少用几个机器人(可以在任意一个点开始)能访问到图上所有的点.

图论的问题思路很重要(所有问题思路都很重要吧…),假设没有机器人移动,那么毫无疑问我们要总点数个机器人,然而这些机器人是会动的,每当这个机器人移动到一个以前没有到达过的点,我们所需的总机器人的个数就会减一,
但问题又来了,一个机器人的路径可能会很长,这怎么办呢?如果它走的是A->B->C的路径,他其实等价于A->B和B->C两段路的和所以如果我们硬要把这个图看做二分图的话,其实所有的点都在二分图的一侧,所有的点也都在二分图的另一侧,但我们还不能只考虑相邻的边比如下面这个图:
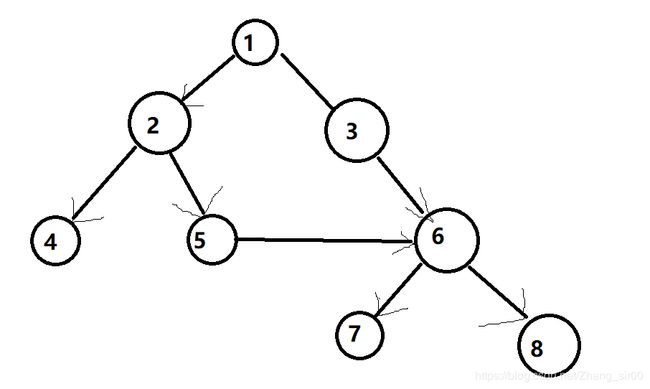(上面的图少了一个1->3的箭头…)

如果只考虑相邻的边,这个图的最大匹配是4,正是因为有一条路跨越了已经匹配过的点,所以被无视掉了,所以我们要利用floyd求一下传递闭包,在传递闭包的图上跑二分图匹配就ok啦>_

ACCode:

#include 
#include 
#include 
#include 
#define mem(a,b) memset(a,b,sizeof(a))
#define MAX 550
using namespace std;
int n,m;
int mp[MAX][MAX];
int march[MAX];
int vis[MAX];

int dfs(int now)
{
	for(int i=1;i<=n;i++)
	{
		if(mp[now][i]==0||vis[i]) continue;
		vis[i]=1;
		if(march[i]==0||dfs(march[i]))
		{
			march[i]=now;
			return 1;
		}
	}
	return 0;
}

void getans()
{
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		mem(vis,0);
		if(dfs(i))
		ans++;
	}
	printf("%d\n",n-ans);
}

void init()
{
	mem(march,0);
	mem(mp,0);
}
int main()
{
	while(scanf("%d%d",&n,&m),n||m)
	{
		init();
		int a,b;
		for(int i=0;i<m;i++)
		{
			scanf("%d%d",&a,&b);
			mp[a][b]=1;
		}
		for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
		for(int k=1;k<=n;k++)
		mp[i][j] |=(mp[i][k]&&mp[k][j]);
		getans();
	}
	return 0;
}
/*
8 8
1 2
1 3
2 4
2 5
5 6
3 6
6 7
6 8
*/

Cat VS Dog HDU - 3829(建图+无向图匹配)

题意:每个孩子都有自己喜欢的动物和讨厌的动物,如果把这个孩子讨厌的动物移走而保留这个孩子喜欢的动物,那么这个孩子就会高兴,现在问最多能使几个孩子高兴.

匈牙利的题写的也挺多的了,但是遇到问题依然没有办法自己独立的解决,总感觉哪里理解的不到位,导致思路一到关键的地方就卡壳,既然如此,那就用最笨的方法,对每一道题,把它与以前做过的题做对比,找到,自己卡壳的关键,这个题导致卡壳的地方有两个,
一个是建图,以前的想法是把动物作为二分图的顶点,这种想法不可取,一是因为有重边,二是因为没有办法锁定那个动物该舍弃.然后想了半天终于想到是不是应该以孩子作为顶点呢?但是很可惜,没有想到如何建边…(建图真的是一门很重要的本领啊)
另一个是对无向图的匹配不熟练,以前的处理总是避免出现无向图,但没想到有这种强制无向图的题…于是被迫的分析了一波无向图的匹配.其实分析以后也挺简单的,就是分析的过程很痛苦…虽说最大匹配就是简单的除了一个2,但是个人觉得还是应该仔细的跑一遍算法,理解的可能会更透彻一点…

言归正传,这道题在搞定了上面两点之后就可以秒杀了(也没剩下什么别的东西了吧…)
首先是建图,这里我们吧孩子当做二分图的节点(左右对称的那种二分图)如果孩子a喜欢的动物与孩子b讨厌的动物相同,那就说明这俩孩子没有办法共同高兴,我们就在他们之间建一条边,最后求出最大匹配的结果就是我们找到的不能共同高兴的孩子的个数,除以二,就是有几对孩子无法共同高兴,总数减掉就ok了.

ACCode:

#include 
#include 
#include 
#define MAX 550
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
int n;
char like[MAX][5];
char dislike[MAX][5];

struct node{
	int to,nxt;
}edge[MAX*MAX];
int head[MAX];
int cnt;

void addedge(int from,int to)
{
	edge[cnt]={to,head[from]};
	head[from]=cnt++;
}
int vis[MAX];
int march[MAX];
int dfs(int now)
{
	for(int i=head[now];i!=-1;i=edge[i].nxt)
	{
		int to=edge[i].to; 
		if(vis[to])	continue;
		vis[to]=1;
		if(march[to]==0||dfs(march[to]))
		{
			march[to]=now;
			return 1;
		}
	}
	return 0;
}

void init()
{
	mem(march,0);
	mem(head,-1);
	cnt=0;
}

int main()
{
	int c,d;
	while(scanf("%d%d%d",&c,&d,&n)!=EOF)
	{
		init();
		for(int i=1;i<=n;i++)
			scanf("%s%s",like[i],dislike[i]);
		for(int i=1;i<=n;i++)
		{
			for(int j=i+1;j<=n;j++)
			{
				if(!strcmp(like[i],dislike[j])||!strcmp(dislike[i],like[j]))
				{
					addedge(i,j);
					addedge(j,i);
				}
			}
		}
		int ans=0;
		for(int i=1;i<=n;i++)
		{
			mem(vis,0);
			if(dfs(i))
			ans++;
		}
		printf("%d\n",n-ans/2);
	}
	return 0;
}

Jamie’s Contact Groups POJ - 2289(二分/贪心+多重匹配)

题意:给出每个人可能的分组,让人数最多的组的人数尽可能的少,输出人数最多的组的人数.

这道题就是考虑一下多重匹配就好,二分和贪心都可以写(似乎没有人用贪心写?明明贪心比二分快啊…),其实多重匹配真的很简单…

二分就不解释了,贪心就是尽量维持人数最多的组的人数最少,如果如论加入哪个组都能使最大的人数不变,那就随便加入一组,然后最大人数自增1.

二分ACCode:

#include 
#include 
#include 
#include 
#define MAX 2020
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
int n,m;
struct node{
	int to,nxt;
}edge[MAX*MAX];
int head[MAX];
int cnt;

void addedge(int from,int to)
{
	edge[cnt]={to,head[from]};
	head[from]=cnt++;
}

vector<int> march[MAX];
int vis[MAX];

int dfs(int now,int k)
{
	for(int i=head[now];i!=-1;i=edge[i].nxt)
	{
		int to=edge[i].to;
		if(vis[to]) continue;
		vis[to]=1;
		if(march[to].size()<k)
		{
			march[to].push_back(now);
			return 1;
		}
		for(int j=0;j<march[to].size();j++)
		{
			if(dfs(march[to][j],k))
			{
				march[to][j]=now;
				return 1;
			}
		}
	}
	return 0;
}

int juage(int k)
{
	for(int i=0;i<MAX;i++)
	march[i].clear();
	for(int i=1;i<=n;i++)
	{
		mem(vis,0);
		if(dfs(i,k)==0)
		{
			return 0;
		}
	}
	return 1;
}

void init()
{
	mem(head,-1);
	cnt=0;
}

int main()
{
	while(scanf("%d%d",&n,&m),n||m)
	{
		init();
		char name[20];
		for(int i=1;i<=n;i++)
		{
			scanf("%s",name);
			char k;
			while(k=getchar(),k!='\n')
			{
				int a;
				scanf("%d",&a);
				addedge(i,a+n+1);
			}
		}
		int l=0;int r=n;
		while(l<r)
		{
			int mid=(l+r)>>1;
			if(juage(mid)) r=mid; 
			else
			l=mid+1;
		}
		printf("%d\n",l);
	}
	return 0;
}

贪心ACCode:

#include 
#include 
#include 
#include 
#define MAX 2020
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
int n,m;
struct node{
	int to,nxt;
}edge[MAX*MAX];
int head[MAX];
int cnt;
void addedge(int from,int to)
{
	edge[cnt]={to,head[from]};
	head[from]=cnt++;
}

vector<int> march[MAX];
int vis[MAX];
int M;
int dfs(int now,int f)
{
	for(int i=head[now];i!=-1;i=edge[i].nxt)
	{
		int to=edge[i].to;
		if(vis[to]) continue;
		vis[to]=1;
		if(march[to].size()<M)
		{
			march[to].push_back(now);
			return 1;
		}
		for(int j=0;j<march[to].size();j++)
		{
			if(dfs(march[to][j],0))
			{
				march[to][j]=now;
				return 1;
			}
		}
	}
	if(f==1)
	{
		int well=edge[head[now]].to;
		march[well].push_back(now);
		M++;
	}
	return 0;
}

void getans()
{
	for(int i=1;i<=n;i++)
	{
		mem(vis,0);
		dfs(i,1);
	}
}

void init()
{
	mem(head,-1);
	cnt=0;
	for(int i=0;i<MAX;i++)
	march[i].clear();
	M=1;
}

int main()
{
	while(scanf("%d%d",&n,&m),n||m)
	{
		init();
		char name[20];
		for(int i=1;i<=n;i++)
		{
			scanf("%s",name);
			char k;
			while(k=getchar(),k!='\n')
			{
				int a;
				scanf("%d",&a);
				addedge(i,a+n+1);
			}
		}
		getans();
		cout<<M<<endl;
	}
	return 0;
}

Optimal Milking POJ - 2112(最短路+二分+多重匹配)

就是比上一道题多了一个Floyd…结果还写错了,wa了半天…(感觉也能用贪心?以后再说吧,累了…)

ACCode:

#include 
#include 
#include 
#include 
#include 
#define inf 100000000
#define MAX 250
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
int n,m,k;
int mp[MAX][MAX];
int vis[MAX];
vector<int> march[MAX];

int dfs(int now,int mid)
{
	for(int i=1;i<=n;i++)
	{
		if(mp[now][i]>mid||vis[i]) continue;
		vis[i]=1;
		if(march[i].size()<k)
		{
			march[i].push_back(now);
			return 1;
		}
		for(int j=0;j<march[i].size();j++)
		{
			if(dfs(march[i][j],mid))
			{
				march[i][j]=now;
				return 1;
			}
		}
	}
	return 0;
}

int judge(int mid)
{
	for(int i=0;i<MAX;i++)
	march[i].clear();
	for(int i=n+1;i<=n+m;i++)
	{
		mem(vis,0);
		if(dfs(i,mid)==0) return 0;
	}
	return 1;
} 

int main()
{
	while(scanf("%d%d%d",&n,&m,&k)!=EOF)
	{
		for(int i=1;i<=(n+m);i++)
		{
			for(int j=1;j<=(n+m);j++)
			{
				scanf("%d",&mp[i][j]);
				if(mp[i][j]==0) mp[i][j]=inf;
			}
		}
		
		for(int k=1;k<=(n+m);k++)
		for(int i=1;i<=(n+m);i++)
		for(int j=1;j<=(n+m);j++)
		mp[i][j]=min(mp[i][j],mp[i][k]+mp[k][j]);
		
		int l=0;int r=inf;
		while(l<r)
		{
			int mid=(l+r)>>1;
			if(judge(mid))
				r=mid;
			else
				l=mid+1;
		}
		printf("%d\n",r);
	}
	return 0;
}

奔小康赚大钱 HDU - 2255(KM板子)

题意:中文题面不解释…
km就是用于处理可以完备匹配的二分图的带权匹配的算法,本质还是匈牙利,只是多了一个贪心(对于每个点优先找边权最大的匹配),为了实现这个操作,我们设置了一堆(两个)数组来实现封路和放路的操作(值得学习).
而新添加的slack数组似乎只是为了优化…而且不是很明白slack[j]-=d这一步的具体作用,然而不加上这句会产生编译错误?(啊,神奇的C语言,永远滴神!)
(update:)
对于上面神奇的编译错误初步估计为发生了微小的溢出导致slack被默认转换为ll,而min没有min(ll,int)的重载,所以报错…我把inf 改为0X1f3f3f3f就没有编译错误的…(啊,神奇的C语言,永远滴神!)而且吧slack[j]-=d去掉依然是可以通过的,不知道是数据水,还是这句话确实不需要…
ACCode:

#include 
#include 
#include 
#define MAX 330
#define mem(a,b) memset(a,b,sizeof(a))
#define inf 0x1f3f3f3f

using namespace std;
int n;
int mp[MAX][MAX];
int march_x[MAX];
int march_y[MAX];
int vis_x[MAX];
int vis_y[MAX];
int slack[MAX];
int ext_x[MAX];
int ext_y[MAX];

int dfs(int now)
{
	vis_x[now]=1;
	for(int i=1;i<=n;i++)
	{
		if(vis_y[i]||mp[now][i]==0) continue;
		int d=ext_x[now]+ext_y[i]-mp[now][i];
		if(d==0)
		{
			vis_y[i]=1;
			if(march_y[i]==0||dfs(march_y[i]))
			{
				march_y[i]=now;
				march_x[now]=i;
				return 1;
			}
		}
		else
		slack[i]=min(d,slack[i]);
	}
	return 0;
}

int km()
{	
	for(int i=1;i<=n;i++)
	for(int j=1;j<=n;j++)
	ext_x[i]=max(ext_x[i],mp[i][j]);
	
	for(int i=1;i<=n;i++)
	{
		mem(slack,inf);
		while(1)
		{
			mem(vis_x,0);
			mem(vis_y,0);
			if(dfs(i)) break;
			int d=inf;
			for(int j=1;j<=n;j++)//拓展新的路径
			if(vis_y[j]==0)
			d=min(slack[j],d);
			
			//保证原有的路径不遭到破坏
			for(int j=1;j<=n;j++)
			if(vis_x[j]) ext_x[j]-=d;
			for(int j=1;j<=n;j++)
			if(vis_y[j]) ext_y[j]+=d;
		}
	}
	int ans=0;
	for(int i=1;i<=n;i++)
		ans+=mp[i][march_x[i]];
	return ans;
}


void init()
{
	mem(mp,0);
	mem(march_x,0);
	mem(march_y,0);
	mem(ext_y,0);
	mem(ext_x,0);}

int main()
{
	while(scanf("%d",&n)!=EOF)
	{
		init();
		for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
		scanf("%d",&mp[i][j]);
		
		printf("%d\n",km());
		
	}
	return 0;
}

Tour HDU - 3488(KM练习)

题意:给定n个点, m条有向边,有一个人可以从随意一个点出发,走一圈,回到这个点,问怎么走既可以遍历所有的点,同时还能使总路程最短,求最短距离(可以走多个圈,除了起始点可以访问两次,其余的点都只能访问一次)

原本能秒杀的,结果被该死的重边卡了1小时佛了(感觉salck[j]-=d确实没用)

求最小值的话把边权取反就好了.别的就没有了

ACCode:

#include 
#include 
#include 
#include 
#include 
#define MAX 220
#define mem(a,b) memset(a,b,sizeof(a))
#define inf 0x1f3f3f3f
using namespace std;
int n,m;
int mp[MAX][MAX];
int vis_x[MAX];
int vis_y[MAX];
int march_x[MAX];
int march_y[MAX];
int ext_x[MAX];
int ext_y[MAX];
int slack[MAX];

int dfs(int now)
{
	vis_x[now]=1;
	for(int i=1;i<=n;i++)
	{
		if(mp[now][i]==-inf||vis_y[i]) continue;
		int d=ext_x[now]+ext_y[i]-mp[now][i];
		if(d==0)
		{
			vis_y[i]=1;
			if(march_y[i]==0||dfs(march_y[i]))
			{
				march_y[i]=now;
				march_x[now]=i;
				return 1;
			}
		}
		else
		slack[i]=min(slack[i],d);
	}
	return 0;
}
int km()
{
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			ext_x[i]=max(mp[i][j],ext_x[i]);
	
	for(int i=1;i<=n;i++)
	{
		mem(slack,inf);
		while(1)
		{
			mem(vis_x,0);
			mem(vis_y,0);
			if(dfs(i)) break;
			
			int d=inf;
			for(int j=1;j<=n;j++)
			if(vis_y[j]==0)
			d=min(slack[j],d);
			
			for(int j=1;j<=n;j++)
				if(vis_x[j]) ext_x[j]-=d;
			for(int j=1;j<=n;j++)	
				if(vis_y[j]) ext_y[j]+=d;
		}
	}
	int ans=0;
	for(int i=1;i<=n;i++)
		ans+=mp[i][march_x[i]];
	return -ans;
}

void init()
{
	mem(mp,-inf);
	mem(ext_x,-inf);
	mem(ext_y,0);
	mem(march_x,0);
	mem(march_y,0);
}

int main()
{
	int t;
	scanf("%d",&t); 
	while(t--)
	{
		init();
		scanf("%d%d",&n,&m);
		for(int i=0;i<m;i++)
		{
			int a,b,v;
			scanf("%d%d%d",&a,&b,&v);
			mp[a][b]=max(mp[a][b],-v);
		}
		printf("%d\n",km());
	}
	return 0;
}

匹配问题总结

做了十几道题了匹配问题就先告一段落吧,什么?你问开花树?,那东西是啥?能吃吗?(那个以后再说吧,先把基础打好…QWQ)

十几道题里发现适合二分图的有

1. 网格图(行和列,或者像HDU - 4612那样把格点错开来建图),
2. 有向图(这个好理解,有向图有入度和出度,把原来有向图中的一个点拆成两个点,一个在A集合存入度,一个在B集合,存出度),
3. 树(奇数层,和偶数层分别为二分图的两个集合)
4. 没有奇环的无向图(和树的性质差不多,只是可能没有那么直观)

其实只要能找到二部图的两部分就好,(两部分之间有边儿各部分里边没有边)

匹配可以解决的问题(只有想不到, 没有做不到)

1. 树/有向图找几条路径可以覆盖全部节点.(别忘了要加上一个传递闭包)
2. 树最少几个节点可以吧所有边覆盖.
3. 最大匹配(字面意思)
4. 分组(使得最大组人数最少)
5. 寻找矛盾的数目(详见 HDU - 3829)等其它一些奇奇怪怪的问题…

然后再来说一下匹配的具体算法(带花树等一切我没有列到的算法不算…太菜了不会…)

1. 匈牙利(最根本的算法,一切我所知道的 匹配算法的来源)(O(VE))
2. HK(匈牙利+bfs找路,对匈牙利在部分特殊情况下有很大的优化)(O(sqrt(V)*E))至于为什么是sqrt(V)?别问,问就是量子力学
3. 多重匹配(没错!它简单的不配拥有姓名).
4. KM(带权值的匹配,相比于匈牙利,多了一个封路操作,算法本质就是一个贪心,话说匈牙利的本质不就是暴力嘛?无误 )

匈牙利的算法因为复杂度的问题,一般就是200个点左右,1000个点就要用HK,再大一点就不用考虑匹配了>_

ok!,下一站,网络流!

网络流

Dining POJ - 3281(简单建图加网络流板子)

kuangbin的第一道网络流题是真的看不懂题…跪了

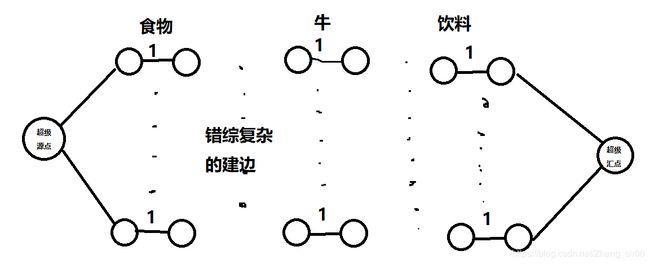
题意很简单,给你n头牛,f个食物,d个饮料,每头牛都只吃他们喜爱的食物和饮料,问你最多能满足几头牛…
如果只有饮料或者只有食物,那就是一个匹配的板子题啊!(所以网络流也可以写匹配题)把图建成下面这样就OK了还是比较水的,这题没用当前弧优化也是可以的…(数据太小)

然后跑板子就OK了

ACCode:

#include 
#include 
#include 
#include 
#include 
#define ll long long
#define mem(a,b) memset(a,b,sizeof(a))
#define MAX 660
#define inf 0x1f3f3f3f
using namespace std;
int n,f,d;
int s,e;
struct node{
	int to,nxt,v;
}edge[MAX<<7];

int head[MAX];
int cnt;

void addedge(int from,int to,int v)
{
	edge[cnt]={to,head[from],v};
	head[from]=cnt++;
}

int vis[MAX];

int bfs()
{
	mem(vis,0);
	queue<int> que;
	vis[s]=1;
	que.push(s);
	while(que.size())
	{
		int u=que.front();
		que.pop();
		for(int i=head[u];i!=-1;i=edge[i].nxt)
		{
			int to=edge[i].to;
			if(edge[i].v==0||vis[to]) continue;
			vis[to]=vis[u]+1;
			que.push(to);
		}
	}
	return vis[e];
}

int dfs(int u,int flow)
{
	if(u==e||flow==0) return flow;
	for(int i=head[u];i!=-1;i=edge[i].nxt)
	{
		int to=edge[i].to;
		int v=edge[i].v;
		if(vis[to]!=vis[u]+1||v==0) continue;
		int k=dfs(to,min(flow,v));
		if(k>0)
		{
			edge[i].v-=k;
			edge[i^1].v+=k;
			return k;
		}
	}
	return 0;
}

void dinic()
{
	int ans=0;
	int k;
	while(bfs())
	{
		while((k=dfs(s,inf))>0) 
		ans+=k;
	}
	printf("%d",ans);
}


void init()
{
	mem(head,-1);
	cnt=0;
	s=0;
}

int main()
{
	init();
	scanf("%d%d%d",&n,&f,&d);
	e=2*(n+f+d)+1;
	for(int i=1;i<=f;i++)
	{
		addedge(s,i,inf);
		addedge(i,s,0);
	}
	for(int i=1;i<=f;i++)
	{
		addedge(i,i+f,1);
		addedge(i+f,i,0);
	}
	for(int i=1;i<=n;i++)
	{
		addedge(2*f+i,2*f+n+i,1);
		addedge(2*f+n+i,2*f+i,0);
	}
	for(int i=1;i<=d;i++)
	{
		addedge(2*f+2*n+i,2*f+2*n+d+i,1);
		addedge(2*f+2*n+d+i,2*f+2*n+i,0);
	}
	for(int i=1;i<=d;i++)
	{
		addedge(2*f+2*n+d+i,e,1);
		addedge(e,2*f+2*n+d+i,0);
	}
	for(int i=1;i<=n;i++)
	{
		int a,b,c;
		scanf("%d%d",&a,&b);
		for(int j=0;j<a;j++)
		{
			scanf("%d",&c);
			addedge(f+c,2*f+i,inf);
			addedge(2*f+i,f+c,0);
		}
		for(int j=0;j<b;j++)
		{
			scanf("%d",&c);
			addedge(2*f+n+i,2*f+2*n+c,inf);
			addedge(2*f+2*n+c,2*f+n+i,0);
		}
	}
	dinic();
	return 0;
}

A Plug for UNIX POJ - 1087(简单构图加网络流板子)

题意:给你几个插座,给你几个要充电的电器,给你几种插座之间转换的适配器,问你最多有几个插座充不上电.板子题++,唯一被坑的一发是B X的意思是X->B而且不提供B->X的功能…

因为板子部分是一样的,这里贴见图的代码了:
part of ACCode:

void build()
{
	e=mp.size()+1; 
	for(int i=1;i<e;i++)
	{
		if(in[i])
		{
			addedge(s,i,in[i]);
		}
		if(out[i])
		addedge(i,e,out[i]);
	}
	for(int i=0;i<n;i++)
	{
//		addedge(p[i].first,p[i].second,inf);  被这句话坑了一发QWQ
		addedge(p[i].second,p[i].first,inf);
	}
}

int main()
{
	init();
	cin>>n;
	string a,b;
	for(int i=0;i<n;i++)
	{
		cin>>a;
		if(mp[a]==0) mp[a]=mp.size();
		in[mp[a]]++;
	}
	scanf("%d",&sum);
	for(int i=0;i<sum;i++)
	{
		cin>>b>>a;
		if(mp[a]==0) mp[a]=mp.size();
		out[mp[a]]++;
	}
	scanf("%d",&n);
	for(int i=0;i<n;i++)
	{
		cin>>a>>b;
		if(mp[a]==0) mp[a]=mp.size();
		if(mp[b]==0) mp[b]=mp.size();
		p[i]=make_pair(mp[a],mp[b]);
	}
	
	build();
	dinic();
	return 0;
}

Going Home POJ - 2195(二分图带权匹配的网络流写法||费用流)

费用流很简单,就是在网络流的基础之上吧单纯的找路改为找最短路就ok了…这个题的数据很小,想怎么写就怎么写(也没有卡spfa)
整个网络流(费用流)算法的核心就是再重复找路删路的过程…
ACCode:

#include 
#include 
#include 
#include 
#include 
#define ll long long
#define mem(a,b) memset(a,b,sizeof(a))
#define MAX 220 
#define inf 0x3f3f3f3f
using namespace std;
int n,m;
int s,e;
char mp[MAX][MAX];
struct node{
	int to,nxt,v,cost;
}edge[MAX<<7];
int head[MAX];
int cnt;

void addedge(int from,int to,int v,int cost)
{
	edge[cnt]={to,head[from],v,cost};
	head[from]=cnt++;
	edge[cnt]={from,head[to],0,-cost};
	head[to]=cnt++;
}


int h[MAX];//·¿×ÓµÄλÖà 
int len,p;//·¿×ÓµÄÊýÄ¿ºÍÈ˵ÄÊýÄ¿ 

int vis[MAX];
int dis[MAX];
int path[MAX];

int spfa()
{
	mem(vis,0);
	mem(dis,inf);
	mem(path,-1);
	queue<int> que;
	que.push(s);
	dis[s]=0;
	vis[s]=1;
	while(que.size())
	{
		int t=que.front();
		que.pop();
		vis[t]=0;
		for(int i=head[t];i!=-1;i=edge[i].nxt)
		{
			int to=edge[i].to;
			int v=edge[i].v;
			int cost=edge[i].cost;
			if((dis[to]<=dis[t]+cost)||v==0) continue;
			dis[to]=dis[t]+cost;
			path[to]=i;
			if(vis[to]==0)
			{
				vis[to]=1;
				que.push(to);
			}
		}
	}
	if(dis[e]==inf) return 0;
	return 1;
}


void getans()
{
	int ans=0;
	while(spfa())
	{
		int flow=inf;
		for(int i=path[e];i!=-1;i=path[edge[i^1].to])
		{
			flow=min(flow,edge[i].v);
//			cout<"<
		}
		for(int i=path[e];i!=-1;i=path[edge[i^1].to])
		{
			edge[i].v-=flow;
			edge[i^1].v+=flow;
			ans+=flow*edge[i].cost;
		}
	}
	printf("%d\n",ans);
}

void init()
{
	mem(head,-1);
	cnt=0;
	len=0;
	p=0;
	s=0;
}

int main()
{
	while(scanf("%d%d",&n,&m),n||m)
	{
		init();
		for(int i=0;i<n;i++)
		scanf("%s",mp[i]);
		for(int i=0;i<n;i++)
		{
			for(int j=0;j<m;j++)
			{
				if(mp[i][j]=='H') h[++len]=i*m+j;
			}
		}
		int num=1;
		for(int i=0;i<n;i++)
		{
			for(int j=0;j<m;j++)
			{
				if(mp[i][j]=='m')
				{
					++p;
					for(int k=1;k<=len;k++)
					{
						int d=abs(h[k]%m-j)+abs(h[k]/m-i);
						addedge(len+p,k,1,d);
					}
				}
			}
		}
		e=len+p+1;
		for(int i=1;i<=p;i++)
			addedge(0,len+i,1,0);
		for(int i=1;i<=len;i++)
			addedge(i,e,1,0);
//		for(int i=0;i<=e;i++)
//		for(int j=head[i];j!=-1;j=edge[j].nxt)
//		cout<"<
		getans();
	}
	return 0;
}

Minimum Cost POJ - 2516(费用流板子)

这该死的多组样例,卡了我一个小时找BUG,结果是数据没读入完就输出-1,导致下一组样例读入出错…

刚开始把所有点都加进去了,结果发现总点数都1000了,还玩毛线…然后全删了,重新又写了一遍,结果一个板子题硬是写了一晌…(太菜了)

ACCode:

#include 
#include 
#include 
#include 
#include 
#include 
#define MAX 110
#define mem(a,b) memset(a,b,sizeof(a))
#define inf 0x3f3f3f3f
using namespace std;
int n,m,k;
int s,e;
int in[MAX/2][MAX/2];
int out[MAX/2][MAX/2];
struct node{
	int to,nxt,v,cost;
}edge[MAX<<7];
int head[MAX];
int cnt;

void addedge(int from,int to,int v,int cost)
{
	edge[cnt]={to,head[from],v,cost};
	head[from]=cnt++;
	edge[cnt]={from,head[to],0,-cost};
	head[to]=cnt++; 
}

int vis[MAX];
int dis[MAX];
int path[MAX];

int spfa()
{
	mem(dis,inf);
	mem(vis,0);
	mem(path,-1);
	queue<int> que;
	que.push(s);
	vis[s]=1;
	dis[s]=0;
	while(que.size())
	{
		int t=que.front();
		que.pop();
		vis[t]=0;
		for(int i=head[t];i!=-1;i=edge[i].nxt)
		{
			int cost=edge[i].cost;
			int to=edge[i].to;
			int v=edge[i].v;
			if(v==0||dis[to]<=dis[t]+cost) continue;
			dis[to]=dis[t]+cost;
			path[to]=i;
			if(vis[to]==0)
			{
				que.push(to);
				vis[to]=1;
			}
		}
	}
	return dis[e]!=inf;
}

int getans(int &ans,int t)
{
	int sum=0;
	for(int i=1;i<=n;i++)
	sum+=out[i][t];
	int num=0;
	ans=0;
	while(spfa())
	{
		int flow=inf;
		for(int i=path[e];i!=-1;i=path[edge[i^1].to])
		{
			flow=min(flow,edge[i].v);
		}
		for(int i=path[e];i!=-1;i=path[edge[i^1].to])
		{
			edge[i].v-=flow;
			edge[i^1].v+=flow;
			ans+=edge[i].cost*flow;
		}
		num+=flow;
	}
	return sum!=num;
}

void init()
{
	mem(head,-1);
	cnt=0;
	s=0;
	e=n+m+1;
}

int main()
{
	while(scanf("%d%d%d",&n,&m,&k),n||m||k)
	{
		int a;
		for(int i=1;i<=n;i++)
		for(int j=1;j<=k;j++)
		scanf("%d",&out[i][j]);
		for(int i=1;i<=m;i++)
		for(int j=1;j<=k;j++)
		scanf("%d",&in[i][j]);
		int ans=0;
		int f=1;
		for(int t=1;t<=k;t++)
		{
			init();
			for(int i=1;i<=n;i++)
			addedge(m+i,e,out[i][t],0);
			for(int i=1;i<=m;i++)
			addedge(s,i,in[i][t],0);
			
			for(int i=1;i<=n;i++)
			{
				for(int j=1;j<=m;j++)
				{
					scanf("%d",&a);
					addedge(j,m+i,inf,a);
				}
			}
			int cost;
			if(getans(cost,t))
			{
				f=0;
			}
			ans+=cost;
		}
		if(f)
		printf("%d\n",ans);
		else
		printf("-1\n");
	}
	return 0;
}

Power Network POJ - 1459(dinic+当前弧优化)

第一个不用当前弧优化可能会T掉的题…
当前弧很简单(就两行)它仅仅会优化下面的这种情况(但优化效果显著)

因为一个dfs只能跑出来一条路,但是一次bfs可能给你找到很多条路,没有当前弧优化的话,就要傻乎乎的又去跑以前跑过的路了,仅此而已…

其次就是这题的读入是真的狗,无限量空格大放送?

上面是不写当前弧的(在超时的边缘疯狂试探)
下面是写了当前弧优化的(妈妈再也不担心我会超时啦! )

ACCode:

#include 
#include 
#include 
#include 
#include 
#include 
#define ll long long
#define MAX 110
#define mem(a,b) memset(a,b,sizeof(a))
#define inf 0x3f3f3f3f
using namespace std;
int n,m,np,nc;
int s,e;
struct node{
	int to,nxt,v;
}edge[MAX*MAX*2];
int head[MAX];
int cur[MAX];
int cnt;

void addedge(int from,int to,int v)
{
	edge[cnt]={to,head[from],v};
	head[from]=cnt++;
	edge[cnt]={from,head[to],0};
	head[to]=cnt++;
}

int vis[MAX];

int bfs()
{
	mem(vis,0);
	queue<int> que;
	que.push(s);
	vis[s]=1;
	while(que.size())
	{
		int t=que.front();
		que.pop();
		for(int i=head[t];i!=-1;i=edge[i].nxt)
		{
			int to=edge[i].to;
			int v=edge[i].v;
			if(v==0||vis[to]) continue;
			vis[to]=vis[t]+1;
			que.push(to);
		}
	}
	return vis[e];
}

int dfs(int now,int m)
{
	if(now==e||m==0) return m;
	for(int &i=cur[now];i!=-1;i=edge[i].nxt)
	{
		int to=edge[i].to;
		int v=edge[i].v;
		if(vis[to]!=vis[now]+1||v==0) continue;
		int d=dfs(to,min(m,v));
		if(d>0)
		{
			edge[i].v-=d;
			edge[i^1].v+=d;
			return d;
		}
	}
	return 0;
	
}

void getans()
{
	int ans=0;
	while(bfs())
	{
		for(int i=0;i<MAX;i++) cur[i]=head[i];
		int d;
		while((d=dfs(s,inf))>0) ans+=d;
	}
	printf("%d\n",ans);
}

void init()
{
	mem(head,-1);
	cnt=0;
	s=n;
	e=n+1;
}

int main()
{
	while(scanf("%d%d%d%d",&n,&np,&nc,&m)!=EOF)
	{
		getchar();
		init();
		int a,b,c;
		for(int i=0;i<m;i++)
		{
			while(getchar()!='(');
            scanf("%d%*c%d%*c%d",&a,&b,&c);
			addedge(a,b,c);
		}
		for(int i=0;i<np;i++)
		{
			while(getchar()!='(');
            scanf("%d%*c%d",&a,&b);
			addedge(s,a,b);	
		}
		for(int i=0;i<nc;i++)
		{
			while(getchar()!='(');
            scanf("%d%*c%d",&a,&b);
			addedge(a,e,b);	
		}
		getans();
	}
	return 0;
}

Island Transport HDU - 4280(ISPA板子)

这个题用dinic会很卡时间,毕竟有1e5个点,但是边也只有1e5算是稀疏图了?
网上好像也有用dinic卡过去的,但是太极限了9000+MS谁顶得住啊,可能评测机抽一下风就挂了?(尤其是对于我这种只会吧常数写的贼大的选手,)…
于是我就去学习了ISPA,也挺好理解的(本来就是dinic的优化嘛),简单的说一下ISPA还有它的两个优化的思路吧,

ISPA发现了dinic的一个缺点,那就是要不停的bfs,但其实,我们找到一条路之后很多节点的层次压根就没有改变,但是我们还是要搜一遍bfs,只是为了改变少数节点的数值,就显得很没有效率,同时我们还发现了,找到一条通路之后,我们肯定要删除这条路上的至少一条边.这样做只会使得下一条通往终点的通路变长.(也就是说节点的层次只会加大),结合这两点我们就有了ISPA的核心思想,通过一次BFS初始化出所有节点的层次,然后按照这个层次来找通往终点的路径,每找到一条通路就对这条路径进行减流(我暂且这样称呼吧),直到这个节点没有找不到通往下一个节点的路径为止,这时,我们就要进行对层次的修改了,因为我们优先查找最短通路,所以,我们要把层次变为它能指向的节点中层次最小的值+1,如果实在没有通路,就设置为比较大的数值就ok了(表示为路断了就行).这就是ISPA的做法,其中他还有两个优化—当前弧和GAP优化
当前弧不解释,(就是为了避免重复跑路…)优化力度有限,
GAP就厉害了,它的思想是判断当前图源点能否到达汇点,实现起来也就是多了一个数组而已,但优化可以达到100倍左右,很强劲.
GAP实现:就是看看层次中有没有断层,开一个num数组用以记录每个层次的节点数量,当节点的层次发生变化时我们同步修改num数组就ok了.如果发现其中有一个层次的节点数目为0,那就说明没有通路了,结束算法就OK了.

ACCode:

#include 
#include 
#include 
#include 
#include 
#define MAX 100100
#define mem(a,b) memset(a,b,sizeof(a))
#define inf 0x3f3f3f3f
#define ll long long
using namespace std;
int n,m;
int s,e;
int X[MAX];
int num[MAX];
struct node{
	int to,nxt,v;
}edge[MAX*2];
int head[MAX];
int cur[MAX];//当前弧 
int cnt;

void addedge(int from,int to,int v)
{
	edge[cnt]={to,head[from],v};
	head[from]=cnt++;
	edge[cnt]={from,head[to],v};
	head[to]=cnt++;
}

int dis[MAX];
int pre[MAX];

void bfs()
{
	mem(dis,inf);
	dis[e]=0;
	queue<int> que;
	que.push(e);
	while(que.size())
	{
		int t=que.front();
		que.pop();
		for(int i=head[t];i!=-1;i=edge[i].nxt)
		{
			node e=edge[i^1];
			int to=edge[i].to;
			if(dis[edge[i].to]!=inf||e.v==0) continue;
			dis[to]=dis[t]+1;
			que.push(to);
		}
	}
}

int update()
{
	int ans=inf;
	int u=e;
	while(u!=s)
	{
		ans=min(ans,edge[pre[u]].v);
		u=edge[pre[u]^1].to;
	}
	u=e;
	while(u!=s)
	{
		edge[pre[u]].v-=ans;
		edge[pre[u]^1].v+=ans;
		u=edge[pre[u]^1].to;
	}
	return ans;
}


void ISPA()
{
	bfs();
	for(int i=0;i<=n+1;i++)
	num[dis[i]]++;
	int u=s;
	for(int i=0;i<MAX;i++)
	cur[i]=head[i];
	ll ans=0;
	while(dis[s]<=n+1)
	{
//		cout<
		if(u==e)
		{
			ans+=update();
			u=s;
		}
		int f=0;
		for(int &i=cur[u];i!=-1;i=edge[i].nxt)
		{
			int to=edge[i].to;
			int v=edge[i].v;
			if(dis[to]+1==dis[u]&&v)
			{
				f=1;
				pre[to]=i;
				u=to;
				break;
			}
		}
		if(f==0)
		{
			int minn=n+2;
			for(int i=head[u];i!=-1;i=edge[i].nxt)
				if(edge[i].v)
					minn=min(minn,dis[edge[i].to]);
			num[dis[u]]--;
			if(num[dis[u]]==0)
			{
				break;
			}
			dis[u]=minn+1;
			num[minn+1]++;
			cur[u]=head[u];
			if(u!=s)
			u=edge[pre[u]^1].to;
		}
	}
	printf("%lld\n",ans);
}


void init()
{
	mem(head,-1);
	mem(num,0);
	cnt=0;
	s=0;
	e=n+1;
}
int main()
{
	int t;
	scanf("%d",&t);
	while(t--)
	{
		scanf("%d%d",&n,&m);
		init();
		int Min=inf,Max=-inf;
		int a,b,c;
		for(int i=1;i<=n;i++)
		{
			scanf("%d%d",&X[i],&b);
			Min=min(Min,X[i]);
			Max=max(Max,X[i]);
		}

		for(int i=1;i<=n;i++)
		{
			if(X[i]==Min)
			addedge(s,i,inf);
			if(X[i]==Max)
			addedge(i,e,inf);
		}
		for(int i=0;i<m;i++)
		{
			scanf("%d%d%d",&a,&b,&c);
			addedge(a,b,c);
		}
		
		ISPA();
		
	}
	return 0;
}

Food HDU - 4292(Dining POJ - 3281 的强化版+ISPA易错点)

一样的建图,近乎一样的题目描述,不一样的方法(dinic被无情的抛弃了)
详细的代码就不放了,Dining POJ - 3281的图套上ISPA就好,
下面放上我写ISPA时容易踩的坑,

1. 初始化层次的时候不要太大,超过总点数就好,不然num数组可能会溢出…,
2. 一定要分清dis和num数组…我写着写着这俩就搞混了…找了半天BUG…

别的就很简单了.

Control HDU - 4289(最小割+简单建图)

挂了一发因为s和e没改过来…(下次还是再写一遍板子吧…)
这个题是12年ICPC网络赛的签到题,理解题意加简单分析后也不是那么难,但愿今年网络赛能签上到吧…

没啥好说的,挂个建图的代码算了
Part ACCode:

int main()
{
	while(scanf("%d%d",&n,&m)!=EOF)
	{
		init();
		scanf("%d%d",&s,&e);
		s=s*2-1;
		e=e*2;
		int a,b;
		for(int i=1;i<=n;i++)
		{
			scanf("%d",&a);
			addedge(i*2-1,i*2,a);
		} 
		for(int i=1;i<=m;i++)
		{
			scanf("%d%d",&a,&b);
			addedge(2*a,2*b-1,inf);
			addedge(2*b,2*a-1,inf);
		}
//		for(int i=1;i<=2*n;i++)
//		for(int j=head[i];j!=-1;j=edge[j].nxt)
//		cout<"<
		ISPA();
	}
	return 0;
}

网络流小结

按理说网络流才写这么多题应该是没有资格小结的,但是实在是被一个题目恶心到了,目前不是很想写网络流了,先小小的总结一下所得吧,留着坑,以后再补…

网络流可以解决匹配问题 (匈牙利没饭吃了) 但是用网络流解决部分匹配问题确实大材小用 (代码量放着呢…) 但是有些问题匹配确实解决不了 (或者说我太菜了,不会写) 网络流的核心就在于看出它是一道网络流的题, 剩下的就是按照理解的题意建图并套板子(至少做了这几道题,觉得网络流的拓展性不强,板子比较僵化)----抄就完了!

下面是建图的一些心得:

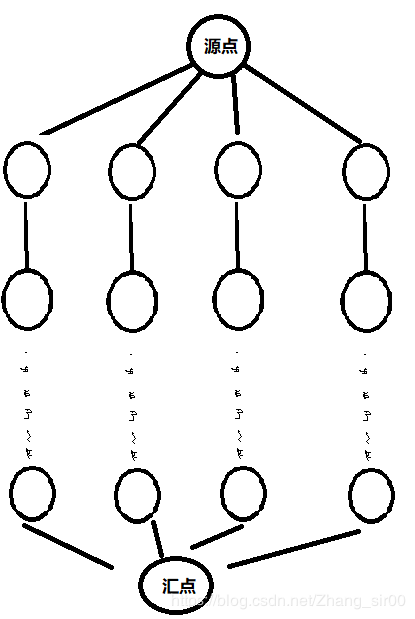
1. 超级源点,超级汇点,没什么好说的,只是为了把多源多汇问题变成网络流可以解决的单源单汇问题而已
2. 拆点,也没什么好说的,就是把对点的限制以边的方式体现出来,还有就是区别处理出度和入度.

似乎没有别的建图技巧了吧?(想到再说)

2-SAT

随便点了一个图论题结果就发现是我不会的品种…那能咋办啊…学呗?
于是在洛谷上找了个板子,看了一堆博客,现在对2-SAT还有三点不理解,以后想到为什么了再来更新,下面把问题列出来:

1. 为什么建立的是有向边,改为无向边会WA.
2. 为什么要找逆拓扑序.
3. tarjan为什么可以求出逆拓扑序.

感觉这三点理解了,2-SAT就很简单了

update:
对第一点的理解: 谁说人家没有反向边啦?只不过人家的反向边是逻辑上的反向…,而按照图论的反向边来看的话,两条边就不是一个意思,瞎搞当然会WA…这种边是看逻辑的…(所以我们要学好离散数学!)

对第二点的理解:这其实是一个贪心策略…因为一旦判断出没有矛盾,那就一定有解(别问什么,量子力学),然后就是找到这个解的问题了
上个图方便理解一下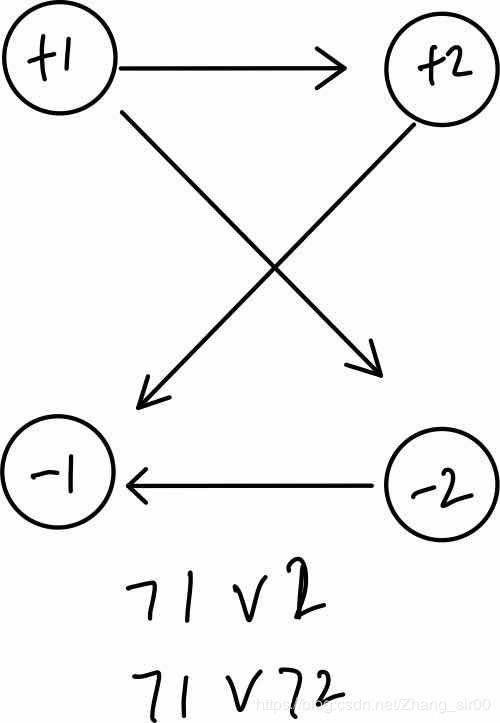

因为我们a->b的意思为如果选择a就一定要选择b,但是选择b不一定一定要选择a,所以为了避免冲突,我们优先选择拓扑序比较大的…(仅此而已)

对于第三点的理解:还没有理解…(先记着吧)

点击这里看板子题
板子:

#include 
#include 
#include 
#include 
#include 
#define MAX 1000010
using namespace std;
int n,m;
struct node{
	int to,nxt;
}edge[MAX*2];
int head[MAX*2];
int cnt;

void addedge(int from,int to)
{
	edge[cnt]={to,head[from]};
	head[from]=cnt++; 
}
stack<int> st;
int color[MAX*2];
int dfn[MAX*2];
int low[MAX*2];
int vis[MAX*2];
int len=1;
int num=0;
void tarjan(int now)
{
	low[now]=dfn[now]=len++;
	st.push(now);
	vis[now]=1;
	for(int i=head[now];i!=-1;i=edge[i].nxt)
	{
		int to=edge[i].to;
		if(dfn[to]==0)
		{
			tarjan(to);
			low[now]=min(low[now],low[to]);
		}
		else if(vis[to])
			low[now]=min(low[now],dfn[to]);
	}
	
	if(low[now]==dfn[now])
	{
		num++;
		while(1)
		{
			int t=st.top();
			st.pop();
			vis[t]=0;
			color[t]=num;
			if(t==now) break;
		}
	}
}


void getans()
{
	for(int i=1;i<=2*n;i++)
	{
		if(dfn[i]==0)
		tarjan(i);
	}
	int f=1;
	for(int i=1;i<=n;i++)
	{
		if(color[i]==color[i+n])
		{
			f=0;
			break;
		}
	}
	if(f)
	{
		printf("POSSIBLE\n");
		for(int i=1;i<=n;i++)
		printf("%d ",color[i]<color[i+n]);
	}
	else
	printf("IMPOSSIBLE\n");
}

void init()
{
	memset(head,-1,sizeof(head));
	cnt=0;
}

int main()
{
	init();
	scanf("%d%d",&n,&m);
	int a,b,c,d;
	for(int i=0;i<m;i++)
	{
		scanf("%d%d%d%d",&a,&b,&c,&d);
		if(b&&d) 
		{
			addedge(a+n,c);
			addedge(c+n,a);
		}
		else if(!b&&d)
		{
			addedge(a,c);
			addedge(c+n,a+n);
		}
		else if(b&&!d)
		{
			addedge(c,a);
			addedge(a+n,c+n);
		}
		else
		{
			addedge(a,c+n);
			addedge(c,a+n);
		} 
	}
//	for(int i=1;i<=2*n;i++)
//	{
//		for(int j=head[i];j!=-1;j=edge[j].nxt)
//		{
//			if(i>n) cout<<"-"<";
//			else cout<";
//			int to=edge[j].to;
//			if(to>n) cout<<"-"<
//			else cout<
//			cout<
//		}
//	}
	getans();
	return 0;
}

练习题

Forming the Council LightOJ - 1251(vjudge上的样例排版有问题,按照样例的格式手动输入就行)

占坑

随时更新…