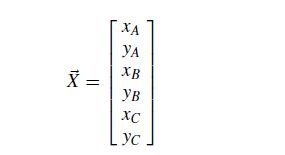A Tutorial on Principal Component Analysis主成分分析教程

主成分分析（PCA）是现代数据分析的中流砥柱 - 黑箱被广泛使用，但（有时）知之甚少。 本文的目标是消除这个黑匣子背后的魔力。 这份手稿的重点在于为主成分分析的工作方式和原因建立坚实的直觉。 本手稿通过从简单的直觉，PCA背后的数学中得出这些知识。 本教程不会回避非正式的解释，也不会回避数学。 希望通过处理这两个方面，各级读者将能够更好地理解PCA

以及何时，如何以及为何应用此技术。

引言

主成分分析（PCA）是现代数据分析中的一种标准工具 - 从神经科学到计算机图形学在不同领域，因为它是从混淆数据集中提取相关信息的简单非参数方法。只需很少的努力PCA提供了路线图 如何将复杂的数据集缩减到较低的维度，以揭示经常出现在其后面的隐藏的，简化的结构。

本教程的目标是为PCA提供直观的感受，并对此主题进行彻底讨论。 我们将从一个简单的例子开始，为PCA的目标提供直观的解释。 我们将继续添加数学严谨性，将其置于线性代数框架内以提供明确的解决方案。 我们将看到PCA与数学技术密切相关的方式和原因

奇异值分解（SVD）。 这种理解将导致我们为如何在现实世界中应用PCA以及对潜在假设的欣赏开辟一条处方。 我希望对PCA有一个透彻的理解，为接近机器学习和尺寸缩减领域提供基础。

本文的讨论和解释是非正式的，本着教程的精神。 本文的目标是教育。偶尔，严格的数学证明是必要的，虽然归入附录。 虽然没有那么重要
教程，这些证明是为希望更全面地理解数学的喜欢冒险的读者提供的。 我唯一的假设是读者对线性代数有一定的了解。 我的目标是提供一个彻底的讨论

通过大量构建线性代数的思想，避免统计和优化理论中的挑战性主题（但请参见讨论）。 请随时与我联系，提供任何建议，更正或评论。

动机：一个玩具的例子

以下是观点：我们是一名实验者。 我们在尝试着通过测量各种数量来了解某些现象（如光谱，电压，速度等）。不幸的是，我们无法弄清楚发生了什么，因为数据显得阴云密布，不清楚，甚至是多余的。这不是一个微不足道的问题，而是一个基本的障碍

在经验科学中。 来自复杂系统的例子很多如神经科学，网络索引，气象学和计算机科学海洋学 - 要测量的变量的数量可以是笨重和有时甚至是欺骗性的，因为潜在的关系往往很简单。

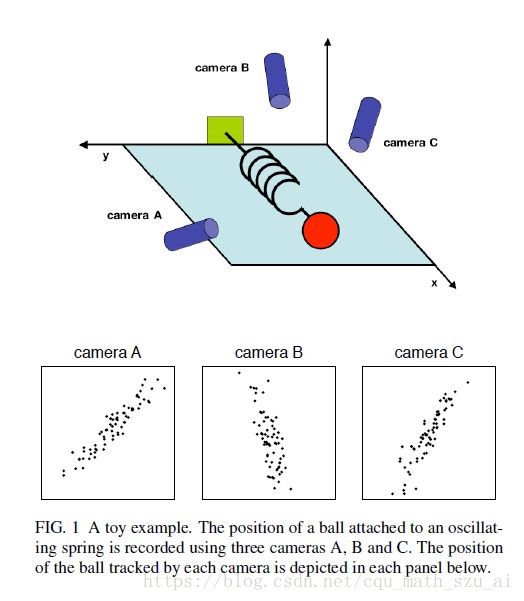
以图1所示的物理学为例，可以举一个简单的玩具问题。假设我们正在研究物理学家的理想弹簧的运动。 这个系统由一个质量球连接到无质量，无摩擦的弹簧组成。 球释放离平衡很小的距离（即弹簧被拉伸）。 因为弹簧是理想的，所以它在设定的频率下围绕x轴平衡无限期地摆动。

这是物理学中的标准问题，其中沿x方向的运动由时间的显式函数来解决。换句话说，基础动力学可以表示为单个变量x的函数。

然而，作为无知的实验者，我们并不知道这个的。 我们不知道哪一个，更不用说有多少个轴和维度是重要的衡量。 因此，我们决定在三维空间测量球的位置（因为我们生活在一个三维世界）。 具体来说，我们放置围绕我们感兴趣的系统的三部电影摄影机 在120赫兹每个电影摄像机记录指示二维的图像球的位置（投影）。 不幸的是，因为我们的无知，我们甚至不知道什么是真实的

x，y和z轴，所以我们选择三个相机位置〜a;〜b和〜c在某些与系统有关的任意角度。 角度在我们的测量之间可能不会是90o！ 现在我们用相机记录几分钟。......最大的问题仍然是：我们如何从这个数据集得到一个简单的x方程？

我们知道，如果我们是聪明的实验者，我们可以用一台相机测量沿x轴的位置。 但这不是现实世界中发生的事情。 我们通常不知道哪些测量结果最能反映我们所讨论系统的动态。 而且，我们有时会记录比实际需要更多的维度。

另外，我们必须处理那个讨厌的，现实世界的噪音问题。 在玩具的例子中，这意味着我们需要处理空气，不完美的相机，甚至是在一个不太理想的弹簧中进行摩擦。 噪音污染了我们的数据集，只会进一步混淆动态。 这个玩具的例子是实验者每天面临的挑战。 在我们深入研究抽象概念时，记住这个例子。 希望在本文的最后，我们将会很好地理解如何使用主成分分析来系统地提取x。

III。 框架：基础的变化

主成分分析的目标是确定重新表达数据集的最有意义的基础。 希望这个新的基础将会滤除噪音并揭示隐藏的结构。 在春季的例子中，PCA的明确目标是确定：“动力学是沿x轴的。”换句话说，PCA的目标是确定x，即沿着x轴的单位基矢量， 轴，是重要的维度。 确定这个事实允许实验者辨别哪些动态是重要的，多余的或噪音。

A. A Naive Basis

通过对我们目标的更精确定义，我们也需要更精确的数据定义。 我们将每次样本（或实验性试验）作为我们数据集中的单个样本进行处理。 在每次采样时，我们记录一组由多次测量组成的数据（例如电压，位置等）。 在我们的数据集中，在某个时间点，摄像机A记录相应的球位置（xA; yA）。 然后可以将一个样本或试验表示为6维列向量

其中每个摄像机将球的位置投影到整个矢量X上。 如果我们以120Hz记录球的位置10分钟，那么我们记录了10？ 60？120 = 72000这些载体。

用这个具体的例子，让我们以抽象的方式重新概括这个问题。 每个样本〜X是一个m维矢量，其中m是测量类型的数量。 等价地，每个样本都是一个位于由一些正交基础所跨越的m维向量空间中的向量。 根据线性代数，我们知道所有测量向量形成这组单位长度基向量的线性组合。 这个正交基础是什么？