李宏毅 机器学习 作业 2 Hungyi.Li Machine Learning HW2 逻辑回归法实现以及优化

关于“一个属性有几个固定选项，怎么表达”的问题，数据采用one-hot，每个选项独立成一个属性，loss用交叉熵计算，这样更科学。这里不用过多操心，数据给出已经处理好了。

 

有一段可能是助教给的参考代码，不过参考代码有些漏洞（在代码下方贴出），需要修改下，然后还有一定的调参提升空间。

 

参考代码如下：

 

import os, sys
import numpy as np
from random import shuffle
import argparse
from math import log, floor
import pandas as pd

# If you wish to get the same shuffle result
# np.random.seed(2401)

def load_data(train_data_path, train_label_path, test_data_path):
    X_train = pd.read_csv(train_data_path, sep=',', header=0)
    X_train = np.array(X_train.values)
    Y_train = pd.read_csv(train_label_path, sep=',', header=0)
    Y_train = np.array(Y_train.values)
    X_test = pd.read_csv(test_data_path, sep=',', header=0)
    X_test = np.array(X_test.values)

    return (X_train, Y_train, X_test)

def _shuffle(X, Y):
    randomize = np.arange(len(X))
    np.random.shuffle(randomize)
    return (X[randomize], Y[randomize])

def normalize(X_all, X_test):
    # Feature normalization with train and test X
    X_train_test = np.concatenate((X_all, X_test))
    mu = (sum(X_train_test) / X_train_test.shape[0])
    sigma = np.std(X_train_test, axis=0)
    mu = np.tile(mu, (X_train_test.shape[0], 1))
    sigma = np.tile(sigma, (X_train_test.shape[0], 1))
    X_train_test_normed = (X_train_test - mu) / sigma

    # Split to train, test again
    X_all = X_train_test_normed[0:X_all.shape[0]]
    X_test = X_train_test_normed[X_all.shape[0]:]
    return X_all, X_test

def split_valid_set(X_all, Y_all, percentage):
    all_data_size = len(X_all)
    valid_data_size = int(floor(all_data_size * percentage))#这个比例反了。

    X_all, Y_all = _shuffle(X_all, Y_all)

    X_train, Y_train = X_all[0:valid_data_size], Y_all[0:valid_data_size]
    X_valid, Y_valid = X_all[valid_data_size:], Y_all[valid_data_size:]

    return X_train, Y_train, X_valid, Y_valid

def sigmoid(z):
    res = 1 / (1.0 + np.exp(-z))
    return np.clip(res, 1e-8, 1-(1e-8))

def valid(w, b, X_valid, Y_valid):
    valid_data_size = len(X_valid)

    z = (np.dot(X_valid, np.transpose(w)) + b)
    y = sigmoid(z)
    y_ = np.around(y)
    result = (np.squeeze(Y_valid) == y_)
    print('Validation acc = %f' % (float(result.sum()) / valid_data_size))
    return

def train(X_all, Y_all, save_dir):

    # Split a 10%-validation set from the training set
    valid_set_percentage = 0.1
    X_train, Y_train, X_valid, Y_valid = split_valid_set(X_all, Y_all, valid_set_percentage)

    # Initiallize parameter, hyperparameter
    w = np.zeros((106,))
    b = np.zeros((1,))
    l_rate = 0.1
    batch_size = 32
    train_data_size = len(X_train)
    step_num = int(floor(train_data_size / batch_size))
    epoch_num = 1000
    save_param_iter = 50

    # Start training
    total_loss = 0.0
    for epoch in range(1, epoch_num):
        # Do validation and parameter saving
        if (epoch) % save_param_iter == 0:
            print('=====Saving Param at epoch %d=====' % epoch)
            if not os.path.exists(save_dir):
                os.mkdir(save_dir)
            np.savetxt(os.path.join(save_dir, 'w'), w)
            np.savetxt(os.path.join(save_dir, 'b'), [b,])
            print('epoch avg loss = %f' % (total_loss / (float(save_param_iter) * train_data_size)))
            total_loss = 0.0
            valid(w, b, X_valid, Y_valid)

        # Random shuffle
        X_train, Y_train = _shuffle(X_train, Y_train)

        # Train with batch
        for idx in range(step_num):
            X = X_train[idx*batch_size:(idx+1)*batch_size]
            Y = Y_train[idx*batch_size:(idx+1)*batch_size]

            z = np.dot(X, np.transpose(w)) + b
            y = sigmoid(z)

            cross_entropy = -1 * (np.dot(np.squeeze(Y), np.log(y)) + np.dot((1 - np.squeeze(Y)), np.log(1 - y)))
            total_loss += cross_entropy

            w_grad = np.sum(-1 * X * (np.squeeze(Y) - y).reshape((batch_size,1)), axis=0)
            b_grad = np.sum(-1 * (np.squeeze(Y) - y))

            # SGD updating parameters
            w = w - l_rate * w_grad
            b = b - l_rate * b_grad

    return

def infer(X_test, save_dir, output_dir):
    test_data_size = len(X_test)

    # Load parameters
    print('=====Loading Param from %s=====' % save_dir)
    w = np.loadtxt(os.path.join(save_dir, 'w'))
    b = np.loadtxt(os.path.join(save_dir, 'b'))

    # predict
    z = (np.dot(X_test, np.transpose(w)) + b)
    y = sigmoid(z)
    y_ = np.around(y)

    print('=====Write output to %s =====' % output_dir)
    if not os.path.exists(output_dir):
        os.mkdir(output_dir)
    output_path = os.path.join(output_dir, 'log_prediction.csv')
    with open(output_path, 'w') as f:
        f.write('id,label\n')
        for i, v in  enumerate(y_):
            f.write('%d,%d\n' %(i+1, v))

    return

def main(opts):
    # Load feature and label
    X_all, Y_all, X_test = load_data(opts.train_data_path, opts.train_label_path, opts.test_data_path)
    # Normalization
    X_all, X_test = normalize(X_all, X_test)

    # To train or to infer
    if opts.train:
        train(X_all, Y_all, opts.save_dir)
    elif opts.infer:
        infer(X_test, opts.save_dir, opts.output_dir)
    else:
        print("Error: Argument --train or --infer not found")
    return

if __name__ == '__main__':
    parser = argparse.ArgumentParser(description='Logistic Regression with Gradient Descent Method')
    group = parser.add_mutually_exclusive_group()
    group.add_argument('--train', action='store_true', default=False,
                        dest='train', help='Input --train to Train')
    group.add_argument('--infer', action='store_true',default=False,
                        dest='infer', help='Input --infer to Infer')
    parser.add_argument('--train_data_path', type=str,
                        default='feature/X_train', dest='train_data_path',
                        help='Path to training data')
    parser.add_argument('--train_label_path', type=str,
                        default='feature/Y_train', dest='train_label_path',
                        help='Path to training data\'s label')
    parser.add_argument('--test_data_path', type=str,
                        default='feature/X_test', dest='test_data_path',
                        help='Path to testing data')
    parser.add_argument('--save_dir', type=str,
                        default='logistic_params/', dest='save_dir',
                        help='Path to save the model parameters')
    parser.add_argument('--output_dir', type=str,
                        default='logistic_output/', dest='output_dir',
                        help='Path to save the model parameters')
    opts = parser.parse_args()
    main(opts)

代码错误有几点：

1.每一个epoch中，用于计算cross_entropy从而统计进total_loss的数据量，是step_num*batch_size，小于train_data_size。而ta

它用的是train_data_size。

这两个数据对比：结果证实，确实有点偏差，不过因为他只是打印，不是训练过程，所以看起来也没影响结果。

2.split_valid_set中，训练集和验证集划分错了，用验证集的比例，提取了训练集。

这个也很明显，会对结果产生显著影响

3.感谢网友weixin_42183288提醒，不过此处确实没错：交叉熵隐含了sum操作！

因为np.dot是点积，点积已经等于sum了，batch_size个样本，最终只输出一维结果，对于batch_size个样本，loss既然是求和，grad也应该是求和，grad要和loss保持同步，所以grad就是sum。

print('epoch avg loss = %f' % (total_loss / (float(save_param_iter) * train_data_size)))

从这句打印也看得出，loss确实是所有样本的和，然后才除以迭代epoch次数和data_size，平均到每个样本。

但是打印归打印，这句不是也说了是avg loss嘛！实际的total loss，还是针对batch的sum。

 

其实这根本不是应该纠结的点！！！这可能是接触代码不多的新手都会碰到的疑惑：

“课程中是除以m，也就是mean”

“loss要用sum还是mean？”

“grad要用sum还是mean？”

“为什么我用mean比用sum感觉要更准一点？”

本质上，这是没区别的，梯度下降，下降的是什么？loss的值！具体loss或者w的大小，只与计算机对小数的表达能力有关（这个角度看，mean反而不如sum准），而不太可能上升到模型准确度差异的高度！教科书是为了示意，如果他想精准地表达梯度，当然要除以m，可是实际计算当中，区别不大。

无论你的grad是用了sum还是mean，最终都是一个数值（乘以参数数量），是数值，在梯度下降时就逃不过乘以l_rate这一环，如果你觉得你用了mean比sum训练结果更准，可以把sum版本对应的l_rate调小一点（实际训练中往往是变动的学习率，越到后期越小）

            w_grad = np.mean(-1 * X * (np.squeeze(Y) - y).reshape((batch_size,1)), axis=0)
            b_grad = np.mean(-1 * (np.squeeze(Y) - y))

            # SGD updating parameters
            w = w - l_rate * w_grad
            b = b - l_rate * b_grad

 

 

 

4.还有个什么错误我忘了。。。。

 

 

上传kaggle，这是两条分数分段线：

0.84952高分

0.84215及格

 

验证集分配错误的，也够及格

0.84803

 

优化的分配比例的：

        X_valid,Y_valid = X_all[0:valid_data_size],Y_all[0:valid_data_size]
        X_train,Y_train = X_all[valid_data_size:],Y_all[valid_data_size:]

0.85159

下边是调整其他参数，batch_size和epoch等：

batch_size提升到64，epoch到5000

0.85356

batch_size提升到64，epoch到5000，l_rate到0.5

0.84201

会下降，猜测可能是没用adagrad，这里不收敛了。

batch_size提升到64，epoch到5000，l_rate改到0.2，

0.85036

比0.5要强，不过还是比0.1差些，也许有运气成分，每次训练也不一样。

batch_size提升到64，epoch到5000，l_rate改到0.05，

 

0.85380目前最优，可能是epoch数量比较大，抵消了learning rate的降低效应。可以明显看到，learning调大明显有收敛问题，所以adagrad可能效果更好。

 

还有训练，集和验证集的比例可以调：

batch_size提升到64，epoch到5000，l_rate改到0.05，验证集改到0.3（默认0.1）

validation acc = 0.851761

实际分数0.85417目前最优，可能说明之前的有过拟合现象。

其他不动，验证集比例改回0.1重新测

validation acc = 0.860258
分数：0.85417，居然一样

本地validation  acc更高一些，实际分数还一样，是有一点过拟合吧？？！！

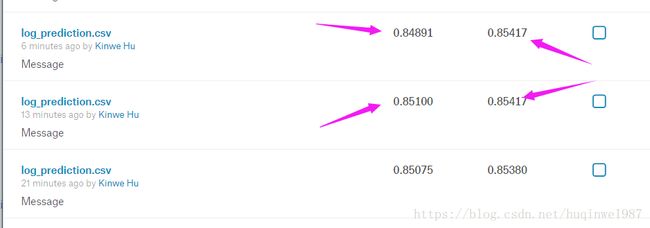
调了一下记录，可以看到倒数第二次，虽然公开的也是0.85417，和最后一次一样，但是最后一次在private衰减到了0.84891，证明最后一次确实比倒数第二次过拟合。

但是过拟合和过拟合也不一样，有两种过拟合，这里说明最后一次是针对线上公开成绩的过拟合，private set发生衰减。

前边说的是针对验证集的过拟合，线上答案发生衰减。

 

紫色字体不算绝对严谨，因为需要更细致的测试对比，每次训练本来就有微小的差距。这里主要讨论可能存在的问题和优化思路，因为时间关系和运算量的关系，就不在这纠结了，先结了。

 

实际跑了一下adagrad，效果飘忽，调起来比较麻烦，时间问题，略过

                w_s_gra = np.zeros(106)
                b_s_gra = np.zeros(1)

                for idx in range(step_num):
                        X = X_train[idx*batch_size:(idx+1)*batch_size]
                        Y = Y_train[idx*batch_size:(idx+1)*batch_size]

                        z = np.dot(X,np.transpose(w))+b

                        y = sigmoid(z)

                        cross_entropy = -1*(np.dot(np.squeeze(Y),np.log(y))+np.dot(1-np.squeeze(Y),np.log(1-y)))
                        total_loss += cross_entropy
                        w_grad = np.mean(-1*X*(np.squeeze(Y)-y).reshape((batch_size,1)),axis=0)
                        b_grad = np.mean(-1*(np.squeeze(Y)-y))



                        w_s_gra += w_grad**2
                        b_s_gra += b_grad**2
                        w_ada = np.sqrt(w_s_gra)
                        b_ada = np.sqrt(b_s_gra)


                        w = w - l_rate * w_grad/w_ada
                        b = b - l_rate * b_grad/b_ada

 

 

可能有编辑错的地方，凑合看吧，实在懒得多写了，这个csdn现在真难用，拼音打一半就自动换行了。