C程序-回溯法（递归形式）解决01背包和n后问题

1. 0-1背包问题

 n=3的0/1背包问题，设物品质量w={18,14,16}; 物品价值v={48,30,30}; 背包容量c=30. 程序如下所示：

#include

using namespace std;

int bestx[3];
int w[3] = { 18, 14, 16 };
int v[4] = { 48, 30, 30 };
int maxValue=0;
//回溯法解决01背包问题
void backTrack(int i, int n, int cw, int cv, int a[], int c);
int main()
{
	//初始条件
	int c = 30;
	int a[3];
	int cw=0, cv=0;
	backTrack(0,3,cw,cv,a,c);
	printf("最大价值：%d",maxValue);
	printf("\n");
	printf("选中情况：");
	for (int i = 0; i < 3;i++)
	{
		printf("%d ",bestx[i]);
	}
	printf("\n");
	return 0;
}

//回溯法解决01背包问题
/*
i：递归深度，遍历树的深度
n：物品个数
cw：当前选中物品总质量
cv：当前选中物品总价值
a：保存可行解的路径
c：背包容量
*/
void backTrack(int i,int n,int cw,int cv,int a[],int c)
{
	//递归的基准情形，当遍历到叶子节点
	if (i >= n)
	{
		if (maxValue

输出结果：

1. n后问题

 等价于在n x n 格的棋盘上放置n个皇后，任何2个皇后不放在同一行或同一列或同一斜线上. 程序如下所示：

#include
#include

using namespace std;
//统计可行解个数
int num = 0;
//回溯法解决n后问题
void QueueTrack(int i, int n, int a[]);
//判断当前皇后位置是否可行
int place(int i, int a[]);

int main()
{
	int a[5] = {0};
	printf("n后问题的可行解如下所示：");
	printf("\n");
	QueueTrack(0, 5, a);
	printf("n后问题可行解个数为：%d",num);
	printf("\n");
	return 0;
}

//回溯法解决n后问题
/*
i：递归深度
n：皇后人数
a：存放可行解
*/
void QueueTrack(int i,int n,int a[])
{
	//递归结束，输出当前可行解
	if (i>=n)
	{
		num++;
		for (int i = 0; i < n;i++)
		{
			printf("%d ", a[i]);
		}
		printf("\n");
	}
	else
	{
		//每个皇后都有n个位置可遍历
		for (int j = 0; j < n;j++)
		{
			a[i] = j;
			//当前位置可行，继续向下递归
			if (place(i,a))
			{
				QueueTrack(i+1,n,a);
			}
		}
	}
}

//判断当前皇后位置是否可行
int place(int i,int a[])
{
	for (int k = 0; k < i; k++)
	{
		if ((abs(k - i) == abs(a[k] - a[i])) || a[i] == a[k])
		{
			return 0;
		}
	}

	return 1;
}

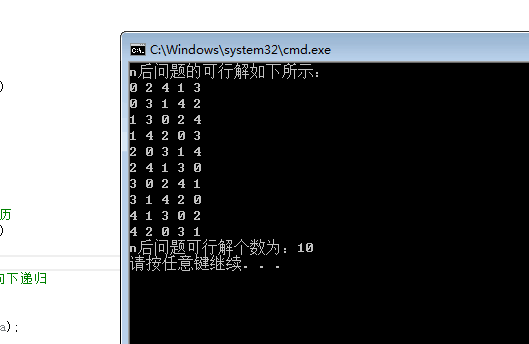
输出结果：