动态规划解决找零钱问题
动态规划算法通常用于求解具有某种最优性质的问题。动态规划算法与分治法类似,其基本思想都是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合于用动态规划求解的问题,经分解得到的子问题往往不是互相独立的。如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。我们可以用一个表(备用表)来记录所有已解的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。这就是动态规划法的基本思路。
下面演示如何通过动态规划算法来解决找零钱问题,以及如何处理该问题的变种情况。
问题描述:
现存在一堆面值为 1,2,5,11,20,50 面值的硬币,问最少需要多少个硬币才能找出总值为 N个单位的零钱
解决这个问题其实也可以考虑使用贪心算法,每次使用面值最大的硬币,不足部分再用小额硬币补充。以兑换63元为例,可选择的硬币和方案为50+11+2。但是,使用贪心算法只能保证每一步取的是局部最优解,并不能保证最终结果是全局最优解。以兑换15元为例,贪心算法给出的组合方案为{11,1,1,1,1},但其实最优方案为{5,5,5}。
使用动态规划算法就能避免该问题。因为动态规划可以保证每次取到的子问题的解是最优解。
动态规划算法思路:
记d{n}={}表示兑换面值为n的最优解组合为{x1,x2,x3...}
从子问题出发,取0元只有一种方法为{0},即d(0)={0},取1元(0+1)元,最优解为1元+0元,即d(0)+1={0,1}={1};
取2元有两种方式,即d(0)+2={2}或d(1)+1={1,1},易知最化解为{2}......
以此累推,兑换面值为n的最优解为d(n)=max{d(n-i)+i},其中(i<=n)
当硬币数量无限时,程序代码如下
import java.util.HashMap;
import java.util.Map;
public class CoinChange {
/**
* @param coins 保存每一种硬币的币值的数组
* @param money 需要找零的面值
*/
public static void changeCoins(int[] coins,int money) {
int[] coinsUsed = new int[money + 1]; // 保存面值为i的纸币找零所需的最小硬币数
int valueKinds = coins.length; //硬币种类数量
coinsUsed[0] = 0; //0元的最优解
Map> coinChangeMap = new HashMap>();
for (int cents = 1; cents <= money; cents++) {
// 当用最小币值的硬币找零时,所需硬币数量最多
int minCoins = cents;
HashMap minCoinMap = new HashMap();//保存各个面值的具体找零方案
minCoinMap.put(1, cents);
coinChangeMap.put(cents, minCoinMap);
// 遍历每一种面值的硬币,看是否可作为找零的其中之一
for (int kind = 0; kind < valueKinds; kind++) {
int coinVal = coins[kind];
int oppCoinVal = cents - coinVal;
if (coins[kind] <= cents) { // 若当前面值的硬币小于当前的cents则分解问题并查表
int tmpCount = coinsUsed[oppCoinVal] + 1;
if (tmpCount <= minCoins) {
HashMap subMap = coinChangeMap.get(oppCoinVal);//子问题的最优解
HashMap tmpMap = new HashMap();
if(subMap != null){//要copy一份数据
tmpMap.putAll(subMap);
}
if(tmpMap.containsKey(coins[kind])){//如果已经包含当前面值,则加一
tmpMap.put(coins[kind], subMap.get(coins[kind])+1);
}else{
tmpMap.put(coins[kind], 1);
}
minCoins = tmpCount;
minCoinMap = tmpMap;
}
}
}
// 保存最小硬币数
coinsUsed[cents] = minCoins;
coinChangeMap.put(cents, minCoinMap);
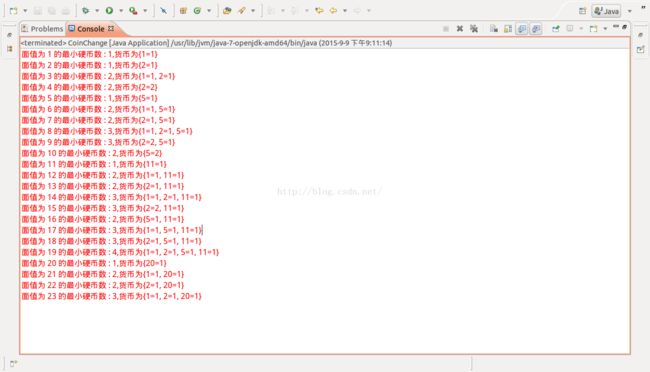
System.err.println("面值为 " + (cents) + " 的最小硬币数 : "
+ coinsUsed[cents]+",货币为"+ coinChangeMap.get(cents));
}
}
public static void main(String[] args) {
// 硬币面值预先已经按降序排列
int[] coinValue = new int[] { 50, 20, 11, 5, 2,1 };
// 需要找零的面值
int money = 23;
// 保存每一个面值找零所需的最小硬币数,0号单元舍弃不用,所以要多加1
changeCoins(coinValue, money);
}
} 
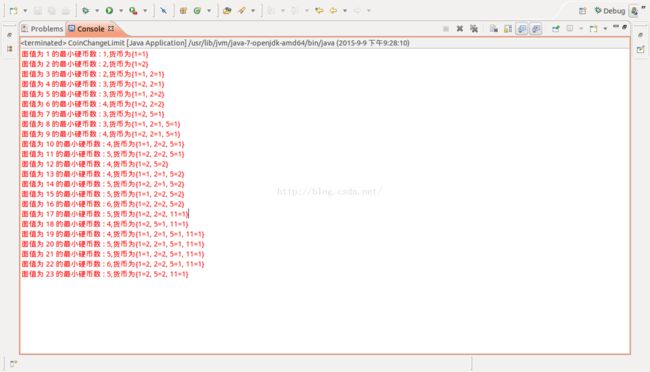
假设硬币的数量是有限的,都为2枚,则每个子问题在得到最优解的时候,应该再判断自己拥有的是否大于需要的,以及当前组合的价值是否刚好等于当前的子问题价值~!
当硬币数量有限时,程序代码如下
import java.util.HashMap;
import java.util.Iterator;
import java.util.Map;
public class CoinChangeLimit {
/**
* @param coins 保存每一种硬币的币值的数组
* @param money 需要找零的面值
*/
public static void changeCoins(int[] coins, int money) {
Map> coinChangeMap = new HashMap>();
Map ownedMap = new HashMap(); //拥有的硬币种类及数量
int valueKinds = coins.length;
for (int kind = 0; kind < valueKinds; kind++) {
ownedMap.put(coins[kind],2);
}
for (int cents = 1; cents <= money; cents++) {
// 当用最小币值的硬币找零时,所需硬币数量最多
int minCoins = cents;
HashMap minCoinMap = new HashMap();
coinChangeMap.put(cents, minCoinMap);
// 遍历每一种面值的硬币,看是否可作为找零的其中之一
for (int kind = 0; kind < valueKinds; kind++) {
// 若当前面值的硬币小于当前的cents则分解问题并查表
int coinVal = coins[kind];
int oppCoinVal = cents - coinVal;
if (coins[kind] <= cents) {
int tmpCount = getCoinCount(coinChangeMap.get(oppCoinVal))+1;
if (tmpCount <= minCoins) { //要用等号
HashMap subMap = coinChangeMap.get(oppCoinVal);//子问题的最优解
HashMap tmpMap = new HashMap();
if(subMap != null){//要copy一份数据
tmpMap.putAll(subMap);
}
if(tmpMap.containsKey(coins[kind])){//如果已经包含当前面值,则加一
tmpMap.put(coins[kind], subMap.get(coins[kind])+1);
}else{
tmpMap.put(coins[kind], 1);
}
//确保拥有的数量大于等于结果数量且价值没有损失
if(isMapCoverSubMap(ownedMap, tmpMap)
&& getCoinsValue(tmpMap) == cents){
minCoinMap = tmpMap;
}
}
}
}
// 保存最小硬币数
coinChangeMap.put(cents, minCoinMap);
System.err.println("面值为 " + (cents) + " 的最小硬币数 : "
+getCoinCount(coinChangeMap.get(cents))+",货币为"+ coinChangeMap.get(cents));
}
}
/**
* 判断mapA是否完全覆盖mapB
* 如a为1=3,2=4 b为1=0,2=1,a完全覆盖b
* 如a为1=3,2=4 b为2=1,3=4,a没有覆盖b
*/
public static boolean isMapCoverSubMap(Map A,Map B){
if(A == null) return false;
if(B == null || B.size() <= 0) return true;
Map.Entry aEntry = null;
Iterator> iter = B.entrySet().iterator();
while(iter.hasNext()){
aEntry = iter.next();
int keyB = aEntry.getKey();
if(!A.containsKey(keyB)) return false;
if(A.get(keyB) < aEntry.getValue()) return false;
}
return true;
}
/**
* 返回当前硬币组合的总价值
*/
public static int getCoinsValue(Map coinMap){
if(coinMap == null ) return 0;
int sum = 0;
Map.Entry aEntry = null;
Iterator> iter = coinMap.entrySet().iterator();
while(iter.hasNext()){
aEntry = iter.next();
sum += aEntry.getKey() * aEntry.getValue();
}
return sum;
}
/**
* 返回当前硬币组合的硬币总数量
*/
public static int getCoinCount(Map B){
if(B == null ) return 0;
int sum = 0;
Map.Entry aEntry = null;
Iterator> iter = B.entrySet().iterator();
while(iter.hasNext()){
aEntry = iter.next();
sum += aEntry.getValue();
}
return sum;
}
public static void main(String[] args) {
int[] coinValue = new int[] { 50, 20, 11, 5, 2,1 };
int money = 23;
changeCoins(coinValue, money);
}
}