初识Python数据可视化（二）

基于上一篇文章的基础，在本篇，我们将使用更多的数据来绘图。

• 点击查看上一篇文章：初识Python数据可视化（一）

通过Python生成模拟随机游走数据，然后使用matplotlib为模拟数据创建视觉上吸引人的表示形式。

随机游走是一条没有明确方向但由一系列随机决策确定的路径，每个决策都具有绝对的偶然性。

您可以想象成一只失去理智的蚂蚁，朝随机方向迈出的每一步时所走的路径。

随机游走在自然，物理学，生物学，化学和经济学中都有实际应用。我们将要编写的代码可以模拟许多实际情况。

---

创建一个随机游走的类

from random import choice


class RandomWalk():
    """生成随机游走的类"""

    def __init__(self, num_points=5000):
        """初始化步行属性"""
        self.num_points = num_points

        # 所有游走都从 (0, 0)点开始
        self.x_values = [0]
        self.y_values = [0]

    def fill_walk(self):
        """计算所有随机游走的点"""

        # 一直随机游走直到到达指定次数
        while len(self.x_values) < self.num_points:
            # 确定要去的方向以及该方向要走多远。
            x_direction = choice([1, -1])
            x_distance = choice([0, 1, 2, 3, 4])
            x_step = x_direction * x_distance

            y_direction = choice([1, -1])
            y_distance = choice([0, 1, 2, 3, 4])
            y_step = y_direction * y_distance
            # 判断是否移动
            if x_step == 0 and y_step == 0:
                continue

            # 计算下一步的x和y的值
            next_x = self.x_values[-1] + x_step
            next_y = self.y_values[-1] + y_step
            self.x_values.append(next_x)
            self.y_values.append(next_y)

在第15行，建立了一个循环，直到移动到达指定次数为止。

该方法的主要部分告诉Python如何模拟四个随机决策：

• 游走会向右还是向左？
• 朝那个方向走多远？
• 它会上升还是下降？
• 朝那个方向走多远？

第21行，我们使用choice([1, -1])为x选择一个方向值，若为1，则向右移动；否则，向左移动。

接下来，choice([0, 1, 2, 3 4])通过随机选择一个介于0和4之间的整数来告诉Python在向指定方向上移动多远。

通过将移动方向乘以所选的距离来确定x和y方向上每一步的长度。

x_step的正结果将我们向右移动，负结果将我们向左移动，0将我们垂直移动。

y_step的正结果表示向上移动，负值表示向下移动，0表示水平移动。

如果x_step和y_step的值都为0，则相对上一次未行走，我们通过第29行来判断以防止出现此情况。

为了获得行走的下一个x的值，我们将x_values中的最后一个值和x_step相加，并将结果添加到x_values。y同理。

---

绘制随机游走

import matplotlib.pyplot as plt
from random_walk import RandomWalk

# 创建随机游走，并绘制点
rw = RandomWalk()
rw.fill_walk()

plt.scatter(rw.x_values, rw.y_values, s=15)
plt.show()

我们首先导入pyplot和Randomwalk。

然后，我们创建一个随机游走对象并将其存储在rw中，并调用fill_walk()。

在第8行，我们将步行的x和y值输入scatter()并选择适当的点大小。

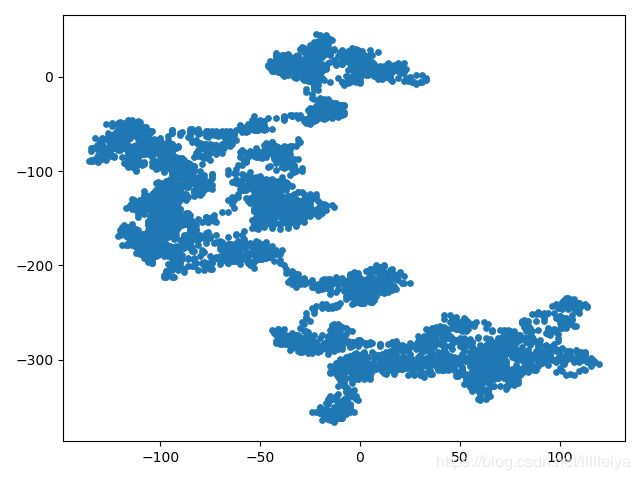
运行结果显示了具有5000个点的结果图。

代码运行结果：

生成多个随机游走

每次模拟随机行走都是不同的，使用while方法使前面的代码进行多次遍历而无需多次运行。

import matplotlib.pyplot as plt
from random_walk import RandomWalk

while True:
    rw = RandomWalk()
    rw.fill_walk()
    plt.scatter(rw.x_values, rw.y_values, s=15)
    plt.show()

    keep_running = input("绘制另一个随机行走? (y/n): ")
    if keep_running == 'n':
        break

装饰随机行走

我们将自定义图，以强调每次行走的重要特征，并不再强调干扰因素。

为此，我们确定要强调的特征，例如步行的起点，终点和走的路。

接下来，我们确定要强调的特征，例如刻度线和标签。结果应该是一个简单的视觉表示，可以清楚地传达每次随机行走所经过的路径。

给点着色

我们将使用色图显示步行中各点的顺序，然后从每个点中删除黑色轮廓，以便使点的颜色更清晰。

要根据步行中的位置为点着色，我们向参数c传递一个包含每个点位置的列表。因为这些点是按顺序绘制的，所以列表仅包含从1到5000的数字，如下所示：

import matplotlib.pyplot as plt
from random_walk import RandomWalk

while True:
    rw = RandomWalk()
    rw.fill_walk()
    point_numbers = list(range(rw.num_points))
    plt.scatter(rw.x_values, rw.y_values, c=point_numbers, cmap=plt.cm.Blues, edgecolor='none', s=15)
    plt.show()

    keep_running = input("绘制另一个随机行走? (y/n): ")
    if keep_running == 'n':
        break

第7行，我们使用range()生成一个数字列表，该数字列表等于步行中的点数。

然后，将它们存储在列表点编号中，我们将使用它们来设置步行中每个点的颜色。

我们将点号传递给参数c，使用Blues颜色图，然后传递edgecolor = 'none'消除每个点周围的黑色轮廓。

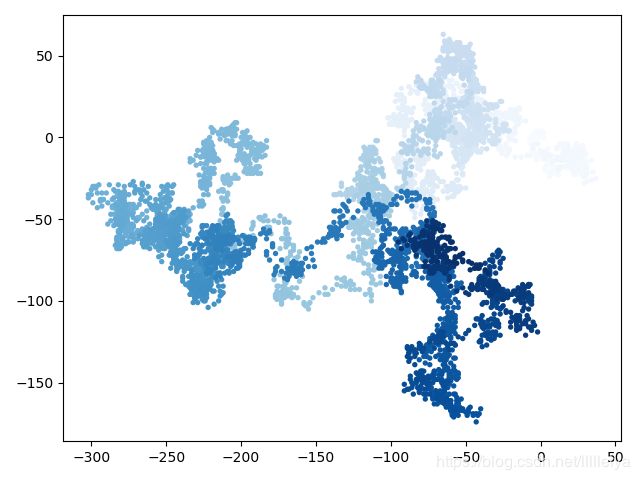
结果是沿着浅梯度从浅到深蓝色变化的行走曲线图。

代码运行结果之一：

绘制起点和终点

既然是模拟随机行走，起点和终点也是我们想要突出表现的元素。

我们可以分别绘制第一个和最后一个点。我们将使端点更大，并对端点进行着色以使其突出。

import matplotlib.pyplot as plt
from random_walk import RandomWalk

while True:
    rw = RandomWalk()
    rw.fill_walk()
    point_numbers = list(range(rw.num_points))
    plt.scatter(rw.x_values, rw.y_values, c=point_numbers, cmap=plt.cm.Blues, edgecolor='none', s=15)

    # 强调第一点和最后一点
    plt.scatter(0, 0, c='green', edgecolors='none', s=100)
    plt.scatter(rw.x_values[-1], rw.y_values[-1], c='red', edgecolors='none', s=100)

    plt.show()

    keep_running = input("绘制另一个随机行走? (y/n): ")
    if keep_running == 'n':
        break

因为我们的默认起始点为(0, 0)点。所以在第11行，对(0, 0)点单独进行修改，颜色设置为绿色，s设置为100。

同理，通过获取x_values和y_values的最后一个值即可得到终点，并单独对其进行修改，颜色设置为红色，s设置为100。

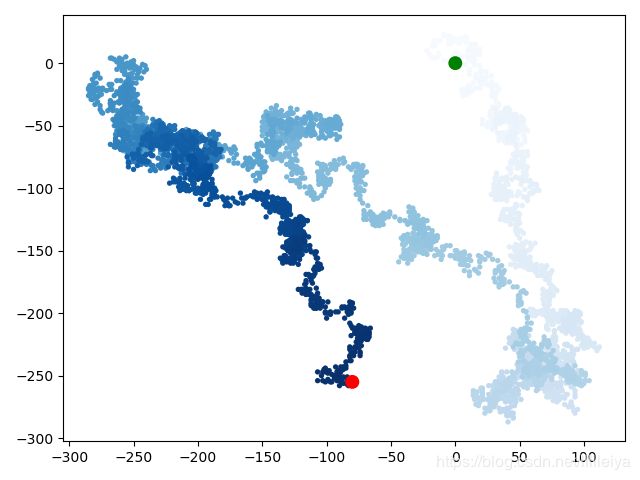
在运行结果中可以很明显的观察到模拟随机行走的起点和终点。

代码运行结果之一：

取消显示轴

为了避免每次观察图片时我们被轴所吸引，我们可以取消显示轴。

import matplotlib.pyplot as plt
from random_walk import RandomWalk

while True:
    rw = RandomWalk()
    rw.fill_walk()
    point_numbers = list(range(rw.num_points))
    plt.scatter(rw.x_values, rw.y_values, c=point_numbers, cmap=plt.cm.Blues, edgecolor='none', s=15)
    plt.scatter(0, 0, c='green', edgecolors='none', s=100)
    plt.scatter(rw.x_values[-1], rw.y_values[-1], c='red', edgecolors='none', s=100)

    # 去除轴
    plt.axes().get_xaxis().set_visible(False)
    plt.axes().get_yaxis().set_visible(False)

    plt.show()

    keep_running = input("绘制另一个随机行走? (y/n): ")
    if keep_running == 'n':
        break

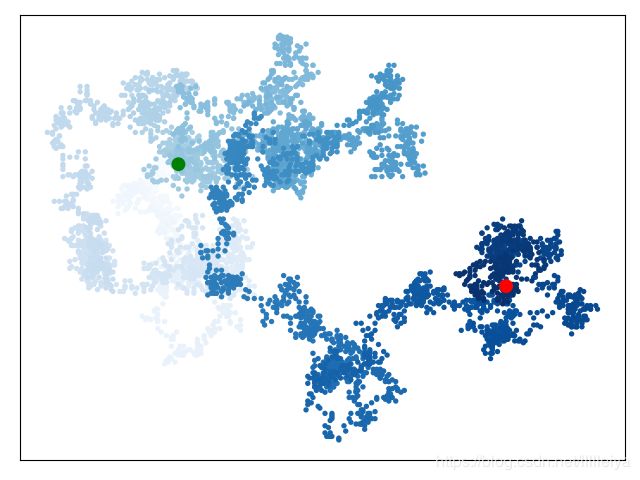
使用函数plt.axes()修改轴，将每个轴的set_visible设置为False。

代码运行结果之一：

---

增加绘图点

让我们增加点数，以便为我们提供更多数据。

为此，我们在创建Randomlalk实例时增加num points的值，并在绘制图时调整每个点的大小。

import matplotlib.pyplot as plt
from random_walk import RandomWalk

while True:
    rw = RandomWalk(50000)
    rw.fill_walk()
    point_numbers = list(range(rw.num_points))
    plt.scatter(rw.x_values, rw.y_values, c=point_numbers, cmap=plt.cm.Blues, edgecolor='none', s=1)
    plt.scatter(0, 0, c='green', edgecolors='none', s=100)
    plt.scatter(rw.x_values[-1], rw.y_values[-1], c='red', edgecolors='none', s=100)

    # 去除轴
    plt.axes().get_xaxis().set_visible(False)
    plt.axes().get_yaxis().set_visible(False)

    plt.show()

    keep_running = input("绘制另一个随机行走? (y/n): ")
    if keep_running == 'n':
        break

本示例创建一个具有50,000个点的随机游走（以反映真实世界的数据），并以s = 1的大小绘制每个点。

代码运行结果之一：

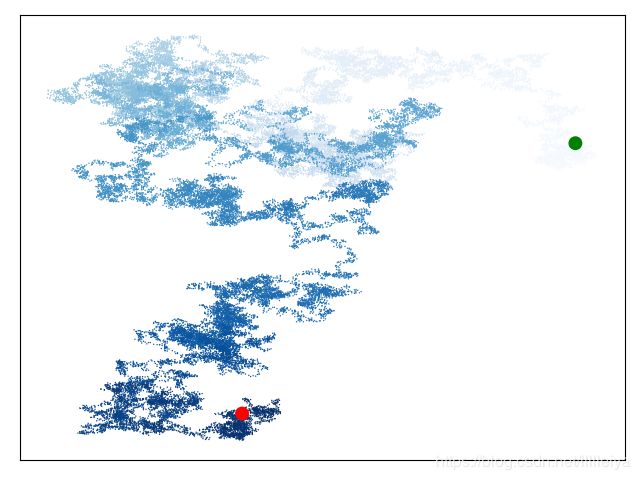
观察运行结果，由此产生的步态非常小巧，并且形状类似云。

如您所见，我们已经通过一个简单的散点图创建了一件艺术品！

可以根据你的电脑性能增加步数。并再次尝试使用此代码。

更改大小以填充屏幕

如果可视化图像大小非常适合屏幕显示，则可视化将更有效地传达数据模式。

为了使绘图窗口更好地适合您的屏幕，请调整matplotlib输出的大小。

import matplotlib.pyplot as plt
from random_walk import RandomWalk

while True:
    rw = RandomWalk(50000)
    rw.fill_walk()

    # 设置绘图窗口的大小
    plt.figure(figsize=(10, 6))

    point_numbers = list(range(rw.num_points))
    plt.scatter(rw.x_values, rw.y_values, c=point_numbers, cmap=plt.cm.Blues, edgecolor='none', s=1)
    plt.scatter(0, 0, c='green', edgecolors='none', s=100)
    plt.scatter(rw.x_values[-1], rw.y_values[-1], c='red', edgecolors='none', s=100)

    # 去除轴
    plt.axes().get_xaxis().set_visible(False)
    plt.axes().get_yaxis().set_visible(False)

    plt.show()

    keep_running = input("绘制另一个随机行走? (y/n): ")
    if keep_running == 'n':
        break

figure()函数控制绘图的宽度，高度，分辨率和背景色。参数figsize接收一个元组，该元组告诉matplotlib绘图窗口的尺寸（以英寸为单位）。
代码运行结果之一：

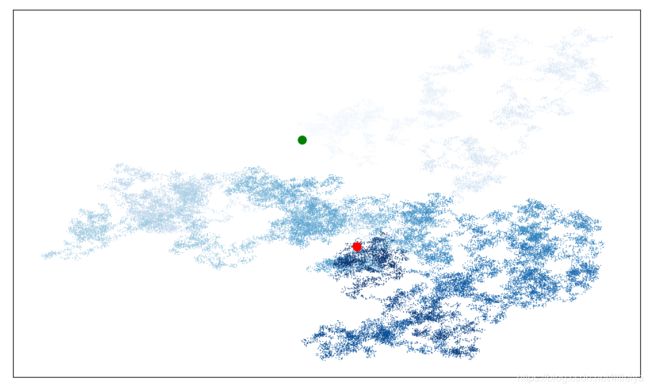
Python假定您的屏幕分辨率为每英寸80像素

• 如果此代码不能为您提供准确的绘图大小，请根据需要调整数字;
• 如果您知道系统的分辨率，请使用参数dpi传递figure()分辨率以设置有效利用空间的绘图大小在屏幕上可用

plt.figure(dpi=128, figsize=(10, 6))