【机器学习】这份分类决策树算法介绍请收好！

摘要： 决策树在机器学习算法中是一个相对简单的算法，如何不能进行适当的剪枝就容易造成模型的过拟合。决策树算法也是当前很多集成学习算法的基础，集成算法的效果往往比单独使用决策树算法效果更好。

关键词： 决策树，集成学习

1 初识决策树

决策树就是一个根据原始数据的特征的重要性逐渐确定数据的类别的一种算法。之所以被称为决策树，是因为训练的模型根据训练的数据确定特征的重要性，然后对测试数据分析时会根据不同数据的各个特征值一步一步地分析到分类，就如同一棵树从树根到树叶的路径一样，可参考下图：

决策树传统上来讲主要是用来做分类的，但是也不排除可以使用该算法进行回归分析，之前的文章也有过介绍如：【机器学习】分类算法其实也可做回归分析——以knn为例。本文主要介绍使用决策树进行分类的原理。

2 构造决策树

刚才说到，决策树是根据数据的不同重要的特征进行一步一步地划分数据的，那么使用什么指标来确定特征的重要性呢？当前主要使用的衡量指标是信息熵和基尼(Gini)指数。

2.1 通过熵构建决策树

2.1.1 信息熵

文献1中指出，信息熵是衡量信息不确定性的指标，不确定性是一个事件出现不同结果的可能性。对应的计算公式如下：
$$H\left(Y\right)=-\sum _{i=1}^{n}P\left(y_i\right){\log }_{2}P\left(y_i\right)$$
其中，$y_i$是随机变量$Y$的一个可能事件，$P(y_i)$则代表该事件发生的概率。以常见的例掷硬币为例，两枚骰子正反面出现的概率如下：

硬币	概率
正面	0.5
反面	0.5

对于该硬币掷出去后，信息熵如下：
$$H\left(Y\right)=-0.5\times {\log }_{2}0.5-0.5\times {\log }_{2}0.5=1$$

硬币	概率
正面	0.99
反面	0.01

同理，对于该硬币掷出去后，信息熵如下：
$$H\left(Y\right)=-0.99\times {\log }_{2}0.99-0.0.1\times {\log }_{2}0.01=0.08$$
从上面的例子我们可以看出，第二枚硬币正面的概率为0.99，我们基本可以认为硬币掷出去后是正面，所有信息熵比较小，而对于第一枚硬币，由于正反面概率相同，这时掷出硬币后就比较难确定正反面了，信息熵也就比较大了。

2.1.2 条件熵

在决策树确定特征的重要性时除了信息熵以外，还会用到条件熵。在给定随机变量$X$的条件下，随机变量$Y$的不确定性。公式如下：
$$H\left(Y|X\right)=-\sum _{i=1}^{n}P\left(y_i|x_i\right){\log }_2\left(y_i|x_i\right)$$
其中$x_i$和$y_i$分别是随机变量$X$、$Y$的一个事件。

2.1.3 信息增益

信息增益的定义就是：事件的熵值减去对应的条件熵，代表了在一个条件下，信息不确定性减少的程度。通过下面的公式就可以了解。
$$I\left(X,Y\right)=H\left(Y\right)-H\left(Y|X\right)$$
当信息增益越大，那么在这个条件下知晓后，事件就比较容易确定了。计算案例可以参考如下（知道某个条件后分成将原始数据分成了两堆）：

2.1.4 决策树结构过程

有以下数据，该数据是在不同天气情况下客户打高尔夫球的记录。每条数据包含Outlook、Temp、Humanity、Wind四个特征以及对应的数据标签是否Play Golf。现在我们就可以通过结合天气信息较少不确定性来判断在一些情况下客户是否会打Golf。而每个特征都有多个取值。

现在我们需要明确研究对象，即是否打Golf。
第一步就是：计算Play Golf的熵，可以根据下表进行计算：

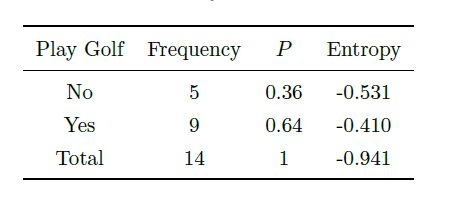
首先是构建根节点，先看Play Golf 的熵：在14 条历史数据中，打球的概率为0.64，不打球的
概率为0.36，熵值为0.94。
第二步就是：寻找晴朗程度、湿度、风力和温度四种状况与是否打高尔夫相关性最高的一个特征，进行决策树构建。

1. 以Outlook为条件计算的条件熵和信息增益如下：
   
   
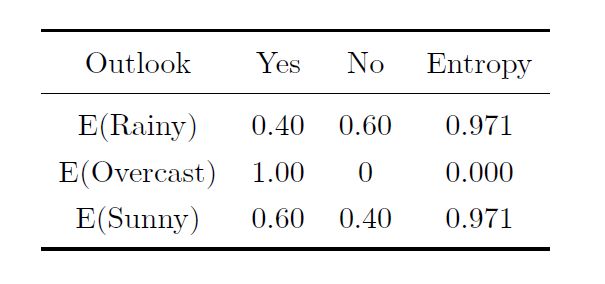
   那么使用Outlook的条件熵：
   $$0.36\times 0.971+0.29\times 0+0.36\times 0.971=0.69$$
   信息增益：0.940-0.69=0.25 (最佳分割特征)
2. 同理分别以Temp、Humidity、Wind计算出对应的信息增益结果为：0.02，0.15，0.05.
3. 经比较Outlook的信息增益最大，将其设置为第一个分类依据特征，根据Outlook的取值就可以构建如下图的树：
   
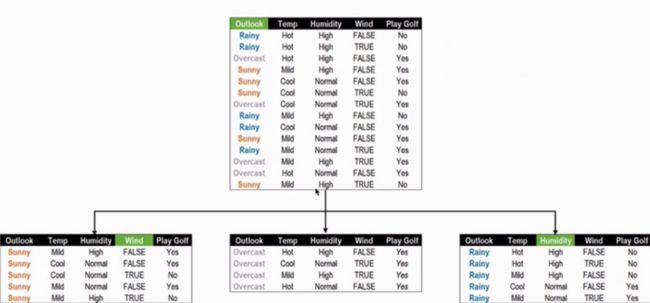
   根据上图结果可以看出在Outlook为Overcast时，这时全部是Play Golf，进而可将决策树简化为下图：
   
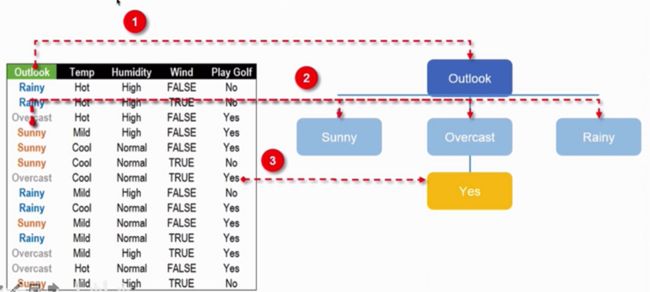
   但是在Sunny和Rainy这两个分支中还有数据需要继续划分，划分时只用考虑Temp、Humidity、Wind这三个特征。
   在Sunny枝节上的划分时，如下图：
   
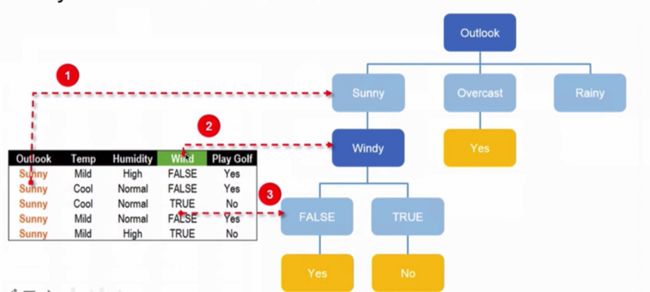
   从图中可以看出在Wind特征中，只要是False就Play Golf，True就不打Golf， 也就是说可以对剩下的数据进行划分了，这个枝节结束。当然，同样可以使用信息增益的方式确定这三个特征的优先级。

在Rainy枝节上的划分时，如下图：

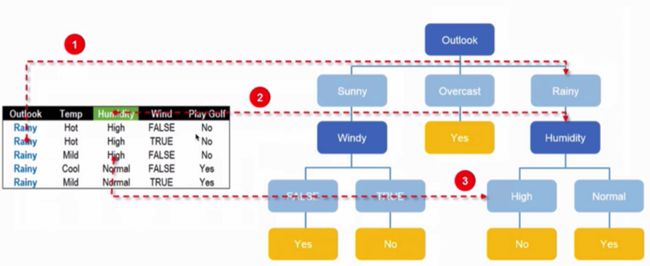
从图中可以看出在Humidity特征中，只要是Normal就Play Golf，High就不打Golf，同样也可以使用信息增益的方式选择该特征。另一方面说，这时针对训练数据，决策树就构建完成了。

2.1.5 决策树模型数据预测

假设我们有一个数据如下：

Outlook	Temp	Humidity	Wind	Play Golf
Sunny	Mild	High	False	?

那么根据刚刚构建的决策树模型，则有下图：

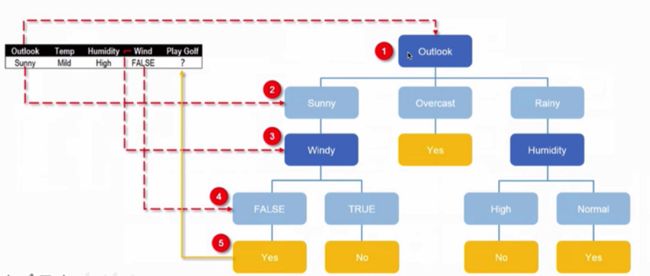
那么就可以预测出“True”，即去打Golf。以这种方式构建决策树的算法称为ID3决策树生成算法。

2.2 基于基尼指数构建决策树

使用基尼指数去确定数据的特征的重要性。根据文献1介绍，基尼指数(Gini不纯度)表示在样本集合中一个随机选中的样本被分错的概率。
注：Gini指数越小表示集合中被选中的样本被分错的概率越小，也就是说集合的纯度越高，反之集合就不纯。当集合中所有样本为一个类时，基尼指数为0.
在当前特征条件下，对于是否打Golf，当基尼指数越小时那么，那么集合纯度越大，其对应的特征就越重要。
根据文献2基尼指数定义如下：分类问题中，假设有K个类，样本点属于第k类的概率为$p_k$，则概率分布的基尼指数如下：
$$Gini\left(p\right)=\sum _{k=1}^K{p}_k\left(1-p_k\right)=1-\sum _{k=1}^K{p}_k^2$$
使用基尼指数的方式与信息熵相同，使用基尼增益确定哪个特征的重要性，下面来看一个例子。

2.2.1 使用基尼指数构建决策树

依然使用根据天气预测是否打高尔夫球的案例，数据在2.1.4节。
根据原始数据计算基尼不纯度，一个14条数据，5次No，9次Yes，则基尼不纯度为：
$$Gini=1-{\left(\frac{5}{14}\right)}^2-{\left(\frac{9}{14}\right)}^2=0.459$$
以Outlook特征为条件的基尼指数计算，这时Outlook特征不同取值的概率就可看成一个权重，而Outlook一个取值下存在Play Golf和不打Golf，那么在这个特征下加权的基尼不纯度为：
$$\begin{array}{rl}Gini& =\left(5/14\right)\times gini\left(2,3\right)+\left(4/14\right)\times gini\left(4,0\right)+\left(5/14\right)\times gini\left(3,2\right)\\ & =5/14\times (1-(2/5{)}^2-(3/5{)}^2)+(4/14)\times (1-(4/4{)}^2)+\\ & +5/14\times (1-(3/5{)}^2-(2/5{)}^2)=0.342\end{array}$$
注：gini(a,b)表示，在当前条件两种结果出现的次数a,b下的基尼指数。
进而可以计算出Gini增益为：0.459-0.342=0.117
同理可计算出分别以Temp，Wind，Humidity为条件的特征的基尼增益为：0.0185，0.0304，0.0916。经比较Outlook的基尼增益最大，特征最重要，与使用熵的方式相类似，以此类推就可以构建一个决策树了。

2.3 基于信息增益比构建决策树

由于以信息增益作为划分训练数据集特征，存在偏向于选择取值较多的问题。使用信息增益比可以对这一问题进行校正。
根据文献2，可知信息增益比：特征A对训练数据集D的信息增益比为：其信息增益$g(D,A)$与训练数据集D关于特征A的值的熵$H_A(D)$之比。其中$H_A(D)$公式如下：
$$H_A\left(D\right)=-\sum _{i=1}^n\frac{|D_i|}{|D|}{\log }_2\frac{|D_i|}{|D|}$$
这里的n表示特征A取值的个数。以这种方式构建决策树的算法称为C4.5决策树生成算法。

Reference

[1] 集成学习：XGBoost, lightGBM. https://www.bilibili.com/video/BV1Ca4y1t7DS
[2] 李航.统计学习方法[M]. 北京，清华大学出版社:55-75