【机器学习】回归树分析与sklearn决策树案例！

摘要： 决策树是非常基础的算法，其不仅能够进行分类还可以进行回归处理，也就是回归树。要想提高决策树的性能还需要做好剪枝的工作。

关键词： 回归树，剪枝

1 回归树

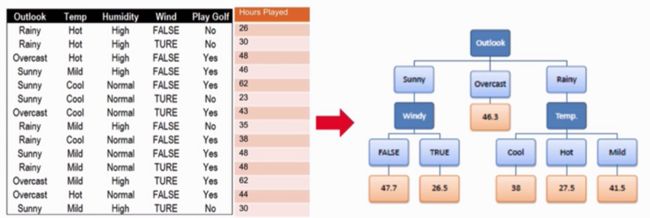
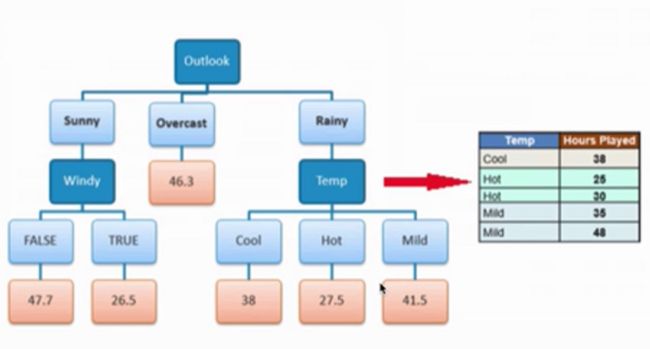
之前已经介绍过决策树的基本理论了：【机器学习】这份分类决策树算法介绍请收好！。回归树（regression tree），顾名思义是将决策树应用于回归问题当中的，直接也介绍过如何使用knn算法做回归分析。现在看看如何使用树模型来进行回归分析。使用决策树做回归时，树的叶子节点就不再是类别了，而是叶子节点所含训练集元素输出的均值，如下图。（这里Play Golf姑且看成一个特征，每条数据都是去打golf的，就是每次打的时间不一样），模型目标变为预测打高尔夫时间。

本部分内容主要参考文献1和文献2。

在分类决策树中在进行树分叉特征选择的时候使用的是熵或者基尼指数。回归树则有所不同，使用的方式可选在某个特征条件下的数据的标准差来确定。回归树根据数据特征将样本分为很多个集合，然后再根据集合中的数据的标准方差来衡量这些元素是否相近，如果不相近的话，再继续分。根据上图打高尔夫球时间数据对于根节点有，
$$\begin{gathered} 1.Count=n=14 \\ 2.Aveage=\hat{x}=\frac{\sum x}{n}=39.8 \\ 3.standardDeviation=S=\sqrt{\frac{\sum (x-\bar{x}{)}^2}{n}}=9.32 \\ 4.CoeffeicientofVariation=CV=\frac{S}{\bar{x}}\times 100\%=23\% \end{gathered}$$
注释：
1.数据集元素个数
2.数据集样本标签的均值，如果为叶子节点，那么就是预测值
3.标准方法衡量集合中元素的相似度
4.变化系数用于决定是否停止进一步分叉

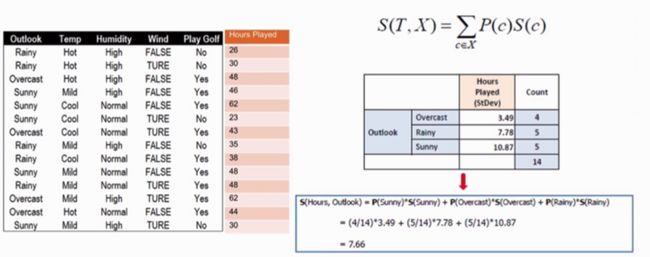
以计算Outlook分支后的标准差为例，则条件标准方法如下：
$$S\left(T,X\right)=\sum _{c\in \text{X}}P\left(c\right)S\left(c\right)$$
P( c)指每个特征所占的比例，S( c)表示这个特征下数据的标准方。计算示意图如下：

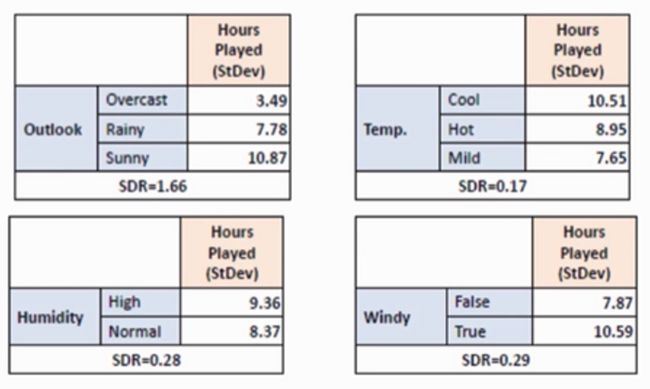
同理可以使用其他特征Temp、Humidity、Windy，计算得到的条件标准差结果如下图：

借用之前使用决策树进行分类的方法使用信息增益来确定特征重要性的思想，接下来使用方差减小值得特征。SDR公式如下：
$$SDR\left(T,X\right)=S\left(T\right)-S\left(T,X\right)$$
从上图可以比较出Outlook特征的SDR最大为1.66，那么就使用Outlook进行分支。分支后的图如下：

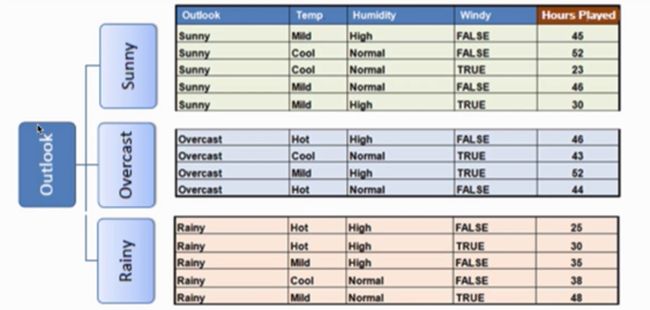
接下来就重复上面的过程，使用标准方法降低最多的特征进行分支，直到满足某个停止条件，如：1.当某个分支的变化系数小于某个值(10%)，2.当前节点包含的元素个数小于某个值(3)。
使用“outlook”分支以后，有如下表：

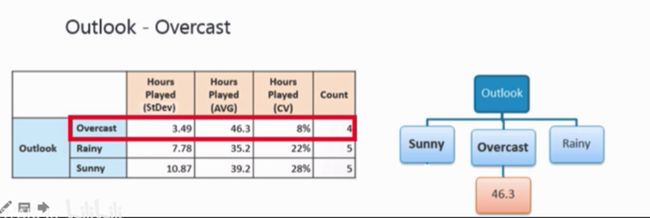值为“Overcast”的分支变化系数(coefficient of variation)为8%，小于设定的10%，则在Overcast下停止分支，即生成一个叶子节点。叶子节点的值就是当前叶子节点中包含数据的均值。

下面我们再看Outlook为Sunny后，其他几个特征的情况。根据上表的计算，Sunny分支的变化系数还大于10%，那么也还需要分支。这时再比较另外的特征即可，如下图：

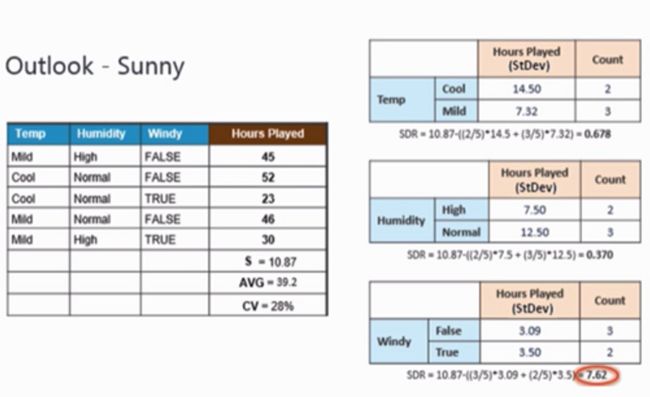
这时可以看到“Windy”特征的“增益”最大，使用这个特征继续分支，如下：

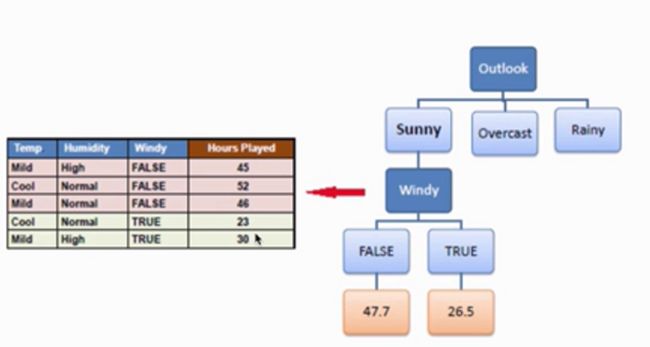
“Windy”特征可取两个值，这两个值下的数据集数量都不足3，则都停止分支，得到结果。
下面我们再继续看Outlook为Rainy后，其他几个特征的情况。

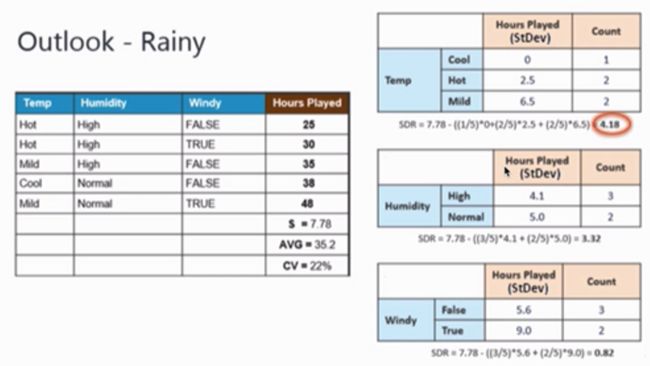
同理找出决策特征为“Temp”。由于Temp特征可取三个值，而每个值下对应的数据个数不超过3，则不需进行下一步的分支，结果如下：

2 决策树的优化

不管是分类决策树，还是树回归。我们可以看到在进行分支时如果不进行限定，构造的决策树直到所有的叶结点都是纯的叶结点，就会导致模型非常复杂，在训练集上正确率达到百分百，与此同时模型也会高度过拟合。为了防止过拟合，两种常见的策略如下：
1.及早停止树的生长，也叫预剪枝(pre-pruning)
2.先构造决策树，但随后删除或折叠信息量很少的节点，也叫后剪枝(post-pruning)
根据上面的策略我们可以使用限定决策树深度、叶子节点数据集个数等指标来剪枝。更多的理论介绍可以参见文献2，其中还介绍了损失函数等内容，这里不再介绍。

3 使用scikit-learn构建决策树

本实验环境为：Python3.7， sklearn 0.22.1
导数机器学习相关包：

from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split

模型训练和数据预测：

# 加载数据集
cancer_data = load_breast_cancer()
# 数据集分割
X_train, X_test, y_train, y_test = train_test_split(cancer_data.data, cancer_data.target, stratify=cancer_data.target, random_state=2)
# 构建分类决策树模型
tree = DecisionTreeClassifier(random_state=0) # 默认将树完全展开，random_state=0，用于解决内部平局问题
# 模型训练
tree.fit(X_train, y_train)

得到的模型如下：

DecisionTreeClassifier(ccp_alpha=0.0, class_weight=None, criterion='gini',
                       max_depth=None, max_features=None, max_leaf_nodes=None,
                       min_impurity_decrease=0.0, min_impurity_split=None,
                       min_samples_leaf=1, min_samples_split=2,
                       min_weight_fraction_leaf=0.0, presort='deprecated',
                       random_state=0, splitter='best')

模型在训练数据和测试数据上预测的结果如下：

# 模型结果查看
print("Accuracy on training set:{:.3f}".format(tree.score(X_train,y_train)))
print("Accuracy on test set:{:.3f}".format(tree.score(X_test,y_test)))
"""
Accuracy on training set:1.000
Accuracy on test set:0.916
"""

在训练数据上模型的正确率为100%，很明显，模型过拟合了。
下面，通过限制决策树的深度max_depth来减少过拟合，从而提高测试集的精度。

tree = DecisionTreeClassifier(max_depth=4, random_state=0)
tree.fit(X_train, y_train)
# 模型结果查看
print("Accuracy on training set:{:.3f}".format(tree.score(X_train,y_train)))
print("Accuracy on test set:{:.3f}".format(tree.score(X_test,y_test)))
"""
Accuracy on training set:0.988
Accuracy on test set:0.958
"""

从结果可以看出，虽然训练集中的正确率有所降低，但测试集中的正确率就得到了提高，也说明这种方法有降低模型过拟合的效果。

下面结合graphviz来可视化句法树，相关环境的配置可参见：【Tools】一个绘制决策树的工具——graphviz，但你忽视了它的其他功能！ 。当然需要使用scikit-learn中树模型的export_graphviz模型导出graphviz自动化绘制的.dot格式文件。操作如下：
生成dot格式文件

from sklearn.tree import export_graphviz

export_graphviz(tree, out_file='tree.dot', class_names=["malignant", "benign"], 
feature_names=cancer_data.feature_names, impurity=False, filled=True)

绘制决策树

import graphviz
with open("tree.dot") as f:
    dot_graph = f.read()
# 使用计算机自带软件打开决策树
# dot = graphviz.Source(dot_graph, format="pdf")  # 保存到pdf矢量图
# dot.view()  
# 页面直接显示
graphviz.Source(dot_graph)

结果如下：

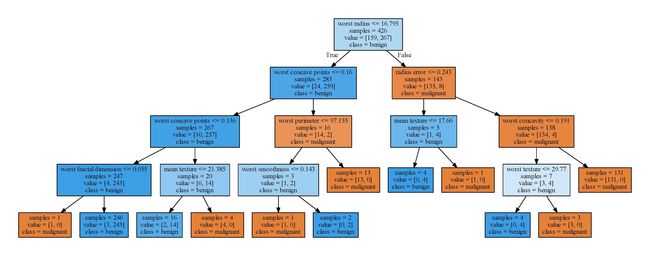
树的可视化有助于深入理解算法是如何预测的。从树的结果也可以更加容易地分析出数据的特征。上面的树层数只有4，当然也会有更大。上图的决策树绘制结果还能够清晰地看出各个特征下数据的样本数，样本中的值以及分类等。
除了绘制出决策树查看结果，我们也可以从模型中输出这个结构树的重要特征属性，模型会默认就数据的特征进行排序。如下：

print("Feature importance:\n{}".format(tree.feature_importances_))
"""
Feature importance:
[0.         0.0342316  0.         0.         0.         0.
 0.         0.         0.         0.         0.03021217 0.
 0.         0.         0.         0.         0.         0.
 0.         0.         0.73874761 0.01805623 0.01141053 0.
 0.00702187 0.         0.02285378 0.12723034 0.         0.01023586]
"""

对于每个特征来说，在这个输出中，都是介于0和1之间的数字，其中0表示“根本没有用到”，1表示“完美预测目标值”，并且重要性的求和是1.可视化如下：

import numpy as np
import matplotlib.pyplot as plt
def plot_feature_importances_cancer(model):
    n_features = cancer_data.data.shape[1]
    # 绘制水平柱状图
    plt.barh(range(n_features), model.feature_importances_, align='center')
    plt.yticks(np.arange(n_features), cancer_data.feature_names)
    plt.xlabel('Feature importance')
    plt.ylabel('Feature')

plot_feature_importances_cancer(tree)

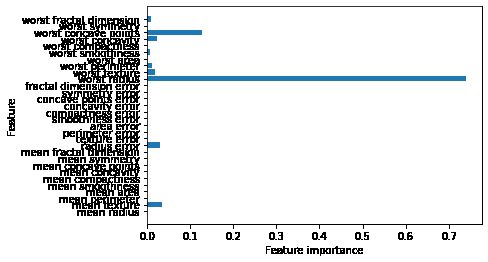
从图中可以看出有些特征没有用上，但这并不能说明该特征没有提供任何信息，只能说明该特征没有被树选中，可能是因为另一个特征包含了同样的信息。

总结

决策树的模型容易可视化，非专家也很容易理解，算法完全不受数据缩放的影响。但是想提高决策树算法的性能，需要做好剪枝的操作，选择一种策略（max_depth,max_leaf_nodes,min_samples_leaf）防止模型过拟合。但是，即使做了预剪枝模型还是容易过拟合，泛化性能差。在实际的大多数应用中往往会使用集成方法来替代单颗决策树。

Reference

[1] 集成学习：XGBoost, lightGBM. https://www.bilibili.com/video/BV1Ca4y1t7DS
[2] 李航.统计学习方法[M]. 北京，清华大学出版社:55-75