频域分析之超前校正
本文将主要介绍使用频域响应法进行控制器设计时一种常用且重要的方法–超前校正
超前校正能使系统的瞬态响应得到显著改善,而对系统稳态精度的影响则很小。
首先来看超前校正的一般形式
K c α T s + 1 α T s + 1 = K c s + 1 T s + 1 α T ( 0 < α < 1 ) K_{c} \alpha \frac{T s+1}{\alpha T s+1}=K_{c} \frac{s+\frac{1}{T}}{s+\frac{1}{\alpha T}} \quad(0<\alpha<1) KcααTs+1Ts+1=Kcs+αT1s+T1(0<α<1)
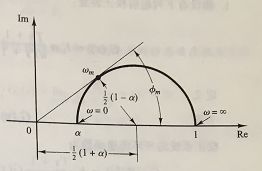
可以看出,其零点位于 s = − 1 / T s=-1 / T s=−1/T,极点位于 s = − / ( α T ) s=-/(\alpha T) s=−/(αT),所以在复平面,零点总是位于极点的右方。值得注意的是 α \alpha α最小值受到超前校正物理结构的限制,通常取0.05左右,这也意味着,超前校正装置可以产生的最大相角超前为 6 5 ∘ 65^{\circ} 65∘。
绘制出超前校正传递函数的奈奎斯特曲线(图中 K c = 1 K_c=1 Kc=1)
K c α j ω T + 1 j ω α T + 1 K_{c} \alpha \frac{j \omega T+1}{j \omega \alpha T+1} KcαjωαT+1jωT+1
可以看出超前校正可以产生的最大相角超前为
sin ϕ m = 1 − α 2 1 + α 2 = 1 − α 1 + α \sin \phi_{m}=\frac{\frac{1-\alpha}{2}}{\frac{1+\alpha}{2}}=\frac{1-\alpha}{1+\alpha} sinϕm=21+α21−α=1+α1−α
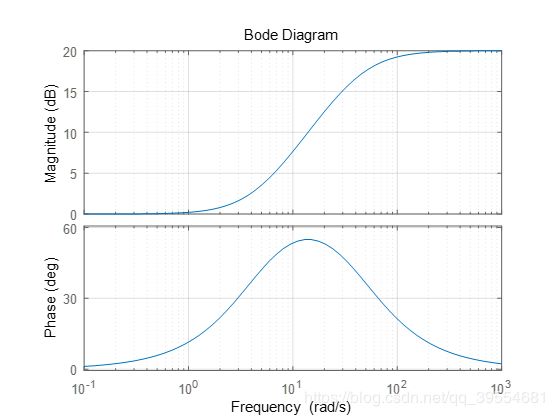
绘出超前校正系统的bode图:(图中 K c = 10 , a l p h a = 0.1 , T = 0.2 K_c=10,alpha=0.1,T=0.2 Kc=10,alpha=0.1,T=0.2)
可以看出系统的低频幅值趋近于 20 l g ( K c α ) 20lg(K_c \alpha) 20lg(Kcα),高频幅值趋近于 20 l g ( K c ) 20lg(K_c) 20lg(Kc);
最大超前相角处的频率值为
log ω m = 1 2 ( log 1 T + log 1 α T ) \log \omega_{m}=\frac{1}{2}\left(\log \frac{1}{T}+\log \frac{1}{\alpha T}\right) logωm=21(logT1+logαT1)
即
ω m = 1 α T \omega_{m}=\frac{1}{\sqrt{\alpha} T} ωm=αT1
对应了两个转角频率的几何中心。
重要:
可以看出,通过合适地选取参数,超前校正环节在中频段为系统带来了超前相角,同时中频段的斜率增加了 + 20 d B / 十 倍 频 程 +20dB/十倍频程 +20dB/十倍频程,这将使校正后的系统中频段的幅值下降地更缓,使得系统增益交接频率提高(幅值穿越频率),应当指出,带宽近似于增益交接频率;这意味着系统的闭环带宽增加,快速性会提高,动态性能得到改善,同时超前校正在增加系统穿越频率的同时,保证了系统的相角裕度不会大幅减小(超前校正产生足够大的相角超前,可以补偿原系统中的元件造成的过大的相角滞后)。
例子:
设系统的开环传递函数为 G ( s ) = s s ( s + 2 ) G(s)=\frac{s}{s(s+2)} G(s)=s(s+2)s,如果要使系统的静态速度误差常数 K v K_v Kv为 20 s − 1 20s^{-1} 20s−1,相位裕度不小于 5 0 ∘ 50^{\circ} 50∘,增益裕量不小于 10 d B 10dB 10dB,试设计一个系统校正装置。
我们采用如下形式的超前校正装置:
G c ( s ) = K c α T s + 1 α T s + 1 = K c s + 1 T s + 1 α T ( 0 < α < 1 ) G_c(s)=K_{c} \alpha \frac{T s+1}{\alpha T s+1}=K_{c} \frac{s+\frac{1}{T}}{s+\frac{1}{\alpha T}} \quad(0<\alpha<1) Gc(s)=KcααTs+1Ts+1=Kcs+αT1s+T1(0<α<1)
定义:
G 1 ( s ) = K G ( s ) = 4 K s ( s + 2 ) G_{1}(s)=K G(s)=\frac{4 K}{s(s+2)} G1(s)=KG(s)=s(s+2)4K
其中: K = K c α K=K_c \alpha K=Kcα
首先调整开环增益以满足系统的稳态误差指标;
K v = lim s → 0 s G c ( s ) G ( s ) = lim s → 0 s T s + 1 α T s + 1 G 1 ( s ) = lim s → 0 s 4 K s ( s + 2 ) = 2 K = 20 K_{v}=\lim _{s \rightarrow 0} s G_{c}(s) G(s)=\lim _{s \rightarrow 0} s \frac{T s+1}{\alpha T s+1} G_{1}(s)=\lim _{s \rightarrow 0} \frac{s 4 K}{s(s+2)}=2 K=20 Kv=s→0limsGc(s)G(s)=s→0limsαTs+1Ts+1G1(s)=s→0lims(s+2)s4K=2K=20
K = 10 K=10 K=10
当 K = 10 K=10 K=10时,已校正的系统将满足稳态要求。
绘制下列函数的波德图:
G 1 ( j ω ) = 40 j ω ( j ω + 2 ) = 20 j ω ( 0.5 j ω + 1 ) G_{1}(j \omega)=\frac{40}{j \omega(j \omega+2)}=\frac{20}{j \omega(0.5 j \omega+1)} G1(jω)=jω(jω+2)40=jω(0.5jω+1)20
相角裕度约为 1 7 ∘ 17^{\circ} 17∘,这意味着系统具有相当强烈的振荡(相角裕度越小超调越大);
需要补充的相位超前为 3 3 ∘ 33^{\circ} 33∘;
由于增加超前校正会使系统的增益交界频率向右移动,因此必须对交界频率增加造成的相位滞后进行补偿,故本设计中取需要增加的相位超前量为 3 8 ∘ 38^{\circ} 38∘;
根据
sin ϕ m = 1 − α 1 + α \sin \phi_{m}=\frac{1-\alpha}{1+\alpha} sinϕm=1+α1−α
得到
α = 0.24 \alpha=0.24 α=0.24
我们令产生最大超前相角时的频率为校正后系统的穿越频率,则有
∣ 1 + j ω T 1 + j ω α T ∣ ω = 1 / ( α T ) = ∣ 1 + j 1 α 1 + j α 1 α ∣ = 1 α \left|\frac{1+j \omega T}{1+j \omega \alpha T}\right|_{\omega=1 /(\sqrt{\alpha} T)}=\left|\frac{1+j \frac{1}{\sqrt{\alpha}}}{1+j \alpha \frac{1}{\sqrt{\alpha}}}\right|=\frac{1}{\sqrt{\alpha}} ∣∣∣∣1+jωαT1+jωT∣∣∣∣ω=1/(αT)=∣∣∣∣∣1+jαα11+jα1∣∣∣∣∣=α1
1 α = 1 0.24 = 1 0.49 = 6.2 d B \frac{1}{\sqrt{\alpha}}=\frac{1}{\sqrt{0.24}}=\frac{1}{0.49}=6.2 \mathrm{dB} α1=0.241=0.491=6.2dB
可知 G 1 ( s ) G_1(s) G1(s)在该频率处的幅值应为 − 6.2 d B -6.2dB −6.2dB,解出 ω = 9 r a d / s \omega =9rad/s ω=9rad/s,即为截止频率 ω c \omega_c ωc;
ω c = 1 / ( α T ) \omega_{c}=1 /(\sqrt{\alpha} T) ωc=1/(αT)
1 T = α ω c = 4.41 \frac{1}{T}=\sqrt{\alpha} \omega_{c}=4.41 T1=αωc=4.41
即
1 α T = ω c α = 18.4 \frac{1}{\alpha T}=\frac{\omega_{c}}{\sqrt{\alpha}}=18.4 αT1=αωc=18.4
因此,超前校正系统的传递函数为:
G c ( s ) = K c s + 4.41 s + 18.4 = K c α 0.227 s + 1 0.054 s + 1 G_{c}(s)=K_{c} \frac{s+4.41}{s+18.4}=K_{c} \alpha \frac{0.227 s+1}{0.054 s+1} Gc(s)=Kcs+18.4s+4.41=Kcα0.054s+10.227s+1
式中
K c = K α = 10 0.24 = 41.7 K_{c}=\frac{K}{\alpha}=\frac{10}{0.24}=41.7 Kc=αK=0.2410=41.7
则有
G c ( s ) = 41.7 s + 4.41 s + 18.4 = 10 0.227 s + 1 0.054 s + 1 G_{c}(s)=41.7 \frac{s+4.41}{s+18.4}=10 \frac{0.227 s+1}{0.054 s+1} Gc(s)=41.7s+18.4s+4.41=100.054s+10.227s+1
校正后系统的开环传递函数为:
G c ( s ) G ( s ) = 41.7 s + 4.41 s + 18.4 4 s ( s + 2 ) G_{c}(s) G(s)=41.7 \frac{s+4.41}{s+18.4} \frac{4}{s(s+2)} Gc(s)G(s)=41.7s+18.4s+4.41s(s+2)4
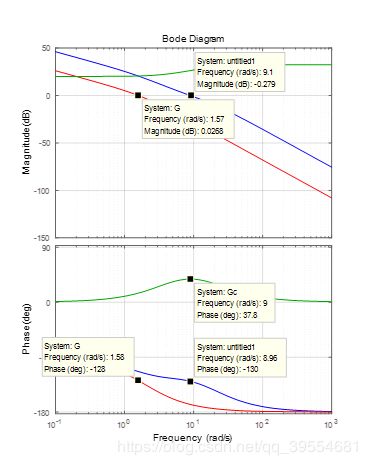
画出超前校正装置(绿),未校正系统(红),校正后系统(蓝)的波德图:
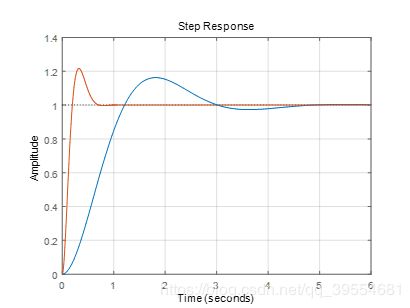
阶跃响应曲线如下:
可以看到动态性能变好,校正后系统相比原系统相角裕度略微减小,所以可以看到阶跃响应的超调量增加了。