概率和期望

（在此鸣谢yty提供故事的人物材料）

引子

概率是一个玄学的东西 。有个认知方面的误区就是，各位oier在小学和初中的时候接触到的概率都是一个叫做“古典概率”的东西，这是很只是概率这一个大旗帜下的一个小喽啰，真正的概率水深着呢。

先讲个故事吧（about Pascal & Fermat）by《数学一本通》

yty是hh的基友，有一天，yty跟hh说，他对赌博饥渴难耐，hh很无奈，只能陪yty进行了一场赌博。yty和hh下了相同的赌注，约定先获胜3局的那个人获得全部赌金。然后这俩家伙就开始了史诗级oier之间的赌博。yty赢了2局，hh赢了1局，这个时候，hh的GF（懂吧）突然给hh打了一个电话，说要hh陪吃饭，yty表示很无奈，被塞一口狗粮，没心思再赌博，就同意hh离开了。但是yty想要把赌金先给结算了，毕竟ytty今天人品大爆发，赢了hh两局。
所以问题来了，这个赌金应该怎么分配呢？
存在的问题：规定的先赢3局的目标还没有完成，所以不能给yty全部的赌金；而且也不能平分，因为hh比yty少赢1局，yty会不爽的。
解答：
这就要跟概率牵扯起来了。对于下一局，yty和hh赢的概率各是50%，如果是yty赢，那么整场赌博游戏就是yty赢了；如果是hh赢，2：2就打平了，那么双方就需要额外进行决胜局。对于决胜局，yty赢得几率是25%（50%*50%），整场赌博游戏yty赢的几率就是前面的50%+现在的25%，共75%；hh赢的几率是25%。因此赌金应该yty：hh=3:1的比值分配。

事件发生的概率

我们先约定，当我们在一个特定的环境下，A、B等代表可能发生的所有单个事件，S代表所有可能发生的单个事件的集合。所以有A∈S，B∈S。
如果有一个集合是C，满足C∩S=∅，我们就说C是“不可能事件”，如果有一个集合D，满足D=S，就说D是必然事件。因为不管S中的事件发生多少次，C都不可能发生，D都一定发生。（是不是有点绕口，一定要啃完）

和事件和积事件

事件A∪B称为事件A和事件B的和事件（A∪B可以理解为A or B，即A和B任意发生一个），如果A和B至少任意发生一个，我们就说事件A∪B发生。A∪B有时候也记作A+B。
事件A∩B称为事件A和事件B的积事件（A∩B可以理解成A and B，即A和B同时发生），如果A和B同时发生，我们就说A∩B发生。A∩B有时候也记作A*B。
当有多个事件的时候我们可以用 ⋃nk=1Ak 和 ⋂nk=1Ak 。

互斥和互补

如果A∩B=∅，称事件A和事件B互斥，指A和B不能同时发生。
如果A∪B=S，且A∩B=∅，称事件A和事件B互为对立事件（补集）。对立事件的性质是，对于每一次试验，都是事件A和事件B一定有且只有一个发生。

频率和概率

频率：在相同的条件下，进行了n次试验，在n次试验中，事件A发生了 NA/n 次，那么 NA/n 称为事件A发生的频率（n是频数）。
我们可以发现，当n=∞时，对于相同事件，频率无限接近概率。

概率的性质

我们设事件A发生的概率是P（A），那么有：

1. 非负性：对于任何事件A，都有 0≤P（A）≤1 ；
2. 规范性：对于每个必然事件A， P（A）=1 ；每个不可能事件A， P（A）=0 ；
3. 互斥性：对于任意两个事件A和B， P（A∪B）=P（A）+P（B）−P（A∩B） ；
4. 互斥事件的可加性：如果事件A和B是互斥的，那么 P（A∪B）=P（A）+P（B）
5. 对立事件的概率之和=1；
6. 独立事件的可乘性：如果A和B之间是相互不干扰的，我们就说A和B是相互独立的事件，那么就有 P（A∩B）=P（A）∗P（B） ；
7. 伯努利大数定理：如果在一次实验中，某事件发生的概率是p，不发生的概率是q，则在n次试验中至少发生m次的概率等于 （p+q）n 的 展开式 中从 pn 到包括 pmqn−m 为止的各项之和。 如果在一次实验中，某事件发生的概率为p，那么在n次独立重复的试验中这个事件恰好发生k次（ 0≤k≤n ）的概率是 Pn(k)=Cnk∗pk∗(1−p)n−k 。

例题

yty找文件

yty有一张书桌，有8个抽屉，分别用数字1~8编号。每次拿到一个文件后，他都会把这份文件随机地放在某一个抽屉中。但是，可怜的yty非常粗心，有 15 的概率会忘了把这个文件放进抽屉，最终因为没有放进抽屉而把文件弄丢。现在，yty要找一个文件，他按照编号顺序依次打开每一个抽屉，直到找到这份文件为止，或者最终发现文件已经丢失。请回答下列问题：

1. 如果yty打开了第一个抽屉，但是没有发现他要的文件，请问这份文件在其余7个抽屉的概率是多少？
2. 如果yty打开了前4个抽屉，里面没有发现他要的文件，请问这份文件在其余4个抽屉里的概率是多少？
3. 如果yty打开了前7个抽屉，里面没有他要的文件，请问这份文件在最后一个抽屉里的概率是多少？

解析：
答案是 79 、 23 和 13 ，如你所见，概率是越来越小的。我们应该怎么计算呢？
因为上文提到过了，yty弄丢文件的概率是 15 也就是说，10份文件中，有2份弄丢，其余8份放进了yty有的8个抽屉。我们可以这样想：假设又多了两个编号为9和10的抽屉，并且这两个抽屉是“无底洞”，扔进去的文件都找不回来了。那么就好办了，设yty已经翻过了n个抽屉，那么我们就是求文件在前（8-n）个抽屉的概率，显然剩余（10-n）个抽屉，所以我们的方法就是： 8−n10−n 把不同的n值带进去就可以求出来了。

古典概率

古典概率也叫事前概率，也就是在事情发生之前我们就可以推算出来任何事件发生的概率。概率用的最早就是一些概率游戏和赌博中。
古典概率有几个特点：

1. 样本容量有限；
2. 事件可能性相同；
3. 事件互斥；

就像丢硬币，只有两种可能，而且每种可能都是50% ，丢了正面就不会同时丢反面（除非你立起来，不过你也可以尝试下几次之后能立起来），这些具有这样的特点的随机试验我们称之为古典概型或者等可能概型。计算古典概型的方法称为概率的古典定义或者古典概率。
在计算古典概率的时候，如果在全部可能出现的基本事件范围内构成事件A的基本事件有 an 个，不构成事件A的基本事件有 bn 个，且那么出现事件A的概率是 P（A）=a/（a+b） 。

例题

yty买圆珠笔

yty受厉总委托，去商店买一些子圆珠笔。yty到商店后，发现商店还剩下40支圆珠笔，在这40支圆珠笔中有30支是黑色的，10支是红色的。yty需要买4支圆珠笔，请问yty随机买4支圆珠笔，至少买到一支红笔的概率？
方法一——分解问题
设从40支笔中任意取出4支，恰好有1支或者2支或者3支或者4支红笔的事件记为A、B、C、D。我们有：
P（A）=C110∗C330/C440=40600/91390
P（B）=C210∗C230/C440=19575/91390
P（C）=C310∗C130/C440=3600/91390
P（D）=C410∗C030/C440=210/91390
根据题意，事件A、B、C、D两两互质，所以 P（A∪B∪C∪D）=P（A）+P（B）+P（C）+P（D）=63985/91390≈0.7 ；
方法二——对立
我们也可以从对立事件的概率来分析，设从40支笔中取4支全是黑色的事件为A，则有 P（A）=C430/C440=27405/91390≈0.3 。所以，对立事件的概率是0.7。

数学期望

数学期望可以理解为某件事情大量发生之后的平均结果（这个事件的概率会受一些因素的干扰），可以这样分辨：概率针对几率，而期望是针对的最终结果。我们举个例子：对于一个骰子，每个面的概率都是 16 ，但是你大量投骰子之后的数学期望值是： 1∗16+2∗16+3∗16+4∗16+5∗16+6∗16=3.5
我们举个赌博的例子吧：

yty杀回赌场

yty在上一次赌博游戏之后感觉很不服，”为什么？？我赢的场数比hh多，hh本应该输的，怎么还能拿25%的赌金呢？？？“于是乎就又去找hh赌博，并规定了以下规则：

1. 关掉手机（避免上次的情况）；
2. 赌博道具：14张扑克牌，有一张是A；
3. 游戏规则：yty进行坐庄，hh在14张牌里面抽取任意一张牌，如果hh抽到了A，那么yty给hh10块钱；如果hh没有抽到A，那么hh给yty1块钱；

在这场游戏中，看起来好像是有利于hh的，因为hh抽取一张牌就有两种情况：1种是抽到A，一种情况是没有抽到A。但是大错特错，因为抽到A和不抽到A的概率是不相同的。从hh的角度看，抽取到A的概率是 114 ，收益是10；没有抽取到的概率， 1314 ，收益是-1；所以我们可以算出数学期望： 114∗10+1314∗（−1）=−314<0 所以hh是绝对亏的。

计算公式

所以我们在算数学期望值的时候不能简单地使用古典概率的计算方法，不能只考虑样本容量，还得考虑样本中每个事件出现的概率。
假设我们规定： x1,x2,x3 ……是随机输出值（在投骰子中，就是1 、2 、3 、4 、5 、6），这些随机输出值对应的概率就是 p1,p2,p3 ……（当然 ∑ipi=1 ），所以数学期望值的公式： E（X）=∑ipixi 。

拓展公式

1. 期望的“线性”性质。对于任何随机变量X和Y以及常量a和b，有： E（aX+bY）=aE（X）+bE（Y） 。
2. 全概率公式。假设{ Bn|n=1,2,3,… }是一个概率空间的有限或者可数无限的分割，且每个集合 Bn 是一个可测集合，则对任意事件A有全概率公式： P（A）=∑nP（A|Bn）P（Bn） 。其中：P（A|B）是B发生后A的条件概率。
3. 全期望公式。 pij=P(X=xi,Y=yj)(i,j=1,2,…) ，当 X=xi 时，随机变量Y的条件期望以 E（Y|X=xi） 表示。则全期望公式：
   
   E（E（Y|X））=∑iP（X=xi）E（Y|X=xi）=∑ipi∑kykpikpi=∑i∑kpiykpikpi=∑i∑kykpik=E（Y）
   
   所以： E（Y）=E（E（Y|X））=∑iP（X=xi）E（Y|X=xi）
   对于全期望我们来举个例子吧。

yty的工作

yty跟hh赌博了三天三夜之后，真的赌地身无分文。无奈下，只能去搬砖。如果yty一个人搬砖，平均需要4小时，而hh有0.4的概率来帮yty搬砖，两个人一起搬砖平均只需要3小时。若用X表示完成搬砖的人数，而Y表示完成搬砖的期望时间（单位小时），由于这项搬砖的工作要么由yty单独完成，要么由yty和hh共同完成，那么搬砖的工作完成的期望时间是 E（Y）=P（X=1）E（Y|X=1）+P（X=2）E（Y|X=2）=（1−0.4）∗4−0.4∗3=3.6 。

用递推解决期望问题

对于期望问题，递推是一种快速有效的解决方法。我们不需要将所有可能的情况都枚举出来，而是根据已经求出的期望推出其他状态的期望，也可以根据一些特点和结果相同的情况，求出其概率。
对于一些比较难找到递推关系的数学期望问题，可以利用期望的定义式： E（X）=∑ipixi ，根据实际情况以概率或者方案数（也就是概率*总方案数）作为一种状态，而下标直接或间接对应了这个概率下的变量值（有没有哈希的味道），将问题变成比较一般的统计方案数问题或者利用全概率公式计算概率的递推问题。对于另外一些带有决策的期望问题，可以使用DP解决，这类题由于要满足最优子结构，一般都用期望来表示状态，而期望正或负表现了这单个状态的优或劣。对于递推和动态规划都无法有效结局的模型，由于迭代的效率低，而且迭代的致命缺点是无法得到精确解，可以建立线性方程组并利用高斯消元的方法来解决。（高斯消元待博客）

例题——yty的百事世界杯之旅

题目

题目描述
“……在2002年6月之前购买的百事任何饮料的瓶盖上都会有一个百事球星的名字。只要凑齐所有百事球星的名字，就可参加百事世界杯之旅的抽奖活动，获得球星背包，随声听，更可赴日韩观看世界杯。还不赶快行动！”
yty关上电视，心想：假设有n个不同的球星名字，每个名字出现的概率相同，平均需要买几瓶饮料才能凑齐所有的名字呢？
yty心动了。开始了一波编程计算：

输入输出格式
输入格式：
整数n（2≤n≤33），表示不同球星名字的个数。
输出格式：
输出凑齐所有的名字平均需要买的饮料瓶数。如果是一个整数，则直接输出，否则应该直接按照分数格式输出，例如五又二十分之三应该输出为（复制到记事本）：
3 5– 20 第一行是分数部分的分子，第二行首先是整数部分，然后是由减号组成的分数线，第三行是分母。减号的个数应等于分母的为数。分子和分母的首位都与第一个减号对齐。
分数必须是不可约的。

输入输出样例
输入样例#1：
2
输出样例#1：
3

分析

这道题目用期望的语言来说就是：“我们期望买多少饮料能够搞到所有的奖品”。

这道题目我们可以采用递推求数学期望的方法。我们设 f(n,k) 是一共有n个球星，而且现在还剩下k个球星没有收集到，还需要购买饮料的期望次数。所以我们最后要求取的答案是 f(n,n) 。

假设我们现在推到了 f(n,k) ，我们再买一瓶饮料，有两种可能性，一种是：我们买到了我们没有拥有的球员，那么剩下的子问题就是 f(n,k−1) ；如果买到了我们拥有的球员，那么剩下的子问题就是 f(n,k) 。然而我们任意买一个瓶盖，有 kn 的可能性买到我们没有的，有 n−kn 的可能性买到我们已经有的。所以这道题目的递推是就是：

f(n,k)=(n−k)f(n,k)n+kf(n,k−1)n+1

然后呢，经过移项，会有

f(n,k)=f(n,k−1)+nk

这就是一个递推式了。

代码

#include
using namespace std;
int n;
long long p,q=1,r;
inline int cc(long long x)//cc函数用来统计数x的位数
{
    int p=0;//p用来记录最后的答案
    while(x>0)
    {
        x/=10;
        p++;
    }//非常小儿科的求位数
    return p;
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        p=p*i+q*n;
        q*=i;
        //递推
        r=__gcd(p,q);
        /*__gcd函数。这是一个库函数，是用来求
        两个数的最大公约数的。但是由于功能过于
        强大，ccf已经规定了：所有下划线开头的
        库函数都不能在oi中使用。*/
        p/=r;
        q/=r;//分数的约分。
    }//这部分是用来求最后结果的，p放分子，q放分母
    r=p/q;
    p%=q;
    /*把这个分数化成带分数的形式，r存放整数部分，
    p和q放分子和分母。*/
    if(p==0)
    {
        printf("%lld\n",r);
        return 0;
    }//如果分子为0，就说明答案是整数，直接输出整数部分
    for(int i=1;i<=cc(r);i++)
    printf(" ");
    //为了对齐补充的空格。

    if(r>0)
    printf("%lld",r);
    //这里要慎重：如果p==0，则不用输出

    for(int i=1;i<=cc(q);i++)
    printf("-");
    //分数线长度是分母的长度
    printf("\n");

    for(int i=1;i<=cc(r);i++)
    //为了对齐补充的空格。
    printf("%lld\n",q);
    return 0;
}

概率 习题

例题一

题目背景
从前有一个聪明的小魔女帕琪，兴趣是狩猎吸血鬼。
帕琪能熟练使用七种属性（金、木、水、火、土、日、月）的魔法，除了能使用这么多种属性魔法外，她还能将两种以上属性组合，从而唱出强力的魔法。比如说为了加强攻击力而将火和木组合，为了掩盖弱点而将火和土组合等等，变化非常丰富。

题目描述
现在帕琪与强大的夜之女王，吸血鬼蕾咪相遇了，夜之女王蕾咪具有非常强大的生命力，普通的魔法难以造成效果，只有终极魔法：帕琪七重奏才能对蕾咪造成伤害。帕琪七重奏的触发条件是：连续释放的7个魔法中，如果魔法的属性各不相同，就能触发一次帕琪七重奏。
现在帕琪有7种属性的能量晶体，分别为a1,a2,a3,a4,a5,a6,a7(均为自然数)，每次释放魔法时，会随机消耗一个现有的能量晶体，然后释放一个对应属性的魔法。
现在帕琪想知道，她释放出帕琪七重奏的期望次数是多少，可是她并不会算，于是找到了学OI的你

输入输出格式
输入格式：
一行7个数字，a1,a2,a3,a4,a5,a6,a7
输出格式：
一个四舍五入保留3位的浮点数

输入输出样例
输入样例#1：
1 1 1 1 1 1 1
输出样例#1：
1.000

分析

这道题目的代码很短，但是可以让你对概率的基本概念有较深刻和较准确的理解。题目的基本意思就是说要从所有的魔法晶体中找出一个七元素集合：这个集合包含了所有的元素。然后再把所有的元素进行全排列。

代码

#include
using namespace std;
int a[10]; 
int main()
{
    int sum=0;
    for(int i=1;i<=7;i++)
    {
        scanf("%d",&a[i]);
        sum+=a[i];
    }//读入+求和
    printf("%.3lf",1.0*5040*a[1]/sum*a[2]/(sum-1)
    *a[3]/(sum-2)*a[4]/(sum-3)*a[5]/(sum-4)
    -*a[6]/(sum-5)*a[7]);
/*
首先要保留了三位小数的实型变量，所以是.3lf；但是后面的算
式里面都是整形变量参加的运算，所以要*1.0强制转化成实型。

然后我们知道要任意这样排列的总数，所以我们可以先找到一种组
合，然后进行全排列，就得到了排列的总数。上文中5040是7的阶
乘，也就是进行全排列的过程。

然后我们来解释下后面的算式的意思：
我们完成一次组合的要进行7次施法，第一次随机施法用第一种魔
法球的概率是a[1]/sum，第二次由于第一次用掉了一个魔法球，
所以在剩余的魔法球中找到一个第二种魔法球的概率是
a[2]/（sum-1）……以此类推吧。然后最后是因为还剩下
sum-6个魔法球，这些魔法球还可以生成上述的组合，
所以总数要*（sum-6）
*/
    return 0;
}

例题二

题目背景
四川NOI2008省选

题目描述
你有 n 个整数Ai和n 个整数Bi。你需要把它们配对，即每个Ai恰好对应一个Bp[i]。要求所有配对的整数差的绝对值之和尽量小，但不允许两个相同的数配对。例如A={5,6,8}，B={5,7,8}，则最优配对方案是5ó8, 6ó5, 8ó7，配对整数的差的绝对值分别为2, 2, 1，和为5。注意，5ó5，6ó7，8ó8是不允许的，因为相同的数不许配对。

输入输出格式
输入格式：
第一行为一个正整数n，接下来是n 行，每行两个整数Ai和Bi，保证所有
Ai各不相同，Bi也各不相同。
输出格式：
输出一个整数，即配对整数的差的绝对值之和的最小值。如果无法配对，输
出-1。

输入输出样例
输入样例#1：
3
3 65
45 10
60 25
输出样例#1：
32
输入样例#2：
3
5 5
6 7
8 8
输出样例#2：
5

说明
30%的数据满足：n <= 10^4
100%的数据满足：1 <= n <= 10^5，Ai和Bi均为1到10^6之间的整数。

分析

先来一发吐槽：网上很多的题解都是这样一句话：“这尼玛太难了，我不会”；“至于证明的话，请用好搜索引擎”“至于证明，我也不会”…………所以这里分析需要好好琢磨一下，真的很难懂
这里有个基本的结论：对a数组和b数组排序好之后，对于任意一个数a[i]，在b数组中只有5个数和它可以匹配：b[i],b[i-1],b[i-2],b[i+1],b[i+2]。
我们可以画图证明一下，

这里的情况就是跟超过了2个数的位置进行了匹配，我们可以发现一定存在一种结构可以这样优化成以下结构：

但是这种情况为什么不能直接被继续分解的结构代替呢，因为数据允许相等。。。

代码

#include
#define maxn 100050
#define INF 100000000
using namespace std;
long long n,a[maxn],b[maxn],f[maxn];
//f数组用来代表前i个数匹配的匹配最小值
long long c(long long x,long long y)
{
    return a[x] == b[y] ? INF : abs(a[x] - b[y]);
}
/*这是计算匹配值的一个函数，也就是两个数的差的绝对值,
但是如果这两个数相等，我们就认为这两个数的匹配值无限大。
那么我们在接下来选取最小匹配值，就不会把这一组匹配给选进去了*/
int main()
{
    scanf("%lld",&n);
    for(int i=1;i<=n;i++)
    scanf("%lld%lld",&a[i],&b[i]);
    //读入两个数组
    sort(a+1,a+1+n);
    sort(b+1,b+1+n);
    //分别排序
    memset(f,0,sizeof(f));
    f[1]=c(1,1);
    //前1个数匹配最小值只能是a[1]和b[1]匹配
    f[2]=min(f[1]+c(2,2),c(1,2)+c(2,1));
    /*前两个数的匹配最小值只能是a[1]和b[1]，a[2]和b[2]；
    或者a[1]和b[2]，a[2]和b[1]匹配。*/
    for(int i=3;i<=n;i++)//开始dp
    {
        f[i]=f[i-1]+c(i,i);//默认是这样匹配（先给一个初值，再不断被更新）
        f[i] = min(f[i],f[i-2]+c(i-1,i)+c(i,i-1));
        f[i] = min(f[i],f[i-3]+c(i-2,i)+c(i,i-2)+c(i-1,i-1));
        f[i] = min(f[i],f[i-3]+c(i-2,i)+c(i-1,i-2)+c(i,i-1));
        f[i] = min(f[i],f[i-3]+c(i-2,i-1)+c(i-1,i)+c(i,i-2));
        //四种交叉匹配的方案，大家可以在草稿纸上画画线条模拟匹配一下子
    }
    printf("%lld",f[n]>=INF?-1:f[n]);
    //如果f[n]>=INF就说明不能匹配，就输出-1。否则就是正解了。
    return 0;
}

例题三

题目描述

对于刚上大学的牛牛来说，他面临的第一个问题是如何根据实际情况申请合适的课程。

在可以选择的课程中，有 2n 节课程安排在 n 个时间段上。在第 i（1≤i≤n） 个时间段上，两节内容相同的课程同时在不同的地点进行，其中，牛牛预先被安排在教室 ci 上课，而另一节课程在教室 di 进行。
在不提交任何申请的情况下，学生们需要按时间段的顺序依次完成所有的 n 节安排好的课程。如果学生想更换第 i 节课程的教室，则需要提出申请。若申请通过，学生就可以在第 i 个时间段去教室 di 上课，否则仍然在教室 ci 上课。
由于更换教室的需求太多，申请不一定能获得通过。通过计算，牛牛发现申请更换第 i 节课程的教室时，申请被通过的概率是一个已知的实数 ki ，并且对于不同课程的申请，被通过的概率是互相独立的。
学校规定，所有的申请只能在学期开始前一次性提交，并且每个人只能选择至多 m 节课程进行申请。这意味着牛牛必须一次性决定是否申请更换每节课的教室，而不能根据某些课程的申请结果来决定其他课程是否申请；牛牛可以申请自己最希望更换教室的 m 门课程，也可以不用完这 m 个申请的机会，甚至可以一门课程都不申请。
因为不同的课程可能会被安排在不同的教室进行，所以牛牛需要利用课间时间从一间教室赶到另一间教室。
牛牛所在的大学有 v 个教室，有 e 条道路。每条道路连接两间教室，并且是可以双向通行的。由于道路的长度和拥堵程度不同，通过不同的道路耗费的体力可能会有所不同。 当第 i（1≤i≤n−1） 节课结束后，牛牛就会从这节课的教室出发，选择一条耗费体力最少的路径前往下一节课的教室。
现在牛牛想知道，申请哪几门课程可以使他因在教室间移动耗费的体力值的总和的期望值最小，请你帮他求出这个最小值。

输入输出格式
输入格式：
第一行四个整数 n,m,v,e 。 n 表示这个学期内的时间段的数量； m 表示牛牛最多可以申请更换多少节课程的教室； v 表示牛牛学校里教室的数量； e表示牛牛的学校里道路的数量。第二行 n 个正整数，第 i（1 \leq i \leq n） 个正整数表示 c_i ，即第 i 个时间段牛牛被安排上课的教室；保证 1 \le c_i \le v 第三行 n 个正整数，第 i（1 \leq i \leq n） 个正整数表示 d_i ，即第 i 个时间段另一间上同样课程的教室；保证 1 \le d_i \le v 第四行 n 个实数，第 i（1 \leq i \leq n） 个实数表示 k_i ，即牛牛申请在第i个时间段更换教室获得通过的概率。保证 0 \le k_i \le 1 接下来 e 行，每行三个正整数 a_j, b_j, w_j ，表示有一条双向道路连接教室 a_j, b_j ，通过这条道路需要耗费的体力值是 w_j ；保证 1 \le a_j, b_j \le v ​, 1 \le w_j \le 100 保证 1 \leq n \leq 2000，0 \leq m \leq 2000，1 \leq v \leq 300，0 \leq e \leq 90000 。保证通过学校里的道路，从任何一间教室出发，都能到达其他所有的教室。保证输入的实数最多包含3位小数。输出格式：输出一行，包含一个实数，四舍五入精确到小数点后恰好22位，表示答案。你的输出必须和标准输出完全一样才算正确。测试数据保证四舍五入后的答案和准确答案的差的绝对值不大于 4 \times 10^{-3}$。 （如果你不知道什么是浮点误差，这段话可以理解为：对于大多数的算法，你可以正常地使用浮点数类型而不用对它进行特殊的处理）

输入输出样例
输入样例#1：
3 2 3 3
2 1 2
1 2 1
0.8 0.2 0.5
1 2 5
1 3 3
2 3 1
输出样例#1：
2.80
说明
【样例1说明】
所有可行的申请方案和期望收益如下表:

【提示】
1.道路中可能会有多条双向道路连接相同的两间教室。 也有可能有道路两端连接的是同一间教室。
2.请注意区分n,m,v,e的意义, n不是教室的数量, m不是道路的数量。

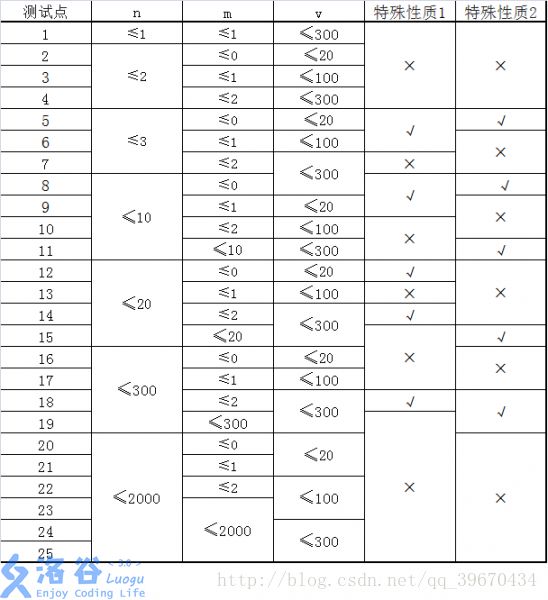
特殊性质1:图上任意两点 ai , bi , ai≠bi 间,存在一条耗费体力最少的路径只包含一条道路。
特殊性质2:对于所有的 1≤i≤n , ki=1 .

分析

这道题目是一个图的期望DP。我们要算的期望是到每一个时间点为止的路径最大值。
思路是：我们先用floyd进行预处理（因为v的数据很小，可以使用邻接矩阵），然后就开始期望dp。
我们的状态用一个三维数组存储：f[i][j][k]表示到了第 i 个时间段，选了j个教室要申请进行换教室，k表示当前的教室申不申请。我们从i推到 i+1。这里要进行分类讨论，如果要推到f[i][j][0]的话，那么第i+1个时间段肯定是在c[i+1]教室（因为不进行申请，失败的概率可以理解为百分之一百），但是来这个教室之前，我们可以讨论上一个时间段的情况：如果上一个时间段没有进行申请，那么上一个时间段肯定在c[i]，那么期望是a[c[i]][c[i+1]]*1(100%的概率)；如果上个时间段进行了申请，那么就存在两个情况，申请成功和申请不成功，所以上个时间段可能在c[i]或者d[i]。概率是1-k[i]和k[i]，再进行期望计算：

f[i+1][j][0]=min(f[i][j][0]+a[c[i]][c[i+1]],f[i][j][1]+(1−k[i])×a[c[i]][c[i+1]]+k[i]×a[d[i]][c[i+1]])

如果这个时间段进行申请，那么差不多地，我们还进行讨论：
若j!=m（代表还没有到申请数量上限）：

f[i+1][j+1][1]=min(f[i][j][0]+a[c[i]][d[i+1]]×k[i+1]+a[c[i]][c[i+1]]×(1−k[i+1]),f[i][j][1]+a[c[i]][c[i+1]]×(1−k[i])×(1−k[i+1])+a[d[i]][c[i+1]]×k[i]×(1−k[i+1])+a[c[i]][d[i+1]]×(1−k[i])×k[i+1]+a[d[i]][d[i+1]]×k[i]×k[i+1]);

否则就不能申请了。。。

代码

#include
#define maxn 2001
#define maxe 90001
#define maxv 301//宏定义，我被带掉了
#define INF 100000000
using namespace std;
inline int read()
{
    int num=0;
    char c=getchar();
    for(;c>'9'||c<'0';c=getchar());
    for(;c>='0'&&c<='9';num=num*10+c-48,c=getchar());
    return num;
}
int n,m,v,e,c[maxn],d[maxn];
double k[maxn];
double f[maxn][maxn][2];
int a[maxv][maxv];//a数组代表i和j之间的最短路（用弗洛伊德可以完成） 
void init()
{
    n=read();
    m=read();
    v=read();
    e=read();
    memset(a,10,sizeof(a));
    for(int i=1;i<=n;i++)
    c[i]=read();
    for(int i=1;i<=n;i++)
    d[i]=read();
    for(int i=1;i<=n;i++)
    cin>>k[i];
    for(int i=1;i<=e;i++)
    {
        int x,y,z;
        x=read();
        y=read();
        z=read();
        a[x][y]=a[y][x]=min(z,a[x][y]);
    }
}//读入 

void floyd()
{
    for(int i=1;i<=v;i++)
    a[i][i]=0;//坑1：防止自环
    for(int k=1;k<=v;k++)
    for(int i=1;i<=v;i++)
    for(int j=1;j<=v;j++)
    a[i][j]=min(a[i][j],a[i][k]+a[k][j]);
    for(int i=1;i<=v;i++)
    a[0][i]=0;//坑2：增加超级源点防止溢出导致不可预测的错误
}//弗洛伊德做最短路 

int main()
{
    init();//读入 
    floyd();//弗洛伊德 
    for(int i=0;ifor(int j=0;jfor(int k=0;k<=1;k++)
    f[i][j][k]=INF;//赋初值

    f[0][0][0]=0;//dp起点
    for(int i=0;i<=n-1;i++)//进行dp递推
    {
        for(int j=0;j<=m;j++)
        {
            f[i+1][j][0]=min(f[i][j][0]+a[c[i]][c[i+1]],f[i][j][1]+(1-k[i])*a[c[i]][c[i+1]]+k[i]*a[d[i]][c[i+1]]);
            if(j!=m)f[i+1][j+1][1]=min(f[i][j][0]+a[c[i]][d[i+1]]*k[i+1]+a[c[i]][c[i+1]]*(1-k[i+1]),
            f[i][j][1]+a[c[i]][c[i+1]]*(1-k[i])*(1-k[i+1])+a[d[i]][c[i+1]]*k[i]*(1-k[i+1])+a[c[i]][d[i+1]]*(1-k[i])*k[i+1]+a[d[i]][d[i+1]]*k[i]*k[i+1]);
        }
    }
    double ans=INF;
    for(int j=0;j<=m;j++)
    ans=min(ans,min(f[n][j][0],f[n][j][1]));
    printf("%.2lf",ans);//坑3：小数点
    return 0;
}