LeetCode_数组_简单题
目录
- 26.删除排序数组中的重复项
- 27.移除元素
- 53.最大子序和
- 66.加一
- 88.合并两个有序数组
- 118.杨辉三角形
- 119.杨辉三角形II
- 717.1比特与2比特字符
- 989.数组形式的整数加法
- 561.数组拆分I
- 1491.去掉最低工资和最高工资后的工资平均值
- 121.买卖股票的最佳时机
- 122.买卖股票的最佳时机II
- 1018.可被5整除的二进制前缀(没懂)
- 1502.判断能否形成等差数列
- 605.种花问题
- 1351.统计有序矩阵中的负数
26.删除排序数组中的重复项
int removeDuplicates(int* nums, int numsSize){
if(numsSize==0){
return 0;
}
int i = 0,j;
for(j=1; j<numsSize; j++){
if(nums[j]!=nums[i]){
i++;
nums[i] = nums[j];
}
}
return i+1;
}
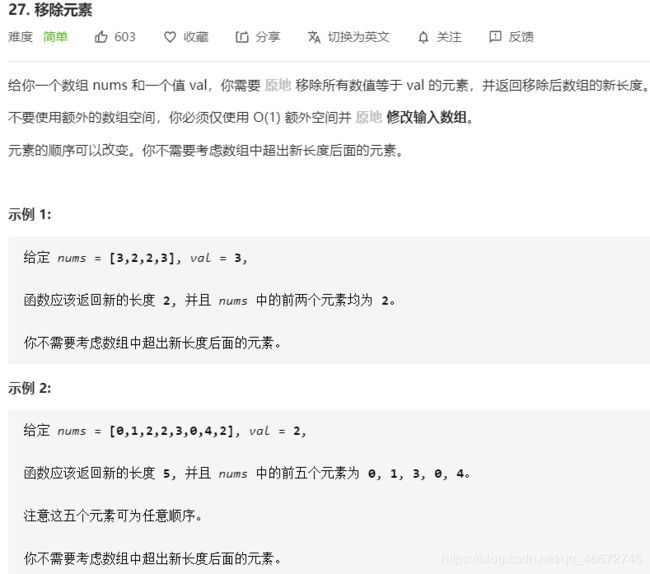
27.移除元素
int removeElement(int* nums, int numsSize, int val){
int i = 0,j;
for(j=0; j<numsSize; j++){
if(nums[j]!=val){
nums[i]=nums[j]; //nums[i]为新数组
i++;
}
}
return i;
}
53.最大子序和
int maxSubArray(int* nums, int numsSize){
int subsum = 0, maxsum = -2147483648;
for(int i = 0; i < numsSize; i ++)
{
subsum += nums[i];
if(subsum > maxsum)
{
maxsum = subsum;
}
if(subsum < 0) subsum = 0;
}
return maxsum;
}
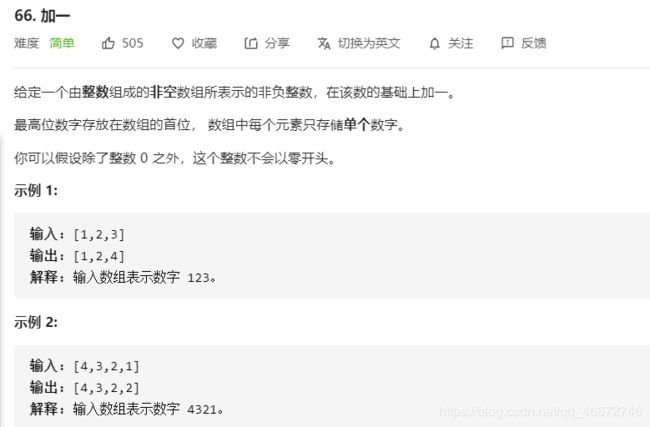
66.加一
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* plusOne(int* digits, int digitsSize, int* returnSize){
if (digits == NULL && digitsSize == 0){ //传参检查
*returnSize = 0;
return NULL;
}
int flag = 0; //进位标志
int i = digitsSize - 1; //数组下标
int* res = (int*)malloc((digitsSize+1) * sizeof(int));
//申请多一位空间(最高位产生进位)
digits[i] = digits[i] + 1;//最低位 + 1
//特别注意这里改变了源数据,这点不太好,值得改进
for (; i >= 0; --i){
res[i] = digits[i] + flag;
if (res[i] >= 10){//判断有无进位
res[i] = res[i]%10;
flag = 1;
}
else{
flag = 0;
}
}
*returnSize = digitsSize + flag;
if (flag != 0){ //最高位产生了进位
int tmp;
int mid = flag; //进位数 赋给 数组第一位(新的最高位)
for (i = 0; i <= digitsSize; ++i){
tmp = res[i]; //保存当前值
res[i] = mid;
mid = tmp; //移动至下一个位置
}
}
return res;
}
88.合并两个有序数组
//由后向前排
void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n){
int tag1=m-1; //nums1最后一个元素数组下标
int tag2=n-1; //nums2最后一个元素数组下标
int end=m+n-1; //目标nums1处理下标
while(end>-1){
if(tag1<0){ //处理边界问题,防止nums[tag]数组越界
nums1[end]=nums2[tag2];
tag2--;
}
else if(tag2<0){
nums1[end]=nums1[tag1];
tag1--;
}
else if(nums1[tag1]>nums2[tag2]){
nums1[end]=nums1[tag1];
tag1--;
}
else{
nums1[end]=nums2[tag2];
tag2--;
}
end--;
}
}
题解_Java
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
System.arraycopy(nums2, 0, nums1, m, n); //将俩个数组合并
Arrays.sort(nums1); //对合并后的新数组排序 缺点:没考虑俩个旧数组已经是有序的
}
}
118.杨辉三角形
/**
* Return an array of arrays of size *returnSize.
* The sizes of the arrays are returned as *returnColumnSizes array.
* Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
*/
int** generate(int numRows, int* returnSize, int** returnColumnSizes){
*returnSize = numRows;
*returnColumnSizes = (int*)malloc(4*numRows);
int i,j;
int **ret = (int**)malloc(sizeof(int*)*numRows); //声明
for(i=0; i<numRows; i++){
(*returnColumnSizes)[i] = i+1; //初始化
ret[i] = (int*)malloc(i*4+4);
ret[i][0] = 1;
ret[i][i] = 1;
}
for(i=2; i<numRows; i++){
for(j=1; j<i; j++){
ret[i][j] = ret[i-1][j-1] + ret[i-1][j]; //计算
}
}
return ret;
}
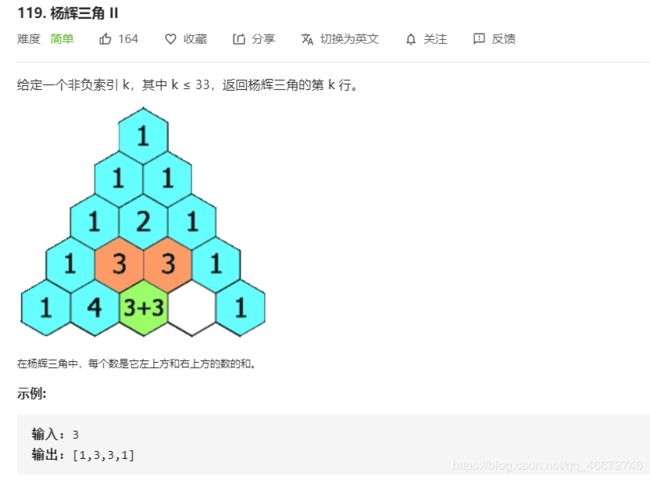
119.杨辉三角形II
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
//申请一行的空间,从后往前处理就不需要考虑数组元素被处理时被覆盖的问题。
int* getRow(int rowIndex, int* returnSize){
* returnSize = rowIndex + 1; //第k行有k个元素
int* array = (int *)malloc(sizeof(int) * (rowIndex+1));
for(int i=0; i<rowIndex+1; i++){
array[i]=1; //行末尾为1
for(int j=i-1; j>0; j--){ //每一行的更新过程
array[j] = array[j] + array[j-1];
}
array[0] = 1;
}
return array;
}
717.1比特与2比特字符

方法一:线性扫描
我们可以对 \mathrm{bits}bits 数组从左到右扫描来判断最后一位是否为一比特字符。当扫描到第 ii 位时,如果 \mathrm{bits}[i]=1bits[i]=1,那么说明这是一个两比特字符,将 ii 的值增加 2。如果 \mathrm{bits}[i]=0bits[i]=0,那么说明这是一个一比特字符,将 ii 的值增加 1。
如果 ii 最终落在了 \mathrm{bits}.\mathrm{length}-1bits.length−1 的位置,那么说明最后一位一定是一比特字符。
bool isOneBitCharacter(int* bits, int bitsSize){
int i = 0;
while(i<bitsSize-1){
i += bits[i] + 1;
}
return i == bitsSize - 1;
}
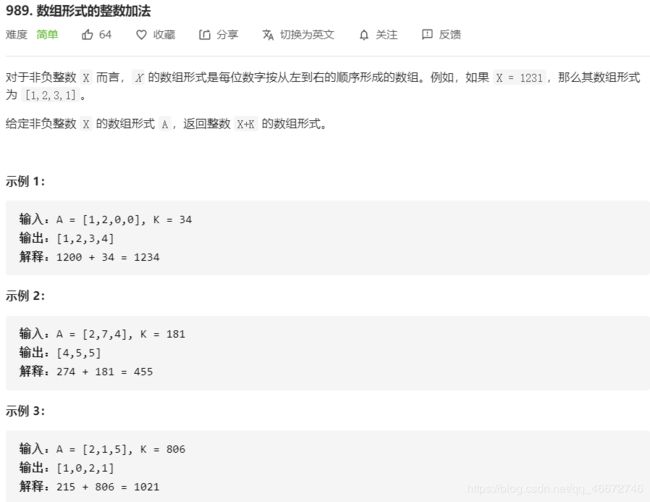
989.数组形式的整数加法
让我们逐位将数字加在一起。举一个例子,如果要计算 123123 与 912912 的和。我们顺次计算 3+23+2、2+12+1、1+91+9。任何时候,当加法的结果大于等于 1010,我们要将进位的 11 加入下一位的计算中去,所以最终结果等于 10351035。
算法
我们可以对以上的想法做一个小变化,让它实现起来更容易 —— 我们将整个加数加入数组表示的数的最低位。
继续之前的例子 123+912123+912,我们把它表示成 [1, 2, 3+912][1,2,3+912]。然后,我们计算 3+912 = 9153+912=915。55 留在当前这一位,将 910/10=91 以进位的形式加入下一位。
然后,我们再重复这个过程,计算 [1, 2+91, 5][1,2+91,5]。我们得到 9393,33 留在当前位,将0/10=9 以进位的形式加入下一位。继而又得到 [1+9, 3, 5][1+9,3,5],重复这个过程之后,最终得到结果 [1, 0, 3, 5][1,0,3,5]。
class Solution {
public List<Integer> addToArrayForm(int[] A, int K) {
int N = A.length;
int cur = K;
List<Integer> ans = new ArrayList();
int i = N;
while (--i >= 0 || cur > 0) {
if (i >= 0)
cur += A[i];
ans.add(cur % 10);
cur /= 10;
}
Collections.reverse(ans);
return ans;
}
}
561.数组拆分I
public class Solution {
public int arrayPairSum(int[] nums) {
Arrays.sort(nums);
int sum = 0;
for (int i = 0; i < nums.length; i += 2) {
sum += nums[i];
}
return sum;
}
}
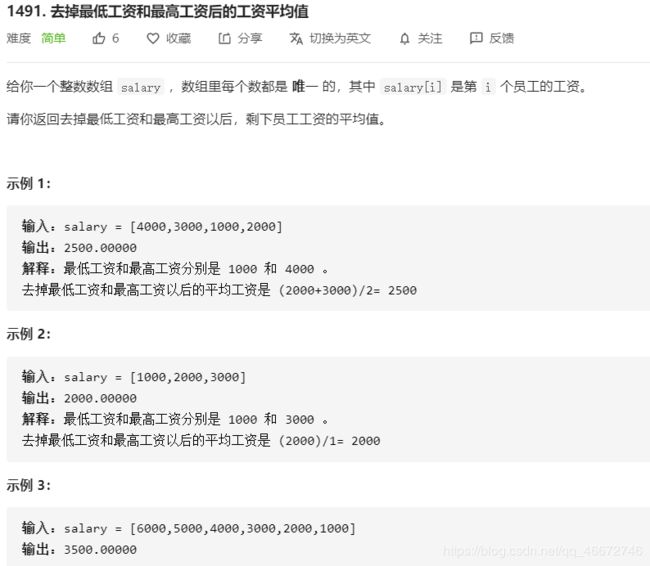
1491.去掉最低工资和最高工资后的工资平均值
class Solution {
public double average(int[] salary) {
double sum = 0;
Arrays.sort(salary);
for(int i=1; i<salary.length-1; i++){
sum += salary[i];
}
return sum/(salary.length-2);
}
}
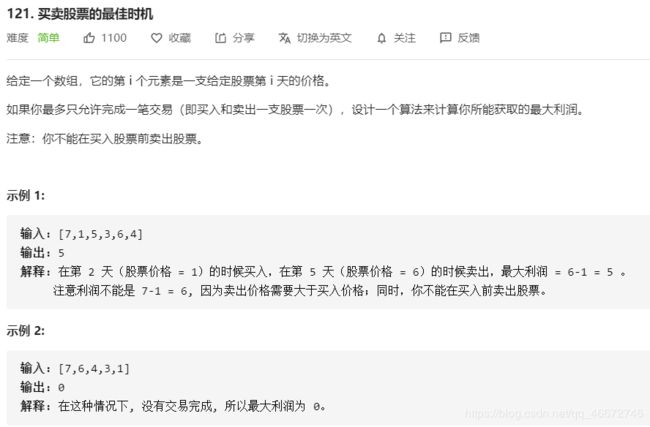
121.买卖股票的最佳时机
public class Solution {
public int maxProfit(int prices[]) {
int maxprofit = 0; //存储最大利润
for (int i = 0; i < prices.length - 1; i++) {
for (int j = i + 1; j < prices.length; j++) { //保证买卖时间的先后顺序
int profit = prices[j] - prices[i]; //计算第i天后的每一天和第i天价格的差值
if (profit > maxprofit) //找出最大差值
maxprofit = profit;
}
}
return maxprofit;
}
}
思路2:记录历史最低点,若不是最低点,则将其与先前找到的最低点相减、找到最大利润(不过好像有问题 比如:9,2,7,1,3不适用)
求出历史最低点(买入时机),依次求每个卖出时机的的最大差值,再从中取最大值。
public class Solution {
public int maxProfit(int prices[]) {
int minprice = Integer.MAX_VALUE;
int maxprofit = 0;
for (int i = 0; i < prices.length; i++) {
if (prices[i] < minprice){
minprice = prices[i];
}
else if (prices[i] - minprice > maxprofit){
maxprofit = prices[i] - minprice;
}
}
return maxprofit;
}
}
122.买卖股票的最佳时机II

我们必须确定通过交易能够获得的最大利润(对于交易次数没有限制)。为此,我们需要找出那些共同使得利润最大化的买入及卖出价格
思路1:
暴力法(官方给的代码 可 我运行后 超出时间限制):
这种情况下,我们只需要计算与所有可能的交易组合相对应的利润,并找出它们中的最大利润。
class Solution {
public int maxProfit(int[] prices) { //主
return calculate(prices, 0);
}
public int calculate(int prices[], int s) {
if (s >= prices.length) //数组长度小于s(s=0时数组为空) 没有股票 利润为0
return 0;
int max = 0; //多次交易后最终的最大利润
for (int start = s; start < prices.length; start++) { //遍历数组
int maxprofit = 0; //定义一次交易后的最大利润
for (int i = start + 1; i < prices.length; i++) { //遍历买入股票后的每一天
if (prices[start] < prices[i]) { //第i天股票价格大于买入时价格
int profit = calculate(prices, i + 1) + prices[i] - prices[start]; //计算此时利润
if (profit > maxprofit) //与之前的利润作比较 求出每一次交易最大利润
maxprofit = profit;
}
}
if (maxprofit > max) //多次交易后的最大利润
max = maxprofit;
}
return max;
}
}
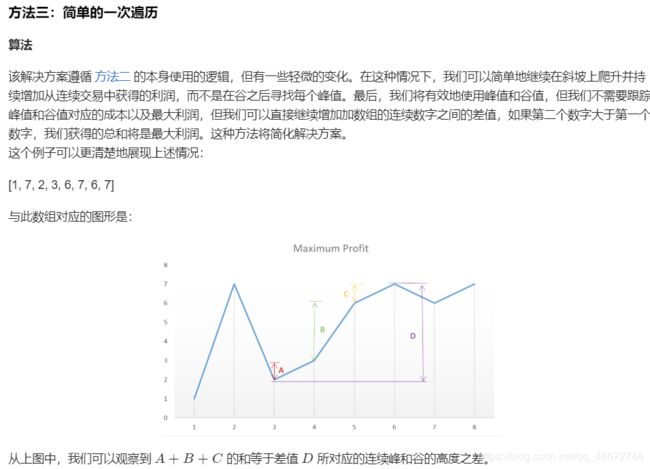
思路2:峰谷法:
连续的峰和谷
class Solution {
public int maxProfit(int[] prices) {
int i = 0;
int valley = prices[0]; //峰
int peak = prices[0]; //谷
int maxprofit = 0;
while (i < prices.length - 1) { //遍历数组
while (i < prices.length - 1 && prices[i] >= prices[i + 1]){ //找波谷
i++;
}
valley = prices[i]; //将所有的波谷值相加
while (i < prices.length - 1 && prices[i] <= prices[i + 1]){ //找波峰
i++;
}
peak = prices[i]; //将所有的波峰值相加
maxprofit += peak - valley;
}
return maxprofit;
}
}
class Solution {
public int maxProfit(int[] prices) {
int maxprofit = 0;
for (int i = 1; i < prices.length; i++) {
if (prices[i] > prices[i - 1])
maxprofit += prices[i] - prices[i - 1];
}
return maxprofit;
}
}
1018.可被5整除的二进制前缀(没懂)
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
bool* prefixesDivBy5(int* A, int ASize, int* returnSize)
{
int temp = 0;
*returnSize = ASize;
bool* ret = (bool*)malloc(ASize * sizeof(bool));
for (int i = 0; i < ASize; i++) {
temp = (temp << 1) + A[i]; //换算成十进制
temp = temp % 5;
if (temp == 0) { //判断是否能被5整除
ret[i] = true;
} else {
ret[i] = false;
}
}
return ret;
}
1502.判断能否形成等差数列

思路:
先排序,后看是否满足arr[i] * 2 = arr[i - 1] + arr[i + 1]
class Solution {
public boolean canMakeArithmeticProgression(int[] arr) {
Arrays.sort(arr);
for (int i = 1; i < arr.length - 1; ++i) {
if (arr[i] * 2 != arr[i - 1] + arr[i + 1]) {
return false;
}
}
return true;
}
}
605.种花问题

思路:
方法一:贪心
我们从左到右扫描数组 flowerbed,如果数组中有一个 0,并且这个 0 的左右两侧都是 0,那么我们就可以在这个位置种花,即将这个位置的 0 修改成 1,并将计数器 count 增加 1。对于数组的第一个和最后一个位置,我们只需要考虑一侧是否为 0。
在扫描结束之后,我们将 count 与 n 进行比较。如果 count >= n,那么返回 True,否则返回 False。
public class Solution {
public boolean canPlaceFlowers(int[] flowerbed, int n) {
int i = 0, count = 0;
while (i < flowerbed.length) { //遍历数组
if (flowerbed[i] == 0 && (i == 0 || flowerbed[i - 1] == 0) && (i == flowerbed.length - 1 || flowerbed[i + 1] == 0)) { //判断能否种花
flowerbed[i] = 1;
count++;
}
i++;
}
return count >= n;
}
}
1351.统计有序矩阵中的负数

思路:二分法
注意到题目中给了一个性质,即矩阵中的元素无论是按行还是按列,都以非递增顺序排列,可以考虑把这个性质利用起来优化暴力。已知这个性质告诉了我们每一行的数都是有序的,所以我们通过二分查找可以找到每一行中从前往后的第一个负数,那么这个位置之后到这一行的末尾里所有的数必然是负数了,可以直接统计。
class Solution {
public int countNegatives(int[][] grid) {
int count = 0, m = grid.length, n = grid[0].length; //m:有多少组,n:一组有多少个数
for (int i = 0; i < m; i++) { //一组一组遍历
int[] row = grid[i];
if (row[n - 1] >= 0){
continue;
} // 整行非负,跳过
if (row[0] < 0) { // 整行负数
count += (m - i) * n; // 后面的行也计入
break; // 无需再继续遍历
}
int first = _binarySearch(row); // 当前行二分查找第一个小于 0 的数的索引
count += n - first;
}
return count;
}
// 查找第一个小于 0 的数的索引
private int _binarySearch(int[] arr) {
int begin = 0, end = arr.length;
while (begin < end) {
int mid = begin + ((end - begin) >> 1);
if (arr[mid] >= 0) {
begin = mid + 1;
}
else { // 负数之后,还要再判断前一个不是负数(不太懂)
if (arr[mid - 1] >= 0) {
return mid;
}
end = mid;
}
}
return begin;
}
}