算法设计技巧: Primal-Dual
原始对偶(Primal-Dual)是一种求解优化问题的思想, 在凸优化和组合优化问题中有重要应用. 本文以线性规划问题为例解释原始对偶算法的设计思路, 进而介绍如何设计基于原始对偶的近似算法(一般用于求解NP-hard问题).
互补松弛条件
考虑线性规划的原始问题(P)和对偶问题(D)如下:
min c T x s.t. A x ≥ b x ≥ 0 (P) \begin{aligned} \min\ & c^Tx \tag{P}\\ \text{s.t. } & Ax \geq b\\ & x \geq 0 \end{aligned} min s.t. cTxAx≥bx≥0(P)
max b T y s.t. A T y ≤ c y ≥ 0 (D) \begin{aligned} \max\ & b^T y \tag{D}\\ \text{s.t. } & A^Ty \leq c \\ & y \geq 0 \end{aligned} max s.t. bTyATy≤cy≥0(D)
互补松弛条件(Complementary Slackness Condition)
- Primal complementary slackness conditions
x j > 0 ⇒ [ A T y ] j = c j x_j > 0\Rightarrow [A^Ty]_j = c_j xj>0⇒[ATy]j=cj - Dual complementary slackness conditions
y i > 0 ⇒ [ A x ] i = b i y_i > 0 \Rightarrow [Ax]_i = b_i yi>0⇒[Ax]i=bi
其中 [ ⋅ ] i [\cdot]_i [⋅]i是表达式的第 i i i个分量.
当互补松弛条件成立且 x x x和 y y y分别是原问题(P)和对偶问题(D)的可行解, 那么它们也是对应问题的最优解. 回顾线性规划的单纯形算法(Simplex Algorithm), 它从原问题(P)的一个可行解出发, 在满足互补松弛条件的前提下, 使得其对偶变量朝着对偶可行解的方向迭代. Primal-Dual的思想是从对偶可行解出发, 在满足互补松弛条件的前提下, 使得原始变量朝着可行解的方向迭代. 在经典的组合优化问题例如Maximal Flow, Minimum Cost Flow, Maximum Weight Matching等都有Primal-Dual算法的身影.
下面我们介绍如何利用Primal-Dual的思想设计近似算法.
松弛的互补松弛条件
设 x x x, y y y分别为(P)和(D)的可行解. 存在常数 α ≥ 1 , β ≥ 1 \alpha\geq 1, \beta \geq 1 α≥1,β≥1满足如下条件:
- Relaxed primal complementary slackness
x j > 0 ⇒ [ A T y ] j ≥ c j / α x_j > 0\Rightarrow [A^Ty]_j \geq c_j/\alpha xj>0⇒[ATy]j≥cj/α - Relaxed dual complementary slackness
y i > 0 ⇒ [ A x ] i ≤ β b i y_i > 0 \Rightarrow [Ax]_i \leq \beta b_i yi>0⇒[Ax]i≤βbi
基于Primal-Dual的近似算法从对偶可行解出发, 始终满足松弛的(Relaxed)互补松弛条件, 且朝着原问题可行解的方向迭代.
由于 x x x和 y y y分别是(P)和(D)的可行解, OPT为原问题最优解的目标值. 此外, 根据上述 松弛的 互补松弛条件, 我们有
c T x ≤ α ( A T y ) T x = α y T ( A x ) ≤ α β y T b = α β b T y ≤ α β ⋅ OPT . c^Tx \leq \alpha(A^Ty)^T x = \alpha y^T(Ax) \leq \alpha \beta y^Tb = \alpha \beta b^T y \leq \alpha\beta\cdot \text{OPT}. cTx≤α(ATy)Tx=αyT(Ax)≤αβyTb=αβbTy≤αβ⋅OPT.
换句话说, 上述算法得到的目标值不超过最优值的 α β \alpha \beta αβ倍. 当 α β \alpha\beta αβ越小, 算法的解与最优解越近.
基于Prima-Dual的近似算法
以最小化问题为例, 基于Primal-Dual的近似算法框架如下:
- 把问题用整数规划建模, 然后考虑其松弛的线性规划问题(P)以及对应的对偶问题(D).
- 初始化对偶可行解 y y y以及原始问题的不可行解 x x x. (一般来说, 初始化时 x = 0 , y = 0 x=0, y=0 x=0,y=0.)
- 用某种方式增加 y i y_i yi直到某个约束 [ A y ] j = c j / α [Ay]_j = c_j /\alpha [Ay]j=cj/α且始终保持 y y y的可行性. 然后根据对偶约束增加 x i x_i xi的值直到 x x x成为原问题(整数规划问题)的可行解.
- 对偶问题的解是OPT的下界. 算法的近似比是 α β \alpha\beta αβ.
(更多细节参考这里)
Set Cover
Set Cover是一个经典的组合优化问题. 我们已知:
- 元素的集合 E = { 1 , 2 , … , n } E=\{1, 2, \ldots, n\} E={1,2,…,n}
- m m m个集合 S 1 , S 2 , … , S m S_1, S_2, \ldots, S_m S1,S2,…,Sm, 其中 S j ⊆ E S_j\subseteq E Sj⊆E
- 每个集合的费用 c j c_j cj, j = 1 , 2 , … , m j=1,2, \ldots, m j=1,2,…,m
目标是找到一些集合 S j 1 , S j 2 , … , S j k S_{j_1}, S_{j_2},\ldots, S_{j_k} Sj1,Sj2,…,Sjk使得它们覆盖 E E E, 即 ∪ i = 1 k S j i = E \cup_{i=1}^k S_{j_i} = E ∪i=1kSji=E, 且总成本最低.
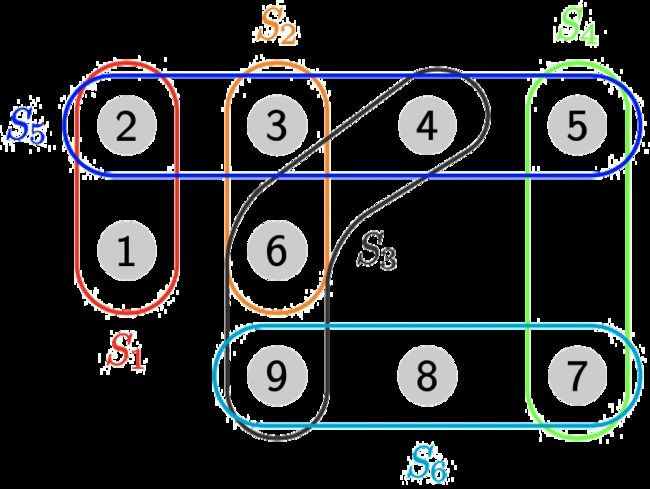
例 如下图所示 E = { 1 , 2 , … , 9 } E=\{1, 2, \ldots, 9\} E={1,2,…,9}, S = { S 1 , S 2 , … , S 6 } \mathcal{S} = \{S_1, S_2, \ldots, S_6\} S={S1,S2,…,S6}. 根据定义, C = { S 1 , S 2 , S 5 , S 6 } \mathcal{C} = \{S_1, S_2, S_5, S_6\} C={S1,S2,S5,S6}是一个set cover. 当给定每个集合 S j S_j Sj的权重时, 我们的目标是要找到一个总成本最低的set cover.
整数规划
令 S = { S 1 , S 2 , … , S m } \mathcal{S} = \{S_1, S_2, \ldots, S_m\} S={S1,S2,…,Sm}. ∀ S ∈ S \forall S\in \mathcal{S} ∀S∈S, 定义决策变量 x S ∈ { 0 , 1 } x_S\in \{0, 1\} xS∈{0,1}, 代表是否选择 S S S. 上述问题可以描述成如下整数规划.
min ∑ S ∈ S c S x S s.t. ∑ S ∋ e x S ≥ 1 , ∀ e ∈ E x S ∈ { 0 , 1 } \begin{aligned} \min\ & \sum_{S\in \mathcal{S}}c_Sx_S \\ \text{s.t. } & \sum_{S\ni e} x_S \geq 1, \quad \forall e\in E \\ & x_S \in \{0, 1\} \end{aligned} min s.t. S∈S∑cSxSS∋e∑xS≥1,∀e∈ExS∈{0,1}
其LP relaxation的对偶问题如下:
max ∑ e ∈ E y e s.t. ∑ e ∈ S y e ≤ c S , ∀ S ∈ S y e ≥ 0 , ∀ e ∈ E . \begin{aligned} \max\ & \sum_{e\in E} y_e \\ \text{s.t. } & \sum_{e\in S}y_e \leq c_S, \quad \forall S\in \mathcal{S} \\ & y_e \geq 0, \quad \forall e\in E. \end{aligned} max s.t. e∈E∑yee∈S∑ye≤cS,∀S∈Sye≥0,∀e∈E.
互补松弛条件
- Primal complementary slackness
x S > 0 ⇒ ∑ e ∈ S y e = c S x_S > 0 \Rightarrow \sum_{e\in S}y_e = c_S xS>0⇒e∈S∑ye=cS - Dual complementary slackness
y e > 0 ⇒ ∑ S ∋ e x S = 1 y_e > 0\Rightarrow \sum_{S\ni e}x_S = 1 ye>0⇒S∋e∑xS=1
思路: Relax对偶互补条件: 存在 β > 1 \beta>1 β>1, 满足
y e > 0 ⇒ ∑ S ∋ e x S ≤ β . y_e > 0 \Rightarrow \sum_{S\ni e}x_S \leq \beta. ye>0⇒S∋e∑xS≤β.
Primal-Dual算法
- 初始化 x S = 0 , ∀ S ∈ S x_S=0, \forall S\in\mathcal{S} xS=0,∀S∈S, y e = 0 , ∀ e ∈ E y_e=0,\forall e\in E ye=0,∀e∈E.
- 如果存在 e ∈ E e\in E e∈E未被覆盖, 则增加 y e y_e ye直到存在 S ∈ S S\in \mathcal{S} S∈S使得 ∑ e ∈ S y e = c S \sum_{e\in S} y_e = c_S ∑e∈Sye=cS, 然后把所有满足条件的 S S S添加到结果中(即, x S = 1 x_S=1 xS=1), 并把相应的元素标记未已覆盖.
说明 上述 y e y_e ye的取值可以在区间 [ 0 , max c S ] [0, \max c_S] [0,maxcS]通过二分查找得到.
近似比
令 f e = ∣ { S j ∣ e ∈ S j } ∣ f_e = |\{S_j | e \in S_j\}| fe=∣{Sj∣e∈Sj}∣, 代表元素 e e e在所有 S j S_j Sj中出现的次数. 令 f = max f e f = \max f_e f=maxfe, 我们有 ∑ S ∋ e x S ≤ f \sum_{S\ni e}x_S \leq f ∑S∋exS≤f. 因此, 该算法的近似比为 f f f, 即 ALG ≤ β ⋅ OPT \text{ALG}\leq \beta \cdot \text{OPT} ALG≤β⋅OPT.
Python实现
class SetCoverPD(object):
""" 基于Primal-Dual的近似算法求解Set Cover问题.
"""
def __init__(self, m, sets, costs):
"""
注意: 输出参数的数值必须是整数.
:param m: 元素个数. 元素的编号从0开始, e.g. 0, 1, ..., m-1
:param sets: 元素(下标)的集合, list of sets, e.g. [{0, 2}, {1, 2, 3, 6}, {3, 4, 5}, {2, 4, 6}]
:param costs: 每个元素集合的cost, e.g. [2, 3, 4, 1]
"""
self._m = m
self._sets = sets
self._costs = costs
self._result = [] # 计算结果: 保存结果集合在sets中的编号
self._y = [0] * self._m # 对偶决策变量
def solve(self):
"""
Primal-Dual算法.
"""
uncovered_elements = set(range(self._m))
ub = max(self._costs)
while uncovered_elements:
# 如果存在未被覆盖的元素i, 通过二分查找y[i]的值使得它满足条件:
# y(S)=c(S), for some S 包含元素i. (称S为tight set.)
i = uncovered_elements.pop()
tight_sets = self._binary_search(i, 0, ub)
# 把关于i的所有tight sets添加到结果集
for ts in tight_sets:
uncovered_elements -= self._sets[ts]
self._result.append(ts)
def _is_some_set_satisfied(self, i):
""" 给定i(已知y[i]), 判断是否存在集合S满足y(S)>=c(S),
其中y(S)代表S中元素对应y值之和, c(S)代表集合S的cost.
"""
for j in range(len(self._sets)):
set_j = self._sets[j]
if i not in set_j:
continue
sum_y = sum([self._y[k] for k in set_j])
if sum_y >= self._costs[j]:
return True
return False
def _binary_search(self, i, lb, ub):
"""
用二分法查找y[i]使得y(S) = c(S) for some S (S称为tight set)
:param i: 元素的下标
:param lb: y_i的下界
:param ub: y_i的上界
:return: list of tight sets
"""
if ub - lb <= 1:
self._y[i] = ub
return self._get_tight_sets(i)
mid = (lb + ub) // 2
self._y[i] = mid
if not self._is_some_set_satisfied(i):
return self._binary_search(i, mid, ub)
else:
return self._binary_search(i, lb, mid)
def _get_tight_sets(self, i):
"""
已知y[i], 找到所有tight sets(满足y(S)=c(S)).
"""
tight_sets = []
for j in range(len(self._sets)):
set_j = self._sets[j]
if i not in set_j:
continue
sum_y = sum([self._y[k] for k in set_j])
if abs(sum_y - self._costs[j]) < 1e-6:
tight_sets.append(j)
return tight_sets
def print_result(self):
print("solution:", [self._sets[i] for i in self._result])
print("total cost:", sum([self._costs[i] for i in self._result]))
if __name__ == '__main__':
sc = SetCoverPD(9, # m
[{0, 1}, {2, 5, 8}, {3, 5}, {4, 6}, {1, 2, 3, 4}, {6, 7, 8}], # sets
[4, 2, 5, 7, 8, 1] # costs
)
sc.solve()
sc.print_result()