2019年上海市数学建模讲座(3)微分方程建模方法
第三场微分方程建模讲座笔记
主讲人:董程栋,上海财经大学数学学院

微分方程:
定义:联系着自变量,未知函数与它的导数之间的关系式
物体冷却过程中的数学模型
牛顿冷却定律:物体温度变化速度与物体和介质温度的差值成正比
学到:
第一,找到相应的背景知识
第二,掌握微分方程的知识
动态模型:
定义:描述对象特征随着时间(或者空间)的演变过程
分析,预报,控制对象的手段
常微分方程
微分方程分为常微分方程和偏微分方程
常微分方程:自变量只有一个的微分方程
常微分方程建模过程:
1.简化假设
2,实际情况:函数和变化率
3.内在规律建方程
减肥模型
分析:能量守恒
建立模型
(以上照片如果侵权,请联系笔者删除)
看竞赛真题
2001年美赛斑马贻贝,数量过多有害
【1】讨论影响传播的因素
【2】利用数据模拟斑马贻贝的增长情况
想到:自然界生物增长模型
阻滞增长模型 logistic模型
最重要的假设是最大容量是多少
一般形式是微分方程,得到导数是钟形图形
我们需要看图形,根据数据,绘制斑马贻贝的模型得到差不多的增长图像
1996年竞赛A题:最优捕鱼策略
捕捞强度系数和自然死亡率
单位时间内捕捞量与鱼群数量的比例系数
规划问题
微分方程模型一般是一部分,一道题中的
2005A题:长江水质综合评价
1评价定量评价,分析水质污染情况 2.污染源有哪些
四个指标:溶解氧,高猛酸盐指数,氨氮,ph
1.指标的问题:
有的越大越好,有的越小越好。
有的一项指标会覆盖其他指标,比如氨氮是六级,溶解氧很高,也是污水,水质不好
还有:量纲不同,数据大小不同
2.数据的标准化处理
ph值的谷型处理
|ph-7|除以一个差
DO值的归一化处理
NH3-N归一化处理
n减去最小值,整体除以最大值减去最小值这个整体
3.综合指标的确定
采用动态加权法
给定一个欧米伽,作用是让数据分散化,手机上有照片
是否可以用层次分析法来求四个参数的权重?
层次分析法的一致性检验 不一定能通过
17个观测点28个排序结果
决策论中的borda数法决定决策方案
上面是第一问
思考:我们要学习的是对数据的处理方法
第二问,看污染物 的问题
分为六段,逐段分析
一维水质模型
污染物分布浓度,断面均匀,平均流速,其中k是污染物降解系数
怎么用呢?
江段AB距离d,n个排污口
排污口的流量,平均流速,污染物浓度
和江段干流的上述三个参数,用大写表示
找到干流和排污口和上游的关系
污染物排放量的确定方法
排污量的上界值
假设AB段内所有排污在一个点A,降解在一个位置B
排污量的下界值
假设排污口都在B点
平均相对排污量
取中值作为平均
第二问用的是一维水质模型:常微分方程解决了这个问题
第三问
线性多元回归
第四问,控制污水的比例
用的主要是回归
总结这道题目:
计算排污的上界值和下界值,从而计算相对平均值,计算整体的排污量,这是一维水质模型,常微分方程的作用
下一道竞赛题
2003年A题 SARS 传播
提供一个早期的模型,评判
建立自己的模型,预测预防控制信息的模型
传染病模型回顾(笔者自己查找资料)

模型一:已感染人数(病人)

模型四:移出者SIR模型
传染病模型部分来源于
http://www.mcm.dept.ccut.edu.cn/sort.asp?4V3z3P2z2z2J2.html
评价之前的模型:
一:优点
抓住主要特征
对比
容易理解
对参数挑选
二:缺点
缺乏一般原则和算法
第二问
建立自己的模型
模型的改进
四类:死亡的人包括进来
病人的变化,右边是传染的,治疗好的,死亡的
还有死亡的
建立常微分方程组
需要离散,得到递推关系,差分方程
每个sars病人传染的人数,确定的原则是:新增的病人除以当天的感染人数
用指数曲线进行回归拟合
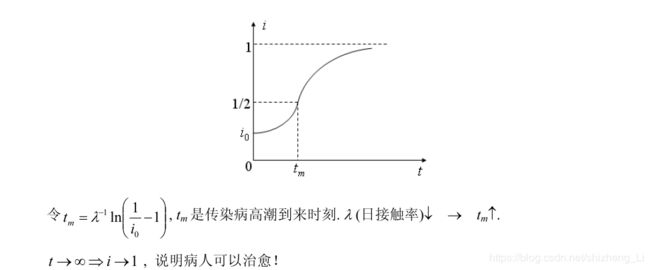
得到随时间变化的关系,用图像来表示
第三问:收集Sars 对经济某方面影响的数据,建立模型
老师补充:善于运用现成的模型,加上自己的创新点
第三问影响可能是好的,不仅仅是坏的结果。
建模数值解法的基本思想
【1】euler折现法
或者称为矩形法
利用taylor展开
【2】化导数成为差商
两者都能得到差分方程
输入参数,可以求得差分的方程结果
【总结】
微分方程的偏微分部分是竞赛中常考点。熟悉一些基本的微分方程的模型,但是具体问题具体分析。比如人口模型,传染病模型需要掌握。
备注:以上是笔者参加上海大学数学建模培训时记录的笔记。中间包含部分笔者查找的资料。