zkw（张昆玮）线段树（单点更新）

zkw线段树特点：

非递归，代码简短，结合位运算速度快

结构：

我们可以用一个一维数组c[]来储存数据信息

接下来详细介绍单点更新和区间和求法：

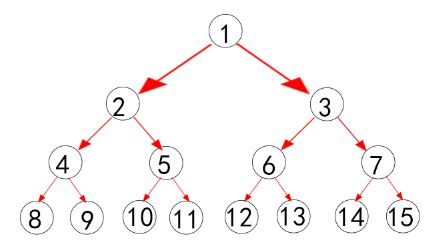
假设需要处理的数组为a[n]，则上图叶子数至少为n + 2（其中第一片叶子跟最后一片叶子是不能储存数据的，后面解释），比如说如果n = 2，那只需要把c[]数组开到8；但3 <= n <= 6都要把c[]数组开到16，依次类推。所以叶子数M可以这样求：for(M = 1; M < n + 2; M <<= 1); 则整个c[]就需要2*M个空间。

然后是把a[n]（这里设n = 6）里的元素存到c[]里面，准确地说是存到叶子里面，以上图举例，从第二片叶子9开始；依次把a[0] ~ a[n]存入c[9] ~ c[14]；（即是a[]下标后移一位 + M）当然还要往上更新，相当于update，后面讲。

假设把所有信息都存进去了，那每个结点的值表示以该结点为根的所有叶子之和。比如结点3的值c[3] = c[12] + c[13] + c[14] + c[15]。即c[3] = a[3] + a[4] + a[5] + 0（空叶子的值定义为0）

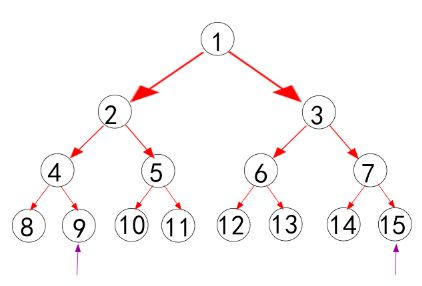
对于区间求和，比如我们要求a[1] ~ a[5]的和，那就把下标后移一位，即求[2, 6]的和。那我们可以通过left + M - 1（left在这里表示2，M为叶子数），right + M +1直接定位[2, 6]对应于c[]的开区间(9, 15)，这里注意a[]下标不能从0开始，因为定不了左开区间（0 + M - 1 = 7 不是叶子），所以a[]数组下标要后移一位；上面讲的要从第二片叶子开始储存的原因也是这样；右边同理，因此叶子最少要n + 2；也即是说如果n = 1023，那M就要不小于n + 2，就只能是M = 2^11了，基本属于最坏情况。

我们的目标是求c[10] ~ c[14]之和，先放代码：

int Query(int l, int r) //[l, r]
{
    int ans = 0;
    for(l = l + M - 1, r = r + M + 1; l^r^1; l >>= 1, r >>= 1){
        if(~l&1) ans += c[l^1]; //l为偶数
        if(r&1) ans += c[r^1]; //r为奇数
    }
    return ans;
}

即是：

一）ans = 0；

二）如果left为偶数，ans就加上left的右结点的值；如果right为奇数，ans就加上right的左结点的值；

三）left 和 right 分别除以2后，如果left 与 right相邻，就退出循环；否则回到第二步。

这样做可以求区间和的原理手动算算都能明白~

对于更新操作，比如要把a[2]的值修改为v，同样下标右移一位，即把c[3 + M] = c[11] 的值修改为v；接下来往上更新。这步不难想到：

void Update(int p, int v)
{
    p += M;
    val[p] = v;
    while(p > 1){
        p >>= 1;
        val[p] = val[p<<1] + val[p<<1|1];
    }
}

非常简洁！

用一道题练手，HDU 1754 ：点击打开链接

这是求区间最值的，相同的道理

I Hate It

Time Limit: 9000/3000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 47267    Accepted Submission(s): 18506

Problem Description

很多学校流行一种比较的习惯。老师们很喜欢询问，从某某到某某当中，分数最高的是多少。
这让很多学生很反感。

不管你喜不喜欢，现在需要你做的是，就是按照老师的要求，写一个程序，模拟老师的询问。当然，老师有时候需要更新某位同学的成绩。

 

Input

本题目包含多组测试，请处理到文件结束。
在每个测试的第一行，有两个正整数 N 和 M ( 0 学生ID编号分别从1编到N。
第二行包含N个整数，代表这N个学生的初始成绩，其中第i个数代表ID为i的学生的成绩。
接下来有M行。每一行有一个字符 C (只取'Q'或'U') ，和两个正整数A，B。
当C为'Q'的时候，表示这是一条询问操作，它询问ID从A到B(包括A,B)的学生当中，成绩最高的是多少。
当C为'U'的时候，表示这是一条更新操作，要求把ID为A的学生的成绩更改为B。

 

Output

对于每一次询问操作，在一行里面输出最高成绩。

 

Sample Input

5 6 1 2 3 4 5 Q 1 5 U 3 6 Q 3 4 Q 4 5 U 2 9 Q 1 5

 

Sample Output

5 6 5 9

Hint

Huge input,the C function scanf() will work better than cin

#include 
#include 
#include 
#include 
#define N 200005
#define INF (1<<30)
#define MAX(x, y) ((x) > (y) ? (x) : (y))
int *val;
int M;

void Update(int p, int v)
{
    p += M;
    val[p] = v;
    while(p > 1){
        p >>= 1;
        val[p] = MAX(val[p<<1], val[p<<1|1]);
    }
}

int Query(int l, int r) //[l, r]
{
    int ans = -INF;
    for(l = l + M - 1, r = r + M + 1; l^r^1; l >>= 1, r >>= 1){
        if(~l&1) ans = MAX(val[l^1], ans); //l为偶数
        if(r&1) ans = MAX(val[r^1], ans); //r为奇数
    }
    return ans;
}

int main()
{
    //freopen("in.txt", "r", stdin);
    int n, m, i, a, p;
    char str[3];
    while(scanf("%d%d", &n, &m) != EOF)
    {
        for(M = 1; M < n + 2; M <<= 1);
        val = (int *)malloc(sizeof(int) * M * 2);
        memset(val, 0, sizeof(val));
        for(i = 0; i < n; i++){
            scanf("%d", &a);
            Update(i + 1, a);
        }
        scanf("%d", &m);
        while(m--)
        {
            scanf("%s", str);
            scanf("%d%d", &p, &a);
            if('U' == str[0]) Update(p, a);
            else printf("%d\n", Query(p, a));
        }
        free(val);
    }
    return 0;
}

用这样的方法做区间更新，暂时没有悟透PPT的思想，弄懂了再上，以下是原文链接：

点击打开链接