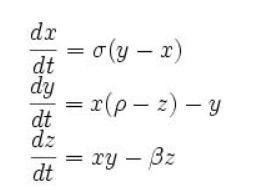python解常微分方程组

美国气象学家洛伦兹（E.N.Lorenz）是混沌理论的奠基者之一。20世纪50年代末到60年代初，他的主要工作目标是从理论上进行长期天气预报研究。他在使用计算机模拟天气时意外发现，对于天气系统，哪怕初始条件的微小改变也会显著影响运算结果。随后，他在同事工作的基础上化简了自己先前的模型，得到了有3个变量的一阶微分方程组，由它描述的运动中存在一个奇异吸引子，即洛伦兹吸引子，方程如下。

三个方程定义了三维空间中的各个坐标点上度速度矢量，其中ρ、σ、β为常数，不同的参数可以算出不同的轨迹：x(t)、y(t)、z(t)。当参数为某些值时，轨迹出现混沌现象。即最小的初值差别也会显著地影响运动轨迹。

import pylab as pl
import numpy as np
from scipy import integrate
from scipy.integrate import odeint

#%fig=洛伦茨吸引子：微小的初值差别也会显著地影响运动轨迹
from scipy.integrate import odeint 
import numpy as np 

def lorenz(w, t, p, r, b): #❶
    # 给出位置矢量w，和三个参数p, r, b计算出
    # dx/dt, dy/dt, dz/dt的值
    x, y, z = w.tolist()
    # 直接与lorenz的计算公式对应 
    return p*(y-x), x*(r-z)-y, x*y-b*z

t = np.arange(0, 30, 0.02) # 创建时间点 
# 调用ode对lorenz进行求解, 用两个不同的初始值 
track1 = odeint(lorenz, (0.0, 1.00, 0.0), t, args=(10.0, 28.0, 3.0)) #❷
track2 = odeint(lorenz, (0.0, 1.01, 0.0), t, args=(10.0, 28.0, 3.0)) #❸
#%hide
from mpl_toolkits.mplot3d import Axes3D
fig = pl.figure()
ax = Axes3D(fig)
ax.plot(track1[:,0], track1[:,1], track1[:,2], lw=1)
ax.plot(track2[:,0], track2[:,1], track2[:,2], lw=1);

洛伦茨吸引子：即使微小的差别也会显著地影响运动轨迹

[1]洛伦茨吸引子介绍参考：http://bzhang.lamost.org/website/archives/lorenz_attactor

[2]《python科学计算》（张若愚著）