算法的时间复杂度的计算是一个可以无限深入的课题。但是对于程序员来说,能够大概的评估出复杂度就已经足够用了。
在算法这个系列之前的几篇文章里,介绍了算法的使用和原理,但是我故意的将复杂度的介绍没有写上去。有两个原因:第一是这个算法复杂度介绍起来还是比较麻烦,一下子介绍不完,写在一篇里不太合适;第二是还没有想好怎么写。
现在终于可以想得差不多了,可以开工写写。我的本意是尽量写得简单易懂,但是不把概念和内容简化。这看起来颇有难度。如果说你读完了本文,还是觉得没懂。欢迎提出意见,让我能够进步一下,写得更简单一些。
什么是 算法复杂度
首先,作为一个算法来说,有两个特性:
- 它用来处理一定规模的数据
- 它处理数据 需要时间
有了这两个基础的认知,我们可以简单的认为:随着数据规模的变化,算法处理数据需要的时间也会变化。
算法时间复杂度就是:用一个公式来表示,这个数据规模和时间变化的关系。
比如:
假设一个算法 F,一个数据集 N;
- 当 N 中包含 10个元素时, 使用算法 F 进行处理,需要花费 5s。
- 当 N 中包含 30个元素时,使用算法 F 进行处理,需要花费 15s。
- 当 N 中包含 300 个元素时,使用算法 F 进行处理,需要花费 150s。
- ……
可以看到,随着数据规模的增长,算法处理需要的时间也在变化。如果我们想要表达这个时间变化的趋势和数据集N的关系的话,我们假设这个关系是 \(T(N)\) 我们可以写下面的一个算式:
\[T(N) = F(N)\]
这里的 \(T(N)\) 表示了一个算法对于数据集N需要使用的时间的精确计算。
Big O 表示法
在实际上,精确计算公式是不可能被统计计算出来的,因为不同的语句,不同的操作,耗费的时间也是不一样。所以,在实际应用中,我们不需要精确计算,只需要一个公式,来表达 时间花费和数据集大小的渐近关系。
所以,在描述算法的时候,一般采用 大O(Big-O notation)表示,又称为渐进符号,
Big-O 是用于描述函数渐近行为的数学符号。更确切地说,它是用另一个(通常更简单的)函数来描述一个函数数量级的渐近上界。 -- 《维基百科》
上面的解释太玄幻。
其实简单来说,一个函数是几个项的和,每个项都能被归入到一个数量级,比如(平方、立方)。当数据集(自变量)趋于无穷大时,数量级大的变化太大,造成了数量级小的部分对函数结果的影响小到可以被忽略。
所以,我们就简单的使用数量级大的部分来替代整个函数,来简化表达。
比如:
\[T(N) = 2N^3 + N^2 + 1024\]
这个 \(T(N)\) 表达了某个算法的时间复杂度。
我们可以将这个等式分为三个项,按照数量级大小降序:
- A: \(2N^3\)
- B: \(N^2\)
- C: \(1024\)
我们对N取几个值来分别看一下 A 、B 、C 三个部分的值:
- 当N=10;A=2000,B=100,C=1024
- 当N=100;A=2000000,B=10000,C=1024
- 当N=1000;A=2000000000(
20亿),B=1000000(100万),C=1024 - 当N=10000;A=2000000000000(
2兆),B=100000000(1亿),C=1024 - 就不计算了吧……
可以看到,当数据集变大的时候,数量级大的部分增长的速度远远超过数量级小的部分。当N增大时,A占主导,B 和 C 两个部分的值相对于A部分来说,对结果的影响就可以忽略不计了。
然后,再看 A 部分,决定 A 部分大小的是 \(n^3\)。当我们要表达一个渐进关系的时候,常数并不影响这个关系的表达,所以 A 部分中的 常数就可以忽略。
最终,变成了下面:
\[T(N) = O(N^3)\]
这个 \(O(N^3)\) ,就是算法的时间复杂度。
TIPS: 上面的例子中,A部分常数是 2。可以放心的忽略。但如果是常数是 \(10^3\),忽略的话,结果就是错误的了。所以要对可能的大常数敏感。
计算代码的时间复杂度
明白了如何表示算法的复杂度。那如何计算复杂度呢?
简单计算
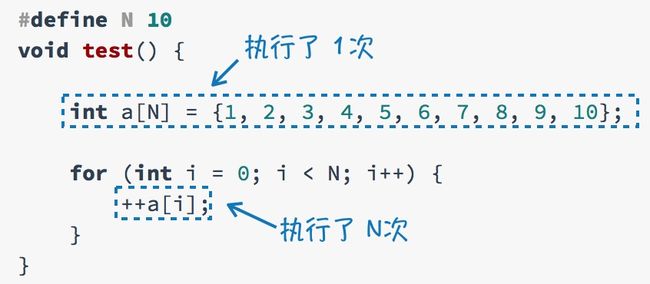
给出一个段简单的代码:将数组中每个元素的值加1。
我们分析它的语句执行的次数:
所以这里的时间复杂度是:
\[T(N) = n + 1 \to O(n)\]
冒泡排序分析
再来一个例子: 计算冒泡排序的算法复杂度
void sort(int *a, int len) {
for (int i = 0; i < len; i++) {
int min = i;
for(int j = i; j< len; j++){
if (a[j] < a[min]) // 比较动作
min = j;
}
swap(a, min, i);
}
}
对于基于比较的排序算法来说,我们在计算复杂度的时候,是计算比较了多少次。
- 第一次循环,比较了 N次;
- 第二次循环,比较了 N-1次;
- 第三次循环,比较了 N-2次;
总的比较次数就是 \(N + (N-1) + (N-2) + \ldots + 1 \),就是N的阶加。根据阶加公式可得:
\[ N\sim\quad = \frac {n(n+1)} 2 \Rightarrow O(n^2)\]
那么,冒泡排序的时间复杂度就是 \(O(n^2)\)。
更复杂的有什么?
在上面的两个例子中, 算法是稳定的。什么叫稳定呢? 就是不管数据集的内容是什么样的,以什么方式来组合,算法都是以这个复杂度来运行。
拿冒泡排序来说,不管给到的原始数组是排好序的、倒序的、乱序的,比较次数都是一样的,不存在算法的最好情况和最坏情况,这样的算法叫做稳定算法。
但是比如像 快速排序、堆排序 都是不稳定的算法。因为这类算法依赖于原始数据集的内容和其内容的组合方式。例如快速排序,如果原始数组是一个接近有序的,那么它的速度会快很多,如果原始数组是倒序的,那么快排的性能会急剧的恶化。而且,快排的效率还依赖于基准数的选择。
但是,对于数据集的分析这件事情,实在是太难了,远远超过了普通程序员的能力(包括我?),所以,这里我们就不再做数据的分析了。如果以后,我能说明白的时候,再写一篇另外的。
实例分析:快速排序复杂度
快排的文章详见 这里。快排几乎是使用最广泛的排序了,所以用它来做例子很合适。
同冒泡排序一样,快速排序是比较排序算法。我们只计算他比较的次数。
假设 n 是要排序的数据集规模,d 是递归的深度。
最好的情况
观察法
每一次递归都能分成两个子数组,大小 \(\le \frac n 2\),这样,递归的深度是最小的,就有:\(2^d = n\) ,那么容易知道,递归深度是: \(d = \log_2n\) 。在每一层的递归中,快排都要将所有的元素比较一遍,所以每一层的比较次数为 \(n\) 。那么,整体的比较次数为 \(n \cdot \log_2n\) , 那么,时间复杂度就是 \(O(n\cdot \log n)\) 。
推理法
有一个东东叫 主定理,这个东西广泛用在了递推分治算法的复杂度计算上,具体就不说了,大家自己上 Wikipedia 上看吧。这里,我们用它来进行推导。
假设时间复杂度是 \(T(n)\) ,那么,很明显, \(T(1) = T(0) = O(1)\)
快排中的分治算法符合主定理的递推关系式,所以有:
\[T(n) = 2T( \frac n 2 ) + O(n)\]
假定:
\[f(n) = O(n) = \Theta(n^{\log_22} \log^kn)\]
可得 \(k = 0\) ;符合 主定理的第二种情形。
可得:
\[T(n) = \Theta(n\log_22 \cdot \log n) \Rightarrow O(n\cdot \log n)\]
最坏的情况
每一次递归,划分出两个部分,一个部分中元素个数为0,另一个部分中,为 \(n-1\) ,这样,就需要递归 \(n\)次,每一层递归都需要将所有元素比较一次,那么整体的比较次数就是 \(n^2\) 。那么,时间复杂度就是 \(O(n^2)\) 。
平均情况
平均情况推算下来稍有点麻烦。如果我的推论讲得不清楚,大家只需要记住:
在平均的情况下,快排的算法复杂度和其在最好的情况下是一样的,都是 \(O(n\cdot \log n)\) 。
区别在于Big-O中隐藏的常量会大一点。
平均情况,就是在递归划分数组的过程中,有好的情况,有坏的情况。我们将两种情况极端化,即:使用最好的情况和最坏的情况,在递归树上交替出现,来观察算法的变化。
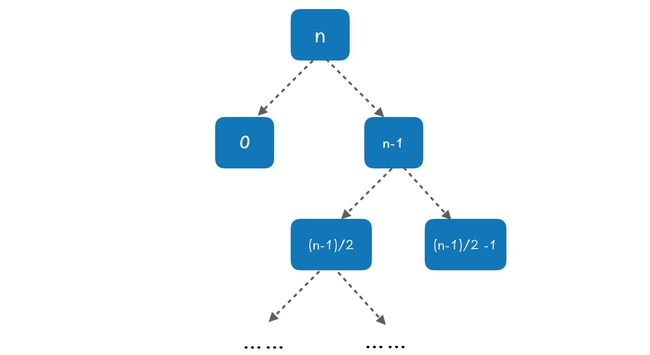
在根节点书,并划分出两个子数组: 0 和 n-1,这是最坏情况。在下一层,划分的大小为 \(\frac {n-1} 2\) 和 \(\frac {n-1} 2 -1\)。
这样每两层递归,会产生三种情况的组合:0、\(\frac {n-1} 2\) 和 \(\frac {n-1} 2 -1\) 。这个组合的划分代价为 \(O(n) + O(n-1) + O(1) = O(n)\) 。可以注意到,这个代价和平等划分的每次递归的时间是一样的!坏情况产生的代价被好的情况吸收。
区别在于,这种划分的方法会使得递归树变深,也就是常数会变得大一点,而最后的结果依然是 \(O(n\cdot \log n)\) 。
如果想要用数学的方式将其推导出来,也不是特别难,这个在 《算法导论》中有非常严谨的推论和计算,这里面涉及到了非常多的数学知识:求和公式、随机指标变量、调和级数、数学期望等等,一篇博文,不能覆盖全面,为了不误导读者,如果有兴趣,强烈建议,去读《算法导论》。