使用 pandas 进行数据预处理

1. 合并数据

1.1 堆叠合并

  堆叠就是简单地把两个表拼在一起，也被称作轴向连接、绑定或连接。依照连接轴的方向，数据堆叠可以分为横向堆叠和纵向堆叠。

1.1.1 横向堆叠

  横向堆叠，即将两个表在 y 轴方向拼接在一起，即左右拼接。可以使用 concat 函数完成。

pandas.concat(objs, axis=0, join='outer', ignore_index=False, keys=None, levels=None, 
			names=None, verify_integrity=False, sort=False, copy=True) 

concat 函数官方文档

concat 函数常用参数说明

参数名称	说明
objs	接收多个 Series、DataFrame、Panel 的组合。表示参与连接的 pandas 对象的列表的组合。
axis	接收 0 或 1。表示轴向。0：x 轴，纵向堆叠；1：y 轴，横向堆叠。默认为 0。纵向堆叠。
join	接收 inner 或者 outer。表示其他轴上的索引是按交集（inner）还是并集（outer）进行合并。默认为 outer。

# 索引完全相同时横向堆叠
import numpy as np
import pandas as pd
from sqlalchemy import create_engine

engine = create_engine('mysql+pymysql://root:123456@localhost:3306/testdb?charset=utf8')
detail = pd.read_sql('meal_order_detail1',con=engine)
df1 = detail.iloc[:,:10]    # 取出detail前10列数据
df2 = detail.iloc[:,10:]    # 取出detail后9列数据
print('df1的大小为%s，df2的大小为%s。'%(df1.shape,df2.shape))
print('内连接合并后数据框大小为：',pd.concat([df1,df2],axis=1,join='inner').shape)
print('外连接合并后数据框大小为：',pd.concat([df1,df2],axis=1,join='outer').shape)

1.1.2 纵向堆叠

  纵向堆叠是将两个数据表在 x 轴方向拼接，即上下拼接。可以使用 concat 函数和 append 方法。但是 append 方法的前提是两张表的列名需要完全一致。

DataFrame.append(self, other, ignore_index=False, verify_integrity=False, sort=False) 

append 函数官方文档

# 表名完全相同时的concat纵向堆叠
df3 = detail.iloc[:1500,:]       # 取出detail前1500行数据
df4 = detail.iloc[1500:,:]       # 取出detail的1500行后的数据
print('df3的大小为%s，df4的大小为%s。'%(df3.shape,df4.shape))
print('内连接纵向合并后数据框大小为：',pd.concat([df3,df4],axis=0,join='inner').shape)
print('外连接纵向合并后数据框大小为：',pd.concat([df3,df4],axis=0,join='outer').shape)

# 使用append方法进行纵向表堆叠
print('append纵向堆叠后数据框大小为：',df3.append(df4).shape)

1.2 主键合并

  主键合并，即通过一个或多个键将两个数据集的行连接起来，类似于 SQL 中的 join。pandas 库中 merge 函数和 join 方法都可以实现主键合并，但是两者实现方式不同。
  和数据库的 join 一样，merge 函数也有左连接（left）、右连接（right）、内连接（inner）和外连接（outer）。但是使用 join 方法时，两个主键的名字必须相同。

DataFrame.merge(self, right, how='inner', on=None, left_on=None, right_on=None, left_index=False, 
			right_index=False, sort=False, suffixes=('_x', '_y'), copy=True, indicator=False, 
			validate=None)

merge 函数官方文档

merge 函数的常用参数说明

参数名称	说明
right	接收 DataFrame 或 Series。表示要添加的数据。
how	接收 inner、outer、left、right。表示数据的连接方式。默认为 inner。
on	接收 string 或 sequence。表示两个数据合并的主键（必须一致）。
left_on	表示左面数据用于合并的主键。
right_on	表示右面数据用于合并的主键。
suffixes	接收 tuple。表示用于追加左右两个数据框列名相同时的后缀。默认为 (’_x’, ‘_y’)

DataFrame.join(self, other, on=None, how='left', lsuffix='', rsuffix='', sort=False)

join 函数官方文档

join 函数的常用参数说明

参数名称	说明
other	接收 DataFrame 或 Series 或者多个 DataFrame 的 list。表示要连接的数据。
how	接收 inner、outer、left、right。表示数据的连接方式。默认为 left。
on	接收列名或者包含列名的 list 或者 tuple。表示用于连接的列名。
lsuffix	接收 string，表示用于追加左侧重叠列名的尾缀。无默认。
rsuffix	接收 string，表示用于追加右侧重叠列名的尾缀。无默认。

# 使用mrege函数合并数据表
order = pd.read_csv('meal_order_info.csv',encoding='gbk')
order['info_id'] = order['info_id'].astype('str')
detail_order = detail.merge(order,left_on='order_id',right_on='info_id')
print('detail订单详情表原始形状为：',detail.shape)
print('order订单信息表原始形状为：',order.shape)
print('两个表合并后的形状为：',detail_order.shape)

# 使用join方法实现主键合并
order.rename(columns={'info_id':'order_id'},inplace=True)
detail_order1 = detail.join(order.set_index('order_id'),on='order_id',lsuffix='_d',rsuffix='_o')
print('两个表合并后的形状为：',detail_order1.shape)

1.3 重叠合并

  数据分析和处理过程中偶尔会出现两份数据的内容几乎一致的情况，但是某些特征在其中一张表上是完整的，而在另一张表上的数据则是缺失的。这时除了使用将数据一对一比较，然后进行填充的方法外，还有一种方法就是重叠合并。pandas 提供 combine_first 方法来进行重叠合并。

DataFrame.combine_first(self, other)

combine_first 函数官方文档

# 重叠合并
df1 = pd.DataFrame({'A': [None, 0], 'B': [None, 4]})
df2 = pd.DataFrame({'A': [1, 1], 'B': [3, 3]})
print('df1：\n',df1)
print('df2：\n',df2)
print('df1与df2重叠合并后：\n',df1.combine_first(df2))  

df3 = pd.DataFrame({'A': [None, 0], 'B': [4, None]})
df4 = pd.DataFrame({'B': [3, 3], 'C': [1, 1]}, index=[1, 2])
print('df3：\n',df3)
print('df4：\n',df4)
print('df3与df4重叠合并后：\n',df3.combine_first(df4)) 

2. 清洗数据

  数据重复 会导致数据的方差变小，数据分布发生较大的变化；缺失值 会导致样本信息减少，不仅增加数据分析的难度，而且会导致数据分析结果产生偏差。异常值 则会产生 “伪回归”。因此需要对数据进行检测，查询是否有重复值、缺失值和异常值，并且要对这些数据进行适当的处理。

2.1 重复值

  常见的数据重复分为两种：一种为 记录重复，即一个或多个特征的某几条记录值完全相同；另一种为 特征重复，即存在一个或多个特征名称不同，但数据完全相同的情况。

2.1.1 记录重复

# 方法一：利用list去重（代码冗长，效率低，不推荐）
import pandas as pd

# 定义去重函数
def defRep(list1):
    list2=[]
    for i in list1:
        if i not in list2:
            list2.append(i)
    return list2

detail = pd.read_csv('detail.csv',encoding='gbk')
dishes = list(detail['dishes_name'])
print('去重前菜品总数为：',len(dishes))
dish = defRep(dishes)
print('方法一去重后菜品总数为：',len(dish))


# 方法二：利用set特性去重（代码简洁，但是数据排列会发生改变，不推荐）
print('去重前菜品总数为：',len(dishes))
dish_set = set(dishes)
print('方法二去重后菜品总数为：',len(dish_set))

  鉴于以上两种方法的缺陷，pandas 提供了 drop_duplicates 的去重方法。该方法只对 DataFrame 或者 Series 类型有效。这种方法不会改变数据的原始排列，并且代码简洁运行稳定。

DataFrame.drop_duplicates(self, subset=None, keep='first', inplace=False, ignore_index=False)

drop_duplicates 函数官方文档

drop_duplicates 方法常用参数说明

参数名	说明
subset	接收 string 或 sequence。表示进行去重的列。默认为 None，表示全部列。
keep	接收待定的 string。表示重复时保留第几个数据。first：保留第一个。last：保留最后一个。false：只要有重复都不保留。默认为 first。
inplace	接收 boolean。表示是否在原表进行操作。默认为 false。

# 使用drop_duplicates方法对菜品名称去重
dishes_name = detail['dishes_name'].drop_duplicates()
print('drop_duplicates方法去重后菜品总数为：',len(dishes_name))

# 使用drop_duplicates方法对多列去重
print('去重前订单详情表的形状为：',detail.shape)
shapeDet = detail.drop_duplicates(subset=['order_id','emp_id']).shape
print('依照订单编号、会员编号去重后订单详情表的大小为：',shapeDet)

2.1.2 特征重复

  要除去连续的特征重复，可以利用特征间的相似度将两个相似度为 1 的特征去除一个。在 pandas 中，相似度的计算方法为 corr。使用该方法计算相似度时，默认为 pearson 法，可以通过 method 参数调节，目前还支持 spearman 法和 kendall 法。
  但是通过相似度矩阵去重存在一个弊端，该方法只能对数值型特征去重，类别型特征之间无法通过计算相似系数来衡量相似度。

DataFrame.corr(self, method='pearson', min_periods=1) 

corr 函数官方文档
·

# 求出counts和amounts两列数据的Kendall法相似度矩阵
corrDet = detail[['counts','amounts']].corr(method='kendall')
print('销量和售价的Kendall法相似度矩阵为：\n',corrDet)

# 求出dishes_name、counts、amounts这三个特征的pearson法相似度矩阵
corrDet1 = detail[['dishes_name','counts','amounts']].corr(method='pearson')
print('菜品名称、销量和售价的pearson法相似度矩阵为：\n',corrDet1)

  除了使用相似度矩阵进行特征去重之外，还可以使用 DataFrame.equals 方法进行特征去重。

# 定义求取特征是否完全相同的矩阵函数
def FeatureEquals(df):
    dfEquals = pd.DataFrame([],columns=df.columns,index=df.columns)
    for i in df.columns:
        for j in df.columns:
            dfEquals.loc[i,j] = df.loc[:,i].equals(df.loc[:,j])
    return dfEquals

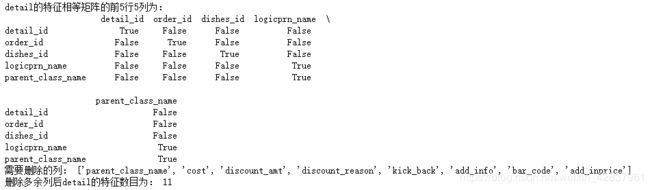
detEquals = FeatureEquals(detail)
print('detail的特征相等矩阵的前5行5列为：\n',detEquals.iloc[:5,:5])


# 通过遍历的方式进行数据筛选
lenDet = detEquals.shape[0]
dupCol = []
for i in range(lenDet):
    for j in range(i+1,lenDet):
        if detEquals.iloc[i,j] & (detEquals.columns[j] not in dupCol):
            dupCol.append(detEquals.columns[j])
            
print('需要删除的列：',dupCol)
detail.drop(dupCol,axis=1,inplace=True)
print('删除多余列后detail的特征数目为：',detail.shape[1])

2.2 缺失值

  数据中的某个或某些特征的值是不完整的，这些值称为缺失值。 pandas 提供了识别缺失值的方法 isnull 以及识别非缺失值的方法 notnull，这两种方法在使用时返回的都是 boolean 类型，即 True 和 False。结合 sum 函数和 isnull、notnull 函数，可以检测数据中缺失值的分布以及数据中一共含有多少缺失值。

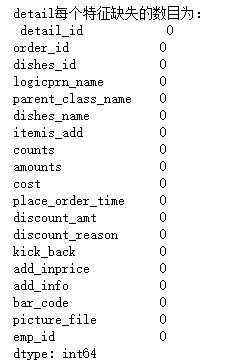
# isnull和notnull用法
print('detail每个特征缺失的数目为：\n',detail.isnull().sum())
print('detail每个特征非缺失的数目为：\n',detail.notnull().sum())

2.2.1 删除法

  删除法是指将含有缺失值的特征或者记录删除。删除法分为删除观测记录和删除特征两种，它属于通过减少样本量来换取信息完整度的一种方法，是一种最简单的缺失值处理方法。pandas 中提供删除缺失值的方法 dropna，通过参数控制，该方法既可以删除观测记录，也可以删除特征。

DataFrame.dropna(self, axis=0, how='any', thresh=None, subset=None, inplace=False)

dropna 函数官方文档

dropna 方法主要参数说明

参数名	说明
axis	接收 0 或 1。表示轴向。0 为删除行（记录），1 为删除列（特征）。默认为 0。
how	接收特定的 string。表示删除的形式。any：表示只要有缺失值存在就执行删除操作。all：表示当且仅当全部为缺失值时才执行删除操作。默认为 any。
subset	接收 array。表示进行操作的行/列。默认为 None，表示所有行/列。
inplace	接收 boolean。表示是否在原表上进行操作。默认为 False。

# 使用dropna方法删除缺失值
print('去除缺失的列前detail的形状为：',detail.shape)
print('去除缺失的列后detail的形状为：',detail.dropna(axis=1,how='any').shape)

2.2.2 替换法

  替换法是指用一个特定的值替换缺失值。特征可以分为数值型和类别型，两者出现缺失值时的处理方法不同。缺失值所在的特征为数值型时，通常利用其均值、中位数和众数等描述其集中趋势的统计量来替换缺失值；当缺失值所在的特征为类别型时，则选择使用众数来替换缺失值。pandas 提供了缺失值替换的方法 fillna。

DataFrame.fillna(self, value=None, method=None, axis=None, inplace=False, limit=None, downcast=None)

fillna 函数官方文档

fillna 方法主要参数说明

参数名	说明
value	表示用来替换缺失值的值。无默认。
method	接收特定 string。backfill 或 bfill：表示使用下一个非缺失值来代替缺失值。pad 或 ffill：表示使用上一个非缺失值来代替缺失值。默认为 None。
inplace	接收 boolean。表示是否在原表上进行操作。默认为 False。
limit	接收 int。表示填补缺失值个数上限，超过则不进行填补。默认为 None。

# 使用fillna方法替换缺失值
detail = detail.fillna(-99)
print('detail每个特征缺失的数目为：\n',detail.isnull().sum())

2.2.3 插值法

  删除法简单易行，但是会引起数据结构变动，样本减少；替换法使用难度较低，但是会影响数据的标准差，导致信息量变动。在面对数据缺失问题时，除了这两种方法，还有一种方法——插值法。
  常用的插值法有 线性插值、多项式插值 和 样条插值。线性插值是针对已知值求出线性方程，通过求解线性方程得到缺失值。多项式插值是利用已知值拟合一个多项式，使得现有数据满足这个多项式，再利用这个多项式求解缺失值。常见的多项式插值有拉格朗日插值和牛顿插值等。样条插值是以可变样条来做出一条经过一系列点的光滑曲线的插值方法。插值样条由一些多项式组成，每一个多项式都由相邻两个数据点决定，这样可以保证两个相邻多项式及其导数在连接处连续。
  pandas 提供了 interpolate 插值方法，能够进行上述部分插值操作，但是 SciPy 的 interpolate 模块更加全面。

scipy.interpolate 官方文档

# SciPi interpolate模块插值

# 线性插值
import numpy as np
from scipy.interpolate import interp1d      # 提示：这是数字1，不是字母l

x = np.array([1,2,3,4,5,8,9,10])             # 创建自变量x
y1 = np.array([2,8,18,32,50,128,162,200])    # 创建因变量y1
y2 = np.array([3,5,7,9,11,17,19,21])         # 创建因变量y2

LinearInsValue1 = interp1d(x,y1,kind='linear')   # 线性插值拟合x,y1
LinearInsValue2 = interp1d(x,y2,kind='linear')   # 线性插值拟合x,y2
print('当x为6、7时，使用线性插值y1为：',LinearInsValue1([6.,7]))
print('当x为6、7时，使用线性插值y2为：',LinearInsValue2([6.,7]))


# 拉格朗日插值
from scipy.interpolate import lagrange

LagInsValue1 = lagrange(x,y1)       # 拉格朗日插值拟合x,y1
LagInsValue2 = lagrange(x,y2)       # 拉格朗日插值拟合x,y2
print('当x为6、7时，使用拉格朗日插值y1为：',LagInsValue1([6.,7]))
print('当x为6、7时，使用拉格朗日插值y2为：',LagInsValue2([6.,7]))


# 样条插值
from scipy.interpolate import splev,splrep

SplineInsValue1 = splrep(x,y1)
SplineInsValue2 = splrep(x,y2)

print('当x为6、7时，使用样条插值y1为：',splev([6,7],SplineInsValue1))
print('当x为6、7时，使用样条插值y2为：',splev([6,7],SplineInsValue2))

  上面代码中，自变量 $x$ 和因变量 $y_1$的关系式为：$y_1=2x^2$ ；自变量 $x$ 和因变量 $y_2$的关系式为：$y_2=2x+1$
  从拟合的结果可以看出，多项式插值和样条插值在两种情况下的拟合都非常出色，线性插值法只在自变量和因变量为线性关系的情况下拟合才比较出色。而在实际分析过程中，自变量和因变量的关系是线性的情况非常少见，所以在大多数情况下，多项式插值和样条插值是比较合适的选择。

2.3 异常值

  异常值是指数据中个别值的数值明显偏离其余的数值，有时也称为离群点，检测异常值就是检验数据中是否有输入错误以及是否含有不合理的数据。异常值的存在对数据分析十分危险，如果计算分析过程中的数据中有异常值，那么会对结果产生不良影响，从而导致分析结果产生偏差乃至错误。常用的异常值检测主要为 3$\alpha$ 原则和箱线图分析两种方法。

2.3.1 3σ 原则

  3σ 原则又称为拉依达准则。该原则就是先假设一组检测数据只含有随机误差，对原始数据进行计算处理得到标准差，然后按一定的概率确定一个区间，认为误差超过这个区间就属于异常。不过，这种判别处理方法仅适用于对正态或近似正态分布的样本数据进行处理，而对其他分布类型的数据无效。

正态分布数据的 3α 原则

数值分布	在数据中占比
(μ-σ, μ+σ)	0.6827
(μ-2σ, μ+2σ)	0.9545
(μ-3σ, μ+3σ)	0.9973

  其中 σ 代表标准差，μ 代表均值。数据的数值分布几乎全部集中在区间 (μ-3σ, μ+3σ) 内，超出这个范围的数据仅占不到 0.3%。根据小概率原理，可以认定超出 3σ 的部分为异常数据。

# 使用3σ原则识别异常值

# 定义3σ原则识别异常值函数
def outRange(series):
    boolInd = (series < series.mean()-3*series.std()) | (series > series.mean()+3*series.std())
    index = np.arange(series.shape[0])[boolInd]
    outrange = series.iloc[index]
    return outrange

outRangeValue = outRange(detail['counts'])
print('使用3σ原则判定异常值个数为：',outRangeValue.shape[0])
print('异常值的最大值为：',outRangeValue.max())
print('异常值的最小值为：',outRangeValue.min())

2.3.2 箱线图分析

  箱线图提供了识别异常值的一个标准，即异常值通常被定义为小于 QL-1.5IQR 或大于 QU+1.5IQR 的值。其中，QL 称为下四分位数，表示全部观察值中有四分之一的数据取值比它小；QU 称为上四分位数，表示全部观察值中有四分之一的数据取值比它大；IQR 称为四分卫数的间距，是上四分位数 QU 与下四分位数 QL 之差，其间距包含了全部观察值的一半。

# 方法一：自定义箱线图函数识别异常值
import numpy as np

# 定义识别异常值函数
def outRange(series):
    QL = series.quantile(0.25)
    QU = series.quantile(0.75)
    IQR = QU - QL
    boolInd = (series>(QU+1.5*IQR)) | (series<(QL-1.5*IQR))
    index = np.arange(series.shape[0])[boolInd]
    outrange = series.iloc[index]  
    return outrange

outRangdeValue = outRange(detail['counts'])
print('使用箱线图判定异常值个数为：',outRangeValue.shape[0])
print('异常值的最大值为：',outRangeValue.max())
print('异常值的最小值为：',outRangeValue.min())


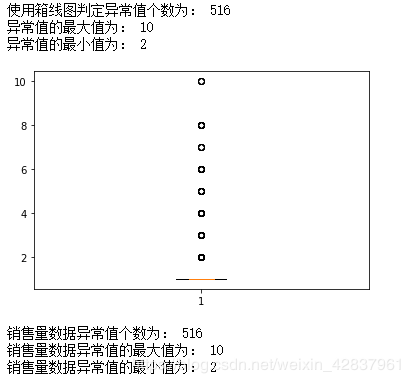
# 方法二：根据箱线图识别异常值
import matplotlib.pyplot as plt

p = plt.boxplot(detail['counts'].values,notch=True)
outRangeValue = p['fliers'][0].get_ydata()  # fliers为异常值的标签
plt.show()
print('销售量数据异常值个数为：',len(outRangeValue))
print('销售量数据异常值的最大值为：',max(outRangeValue))
print('销售量数据异常值的最小值为：',min(outRangeValue))

3. 标准化数据

  不同特征之间往往具有不同的量纲，由此所造成的数值间的差异可能很大，在涉及空间距离计算或梯度下降法等情况时，不对其进行数据处理会影响到数据分析结果的准确性。为了消除特征之间的量纲和取值范围差异可能会造成的影响，需要对数据进行标准化处理，也可以称作规范化处理。

3.1 离差标准化

  离差标准化是对原始数据的一种线性变换，结果是将原始数据的数值映射到 [0,1] 区间，转化公式如下：
$$X^{\ast }=\frac{X-min}{max-min}$$
  其中，$max$ 为样本数据的最大值，$min$ 为样本数据的最小值，$max-min$ 为极差。离差标准化保留了原始数据之间的联系，是消除量纲和数据取值范围影响最简单的方法。

# 离差标准化示例
import pandas as pd
import numpy as np

detail = pd.read_csv('detail.csv',encoding='gbk')

# 自定义离差标准化函数
def MinMaxScaler(data):
    return (data-data.min())/(data.max()-data.min())

# 对菜品订单表售价和销量做离差标准化
data1 = MinMaxScaler(detail['counts'])
data2 = MinMaxScaler(detail['amounts'])
data3 = pd.concat([data1,data2],axis=1)
print('离差标准化之前销量与售价数据的前5行为：\n',detail[['counts','amounts']].head())
print('离差标准化之后销量与售价数据的前5行为：\n',data3.head())

  离差标准化的缺点：若数据集中某个数值很大，则导致数据极差过大，使离差标准化的值会接近 0，并且相互间差别不大。

3.2 标准差标准化

  标准差标准化也叫零均值标准化或 $z$ 分数标准化，是当前使用最广泛的数据标准化方法。经过该方法处理的数据均值为 0，标准差为 1，转化公式如下：
$$X^{\ast }=\frac{X-\bar{X}}{\delta }$$
  其中，$\bar{X}$ 为原始数据的均值，$\delta$ 为原始数据的标准差。

# 标准差标准化示例
#自定义标准差标准化函数
def StandardScaler(data):
    return (data-data.mean())/data.std()

# 对菜品订单表售价和销量做标准化
data4 = StandardScaler(detail['counts'])
data5 = StandardScaler(detail['amounts'])
data6 = pd.concat([data4,data5],axis=1)
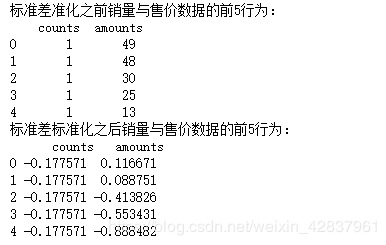
print('标准差准化之前销量与售价数据的前5行为：\n',detail[['counts','amounts']].head())
print('标准差标准化之后销量与售价数据的前5行为：\n',data6.head())

3.3 小数定标标准化

  通过移动数据的小数点位数，将数据映射到区间 [-1, 1]，移动的小数位数取决于数据绝对值的最大值。转化公式如下：
$$X^{\ast }=\frac{X}{{10}^k}$$

# 小数定标标准化示例
# 自定义小数定标标准化函数
def DecimalScaler(data):
    return data/10**np.ceil(np.log10(data.abs().max()))

# 对菜品订单表售价和销量做标准化
data7 = DecimalScaler(detail['counts'])
data8 = DecimalScaler(detail['amounts'])
data9 = pd.concat([data7,data8],axis=1)
print('小数定标标准化之前销量与售价数据的前5行为：\n',detail[['counts','amounts']].head())
print('小数定标标准化之后销量与售价数据的前5行为：\n',data9.head())

4. 转换数据

  数据分析的预处理工作除了数据合并、数据清洗以及数据标准化之外，还包括数据变换的过程。数据变换需要对数据做一些合理的转换，使之符合分析要求。

4.1 哑变量处理类别型数据

  数据分析模型中有相当一部分的算法模型都要求输入的特征为数值型，但实际数据中，特征的类型不一定只有数值型，还会存在相当一部分的类别型，这部分的特征需要经过哑变量处理才可以放入模型中。pandas 提供了 get_dummies 函数对类别型特征进行哑变量处理。

pandas.get_dummies(data, prefix=None, prefix_sep='_', dummy_na=False, columns=None, sparse=False, 
				drop_first=False, dtype=None) 

get_dummies 函数官方文档

get_dummies 函数常用参数说明

参数名称	说明
data	表示需要哑变量处理的数据。
prefix	表示哑变量量化后列名的前缀。默认为 None。
prefix_sep	接收 string。表示前缀的连接符。默认为 ’_‘。
columns	表示 DataFrame 中需要编码的列名。默认为 None，表示对所有 object 和 category 类型进行编码。

# 哑变量处理示例
import pandas as pd
import numpy as np

detail = pd.read_csv('detail.csv',encoding='gbk')
data = detail.loc[0:5,'dishes_name']   # 抽取部分数据做演示
print('哑变量处理前的数据为：\n',data)
print('哑变量处理后的数据为：\n',pd.get_dummies(data))

  对于一个类别型特征，若其取值有 m 个，则经过哑变量处理后就变成了 m 个二元特征，并且这些特征互斥，每次只有一个激活，这使得数据变得稀疏。由于数据变成了稀疏矩阵的形式，因此也加快了算法模型的运算速度。

4.2 离散化连续型数据

  某些模型算法，特别是某些分类算法，如 ID3 决策树和 Apriori 算法等，要求数据是离散的，此时就需要将连续型特征（数值型）变换成离散型特征（类别型），即连续特征离散化。
  连续特征的离散化就是在数据的取值范围内设定若干个离散的划分点，将取值范围划分为一些离散化区间，最后用不同的符号或整数值代表落在每个子区间中的数据值。因此离散化涉及两个子任务，即确定分类数以及如何将连续型数据映射到这些类别型数据上。
  常用的离散化方法主要有 3 种：等宽法、等频法 和 聚类分析法（一维）。

4.2.1 等宽法

  将数据的值域分为具有相同宽度的区间，区间的个数由数据本身的特点决定或者由用户指定，与制作频率分布表类似。pandas 提供了 cut 函数，可以进行连续型数据的等宽离散化。

pandas.cut(x, bins, right=True, labels=None, retbins=False, precision=3, include_lowest=False,
		duplicates='raise')

cut 函数官方文档

cut 函数常用参数说明

参数名称	说明
x	接收 array 或 Series。代表要进行离散化处理的数据
bins	接收 int、list、array 和 tuple。若为 int，则代表离散化后的类别数目；若为序列类型的数据，则表示进行切分的区间，每两个数的间隔为一个区间。无默认。
right	接收 boolean。代表右侧是否为闭区间。默认为 True。
labels	接收 list、array。代表离散化后各个类别的名称。默认为空
retbins	接收 boolean。代表是否返回区间标签。默认为 False。
precision	接收 int。显示标签的精度。默认为 3。

# 等宽法离散化示例
price = pd.cut(detail['amounts'],5)
print('离散化后5条记录售价分布为：\n',price.value_counts())

  缺陷：等宽法离散化对数据分布具有较高要求，若数据分布不均，那么各个类的数目也会变得非常不均匀，有些区间包含了许多数据，而另外一些区间的数据极少，这会严重损坏所建立的模型。

4.2.2 等频法

  cut 函数虽然不能够直接实现等频离散化，但是可以通过定义相同数量的记录放进每个区间。

# 等频法离散化示例
# 自定义等频法离散化函数
def SameRateCut(data,k):
    w = data.quantile(np.arange(0,1+1.0/k,1.0/k))
    data = pd.cut(data,w)
    return data

# 对菜品售价进行等频离散化
result = SameRateCut(detail['amounts'],5).value_counts()
print('菜品数据等频法离散化后各个类别数目分布状况为：\n',result)

  等频法离散化相较于等宽法离散化，避免了类分布不均的问题，但同时也有可能将数值非常接近的两个值分到不同的区间以满足每个区间对数据个数的要求。

4.2.3 聚类分析法

  一维聚类的方法包括两个步骤。首先将连续型数据用聚类算法（如 K-Means 算法等）进行聚类，然后处理聚类得到的簇，为合并到一个簇的连续型数据做同一种标记。聚类分析的离散化方法需要用户指定簇的个数，用来决定产生的区间数。

# 基于聚类分析的离散化
# 自定义数据K-Means聚类离散化函数
def KmeanCut(data,k):
    from sklearn.cluster import KMeans     # 引入K-Means
    
    kmodel = KMeans(n_clusters=k,n_jobs=4)         # 建立模型，n_jobs是并行数
    kmodel.fit(data.values.reshape(len(data),1))   # 训练模型
    c = pd.DataFrame(kmodel.cluster_centers_).sort_values(0)
    w = c.rolling(2).mean().iloc[1:]               # 相邻两项求中点，作为边界值
    w = [0]+list(w[0])+[data.max()]                # 把首末边界点加上
    data = pd.cut(data,w)
    return data

# 菜品售价聚类离散化
result = KmeanCut(detail['amounts'],5).value_counts()
print('菜品售价聚类离散化后各个类别数目分布状况：\n',result)

  K-Means 聚类分析的离散化方法可以很好地根据现有特征的数据分布状况进行聚类，但是由于 K-Means 算法本身的缺陷，用该方法进行离散化时依旧需要指定离散化后类别的数目。此时需要配合聚类算法评价方法，找出最优的聚类簇数目。