百度之星初赛（1）补题

有点懊悔，这是那天（7.19）被虐惨的第一场，到今天才补题。当初的flag似乎倒了呢，管他的，冲！
再也不在没做完的时候看榜了qwq，看了有什么用呢？还不如安心做题，悄悄拔尖。害！路走老了（不堪回首的往事又浮现眼前——拜托不要重蹈覆辙了），路走窄了。

第二题 GPA

传送门

小沃沃一共参加了 4 门考试，每门考试满分 100 分，最低 0 分，分数是整数。
给定四门考试的总分，请问在最优情况下，四门课绩点的和最高是多少？
分数与绩点之间的对应关系如下：
95~100 4.3
90~94 4.0
85~89 3.7
80~84 3.3
75~79 3.0
70~74 2.7
67~69 2.3
65~66 2.0
62~64 1.7
60~61 1.0
0~59 0

这题，通过率超高，我没做出来，有种被锤爆的感觉，一开始贪心，后来dp，全都WA，心态有点炸，根本没信心继续了。这种时候就要默默开始暴力啊，反正是混分，先暴力再说，看看原因，如果超时就头伸过来加个buff呗~害！真胆小，这种题目都不敢暴力，大不了四重循环嘛，每一重循环也就只有11次！瞅瞅把孩子吓的，多大个胆子！瞪大眼睛看清楚了啊，才这么点！

吓死宝宝了，那就暴力呗！

#include
using namespace std;

int gpa[11][2];		//11个挡位，左边分数右边GPA
double score;
int t;

int  main(){
	cin>>t;
	gpa[0][0] = 0, gpa[0][1] = 0;
	gpa[1][0] = 60, gpa[1][1] = 10;
	gpa[2][0] = 62, gpa[2][1] = 17;
	gpa[3][0] = 65, gpa[3][1] = 20;
	gpa[4][0] = 67, gpa[4][1] = 23;
	gpa[5][0] = 70, gpa[5][1] = 27;
	gpa[6][0] = 75, gpa[6][1] = 30;
	gpa[7][0] = 80, gpa[7][1] = 33;
	gpa[8][0] = 85, gpa[8][1] = 37;
	gpa[9][0] = 90, gpa[9][1] = 40;
	gpa[10][0] = 95, gpa[10][1] = 43;
	while (t--){
		cin>>score;
		int ans = 0;
		for (int i = 0; i < 11; ++i)
			for (int j = 0; j < 11; ++j)
				for (int k = 0; k < 11; ++k)
					for (int m = 0; m < 11; ++m){
						if(gpa[i][0] + gpa[j][0] + gpa[k][0] + gpa[m][0] <= score){
							if(gpa[i][1] + gpa[j][1] + gpa[k][1] + gpa[m][1] >= ans) ans = gpa[i][1] + gpa[j][1] + gpa[k][1] + gpa[m][1];
						}
					}
		cout<<ans / 10<<"."<<ans % 10<<endl;
	}
	return 0;			
}

好久没写这样的暴力了，颇有层次感。。但也不大，可以接受。qwq。

第三题 Dec

传送门
当时可以说极其烦躁，所以这题没有认真看，现在来——读题。

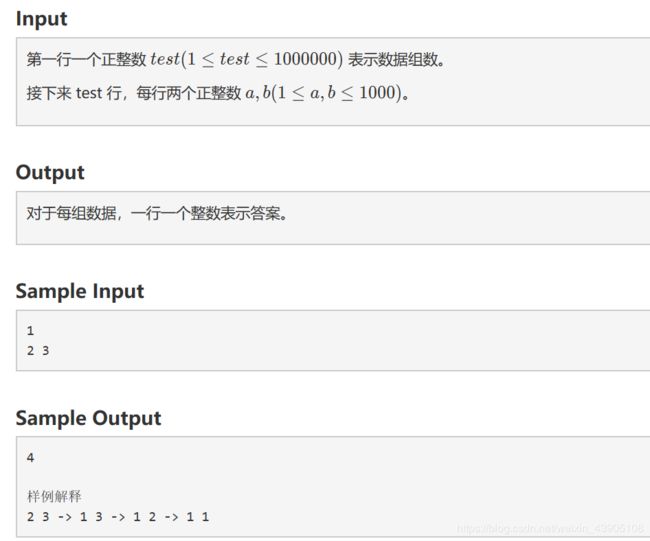
初始有 a,b 两个正整数，每次可以从中选一个大于 1 的数减 1，最后两个都会减到 1，我们想知道在过程中两个数互质的次数最多是多少。

看题10秒钟，好吧我承认没有思路，应该是数论题，但是我的数论功底还是太弱！
然鹅，很尴尬的是，这题看似是数论，实际上不是，应该是dp+打表。。。相当尴尬
思路如图：

然后顺带科普一下内联函数：

inline是C++关键字，在函数声明或定义中，函数返回类型前加上关键字inline，即可以把函数指定为内联函数。这样可以解决一些频繁调用的函数大量消耗栈空间（栈内存）的问题。关键字inline必须与函数定义放在一起才能使函数成为内联函数，仅仅将inline放在函数声明前面不起任何作用。inline是一种“用于实现”的关键字，而不是一种“用于声明”的关键字。

算了，还是套C++的壳子，写C的代码吧，不然感觉速度太慢了。

#include
#include
using namespace std;

const int N = 1e3+10;
int table[N][N];
inline int gcd(int x, int y){return x ? gcd(y % x, x) : y;}		//求最大公约数的内联函数
int t, m, n;

int main(){
	scanf("%d", &t);
	//开始写表
	for (int i = 1; i <= 1e3; ++i) table[1][i] = table[i][1] = i;
	for (int i = 2; i <= 1e3; ++i)
		for (int j = 2; j <= 1e3; ++j)
			table[i][j] = max(table[i - 1][j], table[i][j - 1]) + (gcd(i,j) == 1);
	while(t--){
		scanf("%d%d", &m, &n);
		printf("%d\n",table[m][n]);
	}
	return 0;
}

第四题 Civilization

传送门

这是一个回合制游戏，每一回合开始前会进行上一回合的结算。有一张 n∗n 的棋盘，我们出生在一个初始位置
(x,y)，现在我们要选择一个位置建设城市。你的人物每回合可以移动到距离你曼哈顿距离不超过 2 的位置，移动完成后可以选择是否建立城市。建立城市后，你的人物消失，成为一个人口为 1 的城市，这个人口要下回合才可以工作。如果不移动，直接在 (x,y) 建城，第 1 回合就可以开始工作。对于城市的每个居民，你可以安排他到距离城市曼哈顿距离小于等于 3 的位置进行工作，此居民可以瞬间到达该位置，每个位置最多安排一个居民，失业的人口不会生产任何食物。注意，城市位置上必须有一个居民在工作。结算按照如下顺序：当结算后城市总人口达到 9 游戏结束。
初始食物数量为 0，人口上涨不会导致之前积累的食物消失。输出最少几个回合能让游戏结束。

这题我就直接借鉴聚聚的思路了哈~我好像上午的时候连题目都没读懂，害！人家都做出来了。。。他求的最少回合数就=从每个点开始发展到9个居民的最少回合数（这里的最少是因为每发展一个居民都让他去曼哈顿距离<=3内的粮食最多的据点工作） + 从出发点到该点的回合数（这里求不了最小，因为每移动两个曼哈顿距离就需要一个回合）
不会还有的小可爱不知道曼哈顿距离吧，不会吧不会吧。。

这里膜拜带佬的码，我都注释了，就好理解多了——

#include
#include
using namespace std;
int a[505][505],x,y,n;      //数组a记录棋盘内容，(x,y)是起始坐标，n是棋盘大小
int ans[505][505];
int cot[5];
int minans;                 //max的作用
void BfsAndCalc(int x,int y)
{
    int cou=1,pro,round=0;
    cot[1]=cot[2]=cot[3]=cot[4]=0;
    for(int i=-3;i<4;i++)
    for(int j=-(3-abs(i));j<=3-(abs(i));j++)        //曼哈顿距离<=3
    {
        if(x+i>0&&x+i<=n&&y+j>0&&y+j<=n) cot[a[x+i][y+j]]++;        //看看周围在曼距<=3的范围内粮食储备从1-3的据点数量
    }
    cot[a[x][y]]--;     //自己所在的这个点不算，因为城中已有一人，不需掠夺
    pro=a[x][y]; //城内的粮食储备（每轮生产的食物）
    cot[4]=0;   //已经生产的食物
    while(cou!=9)
    {
        int temp=(8*cou*cou-cot[4]+pro-1)/pro;      //还要多少轮才能增加一个居民
        //这里(...+pro-1)/pro是为了向上取整，8*cou*cou哪怕只比cot[4]多一个也要算一轮
        round+=temp;cot[4]+=temp*pro;cou++;         //round统计总轮数，cot[4]统计总共增加的粮食，增加一个居民
        if(cot[3]!=0)
        {
            cot[3]--;pro+=3;    //从粮食多的地方开始掠夺，增加到自己的粮食储备里
        }else
        if(cot[2]!=0)
        {
            cot[2]--;pro+=2;    //储备为3的据点没有了，再找储备为2的据点
        }else
        if(cot[1]!=0)
        {
            cot[1]--;pro+=1;    //最后找储备为1的据点
        }
    }
    ans[x][y]=round;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        minans=1e9;
        scanf("%d%d%d",&n,&x,&y);
        for(int i=1;i<=n;i++)for(int j=1;j<=n;j++) scanf("%d",&a[i][j]);
        for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)
        {
            BfsAndCalc(i,j);
            if((abs(x-i)+abs(y-j)+1)/2+ans[i][j]<minans) minans=(abs(x-i)+abs(y-j)+1)/2+ans[i][j];
            //这里曼哈顿距离+1再除以2也是为了向上取整，哪怕曼哈顿距离为1也需要一个回合完成，除非为0
        }
        printf("%d\n",minans);
    }
    return 0;
}

参考内容：
2020 年百度之星·程序设计大赛 - 初赛一 题解

后面学扩展欧几里得。。数学鲨我嘤嘤嘤